Геометрическая и волновая сейсмика.

 

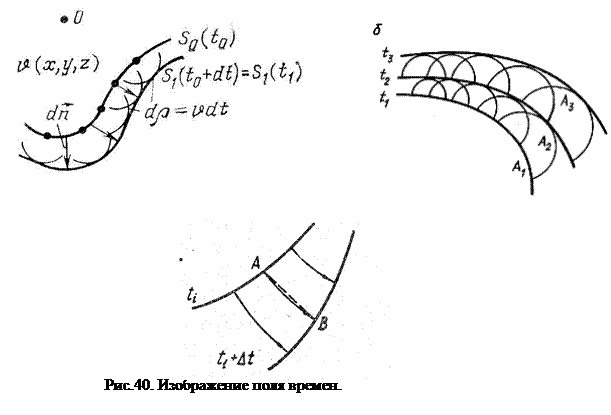
Как было показано выше, распространение упругих колебаний представляет собой волновой процесс. Пользуясь волновой теорией можно решать любые задачи распространения сейсмических волн в однородных и неоднородных в сейсмическом отношении средах. Однако, во многих важных практических задачах сейсморазведки более простые решения можно получить, используя лучевые представления геометрической сейсмики. Геометрическая сейсмика изучает законы распространения волн, основываясь на представлении об их фронтах и лучах. Свое название она получила по аналогии с геометрической оптикой, в которой введено понятие о световых лучах, и имеет общие с ней законы. Эти законы приемлемы только тогда, когда длина волны пренебрежимо мала в сравнении с протяженностью волнового фронта. Поскольку в реальной волновой сейсмике длина волны – величина конечная, то отступления от законов геометрической сейсмики тем меньше, чем больше размеры неоднородности, на которой волна образовалась.

В геометрической сейсмике есть несколько важных понятий, к которым часто прибегают в сейсморазведке. К ним относятся понятия изохроны и поля времен.

В сейсморазведке рассматриваются упругие волны, пробегающие расстояние во много раз больше, чем расстояние между тылом и передним фронтом. То есть можно допустить, что фронт и тыл неограниченно продолжаются, образуя так называемую волновую поверхность, а длина волны стремится к нулю. Положение волновой поверхности в пространстве в фиксированный момент времени называют изохроной. Пространство, охарактеризованное изохронами, то есть временами «прибытия» волны в различные точки этого пространства можно определить как поле времен. Изображая процесс распространения волн через лучи и изохроны, можно представить волновое поле как поле времен. Для описания процесса распространения волн в пространстве используют принцип Гюйгенса-Френеля и принцип Ферма.

Согласно принципу Гюйгенса-Френеля, каждый элемент упругой среды, пришедший в колебание, передает его соседнему элементу со скоростью, свойственной данному элементу, то есть, иными словами, сам становится источником колебаний.

Допустим, что нам известно положение изохроны в некоторый момент времени t₁ и значение скорости движения волны V. Допустим также, что эта скорость не меняется. Тогда можно построить сферические волновые поверхности элементарных волн, испускаемых элементами среды (частицами, пришедшими в колебание), лежащими на поверхности изохроны t. За время Δt из каждого такого элемента выйдет элементарная сферическая волна с радиусом поверхности r = v Δt, как показано на рис.40а.

	а

 

 

Огибающая всех этих волновых поверхностей дает нам положение изохроны реальной волны на момент t₂ = t₁ + Δt. Таким же образом можно построить изохроны t₃, t₄ и т.д., то есть построить поле времен, где любая точка пространства помимо координат отмечена временем прихода к ней упругой волны. Все эти изохроны будут конгруэнтны друг другу. Если скорость в среде меняется, то радиусы фронтов элементарной волны будут отличаться друг от друга. В случае, например, когда скорость не постоянная, а нарастает с глубиной по линейному закону V =V₀(1 + βz), где β – градиент нарастания скорости, изохроны будут расходиться с глубиной (рис.40б), а в случае убывания скорости - сходиться.

 

Скорость в каждой точке среды, называемая истинной скоростью, определяется как v(x,y,z) = lim(dn/dt), при dn → 0, а обратная величина

grad t = 1/v(x,y,z) называется градиентом поля времен.

Возведя это выражение в квадрат и расписав значение градиента по координатным осям, получим

(dt/dx)² + (dt/dy)² + (dt/dz)² = 1/v²(x,y,z)

Это дифференциальное уравнение является математическим выражением принципа Гюйгенса и называется уравнением поля времен, эйконала или уравнением Гамильтона. Для заданного распределения скоростей в среде оно позволяет определить конфигурацию волнового фронта для любого момента времени. Например, если среда однородная, то его решением будет выражение

t = √ x² +y² +z² /v, показывающее, что фронты волн в однородной среде представляют собой сферические поверхности.

Волновая поверхность перемещается в любой точке пространства вдоль нормали к ней, то есть вдоль сейсмических лучей. Для лучей справедлив принцип Ферма, согласно которому волна, распространяясь в пространстве, выбирает путь минимального времени пробега, то есть вариация времени (производная) по лучу равна 0.

Путь, кратчайший во времени между двумя точками А и В один и тот же, независимо от того, в каком направлении распространяется волна (рис.40в). Применение принципа Ферма, приводит к вывду, что в в однородной и изотропной среде лучи прямолинейны. В средах с изменяющейся скоростью лучи криволинейны и их форма определяется геометрически – построением линий, перпендикулярных фронтам (изохронам), или аналитически - криволинейным интегралом

t = ∫ds/v(x,y,z), где ds – элемент криволинейного луча. При вычислении интеграла требуется найти такой путь s(x,y,z), время пробега волны вдоль которого будет минимальным. Это уравнение является математическим выражением принципа Ферма.

Принцип Гюйгенса позволяет находить только положение фронта волны в любой момент, если задана скорость среде как функция координат ее точек. При этом отсутствует возможность решения динамической задачи – определения интенсивности влон, распространяющихся по разным направлениям. Этот недостаток устраняется дополнением принципа Гюйгенса идеей интерференции волн – тем самым ему придается волновая основа. Согласно модифицированному принципу Гюйгенса-Френеля, интенсивность упругой волны в любой точке среды за пределами ее волнового фронта определяется как результат интерференции элементарных сферических волн, источники которых равномерно распределены на волновой поверхности. Этот принцип обоснован для случая гармонических волн. Поле смещений равно сумме возмущений, создаваемых источниками в пределах малых кольцевых зон (Френеля). Полное поле смещений в какой либо рассматриваемой точке равно сумме смещений, создаваемых всеми зонами Френеля, на которые можно разбить волновую поверхность. При этом суммы колебаний, создаваемые по отдельности четными и нечетными зонами, равны и имеют противоположные фазы, вследствие чего взаимно ослабляют друг друга. Это приводит к тому, что результирующее возмущение, создаваемое всей сферической поверхностью, равно половине возмущения, создаваемого лишь первой зоной Френеля. Другими словами, наблюдаемое волновое поле в данной точке можно рассматривать как результат действия вторичных источников, расположенных во внутренней половине первой зоны Френеля. Реально радиус эффективной области среды, участвующей в передаче колебаний, будет равен

r_эф. ≈√bλ/2, где b – расстояние от рассмотриваемой точки до поверхности волнового фронта.

Теоретическим обобщением принципа Гюйгенса-Френеля является интеграл Кирхгофа, который является одним из решений волнового уравнения. Он позволяет найти значения поля смещений U(x,y,z,t) в произвольной точке P(x,y,z), находящейся во внешнем по отношению к некоторой замкнутой поверхности пространстве, если известны значения поля смещений U и его производных на этой поверхности (граничные условия)

 

U(x,y,z,t) = 1/4π ∫ ………………, где r - расстояние от точки P(x,y,z)

до точек поверхности интегрирования Q, v – скорость в однородной среде, n – направление нормали к поверхности. Значения в квадратных скобках берутся не для времени t, а для предшествующих моментов времени t`= t - r/v на поверхности Q.

Результирующее смещение в искомой точке зависит не от распределения на поверхности Q самих смещений, но и их производных по времени и по нормали к этой поверхности. Суммирование колебаний может происходить как в одинаковых, так и в противоположных фазах, соответственно, усиливая или ослабляя суммарный сигнал. Интегральная формула Кирхгофа- основа многих прямых и обратных решений динамических задач сейсморазведки для различных моделей сред, в частности, она является теоретической основой для получения сейсмических изображений. Точное решение задачи возможно, если известны граничные условия на поверхности Q. Невозможность получения точных граничных условий из сейсмоданных обусловливает приближенный характер решений на основе интеграла Кирхгофа.

Другой способ изучения распространения волнового поля от источников, в отличие от интегрального решения Кирхгофа, основан на последовательном пересчете поля с одного уровня на другой на основе численных решений волнового уравнения. Этот способ находит все большее применение в современной сейсморазведке и получил не вполне точное, но закрепившееся за ним название вычисления «на основе решения волнового уравнения».

Как уже говорилось, геометрическая сейсмика применима при рассмотрении различных явлений, когда длина волны пренебрежимо мала в сравнении с размером неоднородностей, на которых эта волна образовалась. Однако, встречается немало ситуаций, когда это условие не выполняется. С такими ситуациями, например, связано явление дифракции волн или интерференции иx на тонких слоях.

Под дифракцией в оптике понимают явление огибания препятствия световой волной. В сейсмике дифрагированная волна возникает и распространяется как волна рассеяния от элементов геологического разреза, на которых происходит изменение физических свойств пород – то есть возникает на любых неоднородностях среды. В реальных условиях дифрагированная волна устойчиво формируется и распространяется как самостоятельный тип колебаний, если размеры неоднородностей сопоставимы с длиной волны. Длины волны, с которыми имеют дело в сейсморазведке методом отраженных волн, колеблются в зависимости от скорости их распространения и от частоты (периода) колебания. Если положить, что отраженные волны, как правило, среднечастотны и, в основном, имеют периоды от 0,02 сек до 0,05 сек (то есть частотный их диапазон составляет 20-50 Гц), а скорости волн в осадочных толщах меняются в диапазоне от 2000 до 5000 м/сек, то получится, что длины волн измеряются величинами ~50-250 м. Это говорит о том, что появление дифрагированных волн наиболее вероятно на резких изгибах границ раздела, нарушениях сплошности пород (сбросах, надвигах, разломах), в зонах выклинивания. Пример возникновения и распространения дифрагированных волн для модели ступени (уступа) в рельефе отражающей границы приведен на рис. 41.

 

 

Рис.41. Дифракция сейсмической волны на ступени.

 

В области, примыкающей к источнику колебаний 0, регистрируются лучи ОВ. Так происходит, пока луч падающей волны не достигнет излома границы – точки дифракции Д. Согласно геометрическим представлениям на участке поверхности от крайнего луча ОВ₁ до луча ОВ₂, прошедших через точку дифракции никаких волн наблюдаться не будет, так как лучи падающей волны минуют уступ, попадающий в зону сейсмической тени.

Однако, согласно принципу Гюйгенса-Френеля частичка Д, пришедшая в колебание, начинает испускать элементарные волны, поверхности (фронты) которых огибают возникающие препятствия и заходят в зону сейсмической тени. Эти фронты достигают также поверхности наблюдений и попадают в промежуток между ОВ₁ и ОВ₂ и там их можно зарегистрировать. Понятно, что по интенсивности дифрагированные волны существенно слабее отраженных (~ в 2 раза), но во многих случаях этого вполне достаточно: такие волны регистрируются как признак наличия тектонических нарушений и т.п.

Без волновых представлений невозможно обойтись и при описании явлений, происходящих при отражении волн в случае тонкослоистого характера разреза.

Если длина волны соизмерима с толщиной слоя, то отражений от его кровли и подошвы на записи отделить невозможно. Это видно на рис. 42.

 

Рис. 42. Модель интерференции (а) и рефракции (б).

 

Промежуток времени ∆t, разделяющий импульсы отражений 1 и 2 окажется недостаточным для раздельной их регистрации сейсмоприемником: волна, отраженная от подошвы слоя подойдет раньше, чем отраженная от кровли завершит свою длительность и уйдет дальше. В итоге эти колебания наложатся друг на друга и прибор запишет длинное неразрешенное колебание. Это наложение волн и называют интерференцией. В случае, если волны складываются синфазно или запаздывание второй относительно первой кратно периоду колебания, интенсивность суммарной волны возрастает, а если суммирование происходит в противофазе (запаздывание кратно половине периода) колебания гасят друг друга. В итоге получаем характерные признаки интерференционной картины – многофазная неустойчивая динамика и т.д.

Из сказанного можно заключить, что геометрическая сейсмика неприменима в тех случаях, где приходится сталкиваться с ярко выраженной волновой природой колебаний. Таким образом, геометрическая сейсмика есть частный случай волновой, когда длина волны стремится к нулю (λ→0).

 

Рефракция волн.

 

Рассмотренные примеры образования и распространения волн относились к ситуациям, когда скорости в среде в целом, или в отдельных ее слоях не меняются. Однако, это далеко не так. Такие толщи как кристаллический фундамент в силу своей гетерогенности характеризуются сильной изменчивостью скорости. Довольно значительно меняются скорости в зависимости от глубины залегания в терригенных толщах, поскольку эти толщи в той или иной степени пористые, а пористость вследствие возрастающей геостатической нагрузки – то есть давления вышележащих пород –становится меньше и, соответственно, скорость больше. В таких средах, где скорость является непрерывной функцией координат пространства, в частности, глубины Z, прямолинейность лучей нарушается, они становятся криволинейными и возникает явление, именуемое рефракцией.

Пояснить природу этого явления можно таким примером (рис42б).Пусть среда представлена пачкой пластов, в каждой из которых скорость постоянная, но значения ее с глубиной растут, то есть V₁ < V₂ < V₃ …. И пусть по такой толще проходит упругая волна, представленная на рисунке лучом, вышедшим из источника под углом i₁. В соответствии с законом Снеллиуса, луч проходящей вниз волны будет, преломляясь, составлять с нормалью к границе постоянно возрастающие углы, все больше прижимаясь к горизонтали. Если устремить толщины слоев Δh к нулю, ломаная прямая выродится в непрерывную кривую, причем эта кривая в какой-то точке среды, пройдя через угол в 90°, повернет вверх и устремится к поверхности. Такой механизм возврата сейсмической энергии к поверхности наблюдений именуется рефракцией, а поворотная точка – точкой рефракции.

В наиболее сильной степени рефракция проявляет себя в ледовых толщах. В 60^х годах прошлого столетия, когда советские исследователи начали осваивать Антарктиду и одной из задач антарктических экспедиций стало изучение толщин материковых льдов этого континента, пришлось заняться обстоятельным изучением рефракции. Был разработан специальный метод рефрагированных волн, с помощью которого поставленные задачи удалось успешно решить.

Мы рассмотрели многочисленные (но не все) явления, происходящие в реальных средах при распространении волн и на основе этого рассмотрения можно заключить, что сейсмические импульсы по мере удаления от источника колебаний претерпевают значительные изменения – существенно уменьшается их интенсивность и изменяется форма (рис.43): если вблизи источника импульс короткий, высокочастотный, основная энергия сосредоточена в передних фазах колебаний (минимально-фазовый сигнал), то на значительном удалении амплитуда уменьшается, сигнал растягивается, становясь низкочастотным, а энергия перекачивается в хвостовые фазы колебаний.

 

 

	а
		б

 

 

Рис.43 Деформация сейсмического импульса в модели сплошной упругой среды:

а –вблизи источника, б-вдали от источника.

 

Заметно искривляются и траектории движения волн. Все это необходимо учитывать при выработке методики сейсморазведки для изучения достаточно глубоких горизонтов разреза.

Изложенные соображения справедливы, если представлять геологическую толщу в виде сплошной модели среды, причем исключительно пассивной, не порождающей собственных колебаний. Однако уже в конце ушедшего 20^го столетия, когда возникла и стала развиваться нелинейная динамика, появились новые представления и новые модели.

Новую модель среды легче представить, если вообразить, что хотя бы одно землетрясение уже когда-то произошло и речь идет о повторном возбуждении колебаний. Сплошность среды уже нарушена, есть трещины и микротрещины, есть куски, отдельности, флюиды, заполняющие эти трещины и все пустотное пространство породы- поры, содержащие газовую и жидкую фазы. Таким образом, новая модель представляет собой сложную систему, состоящую из блоков различных размеров, подчиняющихся определенной последовательности (по М.М.Садовскому (1989)). Система открыта, как и составляющие ее отдельности, для энергообмена с окружающей средой. Блоки в системе отделены друг от друга прослойками, сложенными из блоков разных размеров меньшего масштаба. Эта открытая система квазистационарна – в ней идут процессы перераспределения и трансформации энергии (и массы) поступающей извне. Она гетерогенна, энергонасыщенна и фрактальна (с элементами самоподобия упомянутых блоков). Она способна накапливать эту энергию и сохранять в себе некоторое ее количество (в том числе энергию упругих деформаций) в скрытом состоянии и после устранения непосредственных источников, бывших причиной ее появления. Энергонасыщенность проявляется в виде постоянно действующей сейсмической и акустической эмиссии, причем разные среды «звучат» по-своему. Распространение волн в такой среде характеризуется рядом особенностей: во-первых, низкочастотные сигналы могут вызывать высокочастотный отклик – расширение спектра идет в обе стороны, и форма записи может оказаться вовсе не такой, как показано на рис 43; во-вторых, слабый сигнал может вызывать сильный отклик; в-третьих, при взаимодействии гармонических волн появляются волны новых частот, кратных основным гармоникам – суммарным и разностным; в-четвертых, скорость волн зависит от амплитуды воздействия (Николаев,1994).

В спокойном состоянии, без «накачки», энергия внутренних напряжений находится в равновесном состоянии до достижения определенного уровня. При дополнительном возбуждении (воздействии внешним физическим полем) может произойти высвобождение накопленной энергии, которая, в том числе и в виде упругого поля, приведет к появлению колебаний, характеристики которых определяются физико-химическими свойствами среды (тела).

Если выделить эти колебания из общего волнового поля, то можно повысить достоверность прогноза залежей углеводородов. На новой модели основаны новые методы сейсморазведки, например, инфразвуковая сейсморазведка, разработанная саратовскими геофизиками.