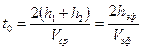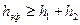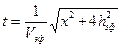Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особенности кинематики волн в средах с криволинейными границами раздела.Содержание книги
Поиск на нашем сайте
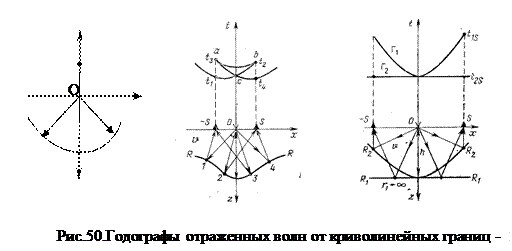
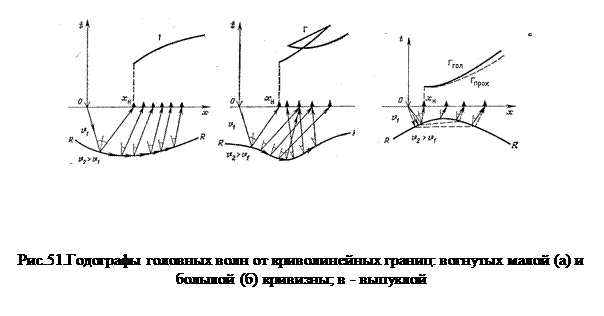
Выявленные особенности кинематики различных волн относились к моделям двухслойной среды с плоской границей раздела. Во многих случаях такое упрощенное представление о форме границ вполне приемлемо – например, при изучении осадочных толщ на платформенных территориях. Однако, при работах в межгорных депрессиях или даже в платформенных регионах, но с развитой солянокупольной тектоникой, то есть в районах, отличающихся криволинейностью отражающих и преломляющих поверхностей, кинематика волн существенно искажается. Рассмотрим простой пример. Пусть отражающая граница представляет собой элемент дуги окружности с центром на поверхности наблюдений и пусть в этом центре находится источник возбуждения колебаний. Нетрудно убедиться, что в этом случае лучи (если среда однородная) геометрически будут радиусами этой окружности и при отражении сфокусируются в точке возбуждения О. При этом годограф отраженной волны вырождается в точку (рис.50а). Если отражатель – окружность с центром – источником и этот источник находится на некоторой глубине под поверхностью наблюдений годограф ОВ будет представлять собой гиперболу, но с обратным соотношением абсцисс точек отражения и точек выхода лучей на поверхность: правая ветвь гиперболы будет отвечать левой стороне дуги отражательного элемента, а левая – правой, причем все отраженные лучи будут проходить через точку ПВ (центр окружности) – фокусироваться в ней. Эти простые примеры позволяют понять, что криволинейные формы синклинального (вогнутого) характера (в межкупольной мульде) на годографах ОВ проявляются вследствие подобной фокусировки как петли, точки возврата и крестообразные заходы (рис 50а), причем донышко петли будет представлять собой донышко мульды, ее правая ветка после креста-пересечения соответствовать левому склону, а левая ветка правому склону; точки возврата а и b - это точки смены характера соответствия (прямого на обратное) упомянутых абсцисс точек отражения точкам выхода луча. В свою очередь на отражательных элементах выпуклого характера (куполах) будет отмечаться не фокусировка, а напротив, аномальное расхождение лучей. Если отражающий элемент имеет форму параболического зеркала, отраженные лучи становятся параллельными, а пути – одинаковыми. Годограф Г2 превращается в горизонтальную прямую t = const (рис.50в).
Годограф преломленной волны также искривляется (рис.51 а и 51 б), а в случае выпуклой границы на записях МПВ в первых вступлениях могут быть зарегистрированы не головные, а проникающие вглубь дважды преломленные волны, бегущие в подстилающей толще с высокой скоростью V2, но не вдоль дуги, а по ее прямолинейной хорде, то есть по более короткому пути. Этот эффект носит название эффекта проницания 1го рода (рис.51в).
.
Годографы ОВ в слоистой среде. Понятие Vэф.
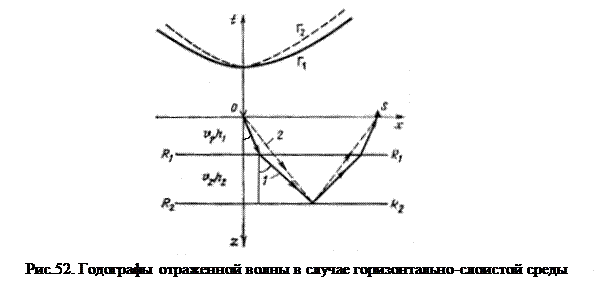
Еще одно упрощение нашей модели, с которым придется распрощаться, стремясь приблизиться к объективной реальности – это ее двухслойный характер. Реальные среды многослойные. В многослойной среде каждый падающий и отраженный лучи преломляются на промежуточных границах в соответствии с законом Снеллиуса. Рассмотрим вновь самый простой пример многослойной среды, когда покрывающая разведуемую границу R2 среда состоит из двух слоев мощностью h1 и h2 со скоростями V1 и V2 (рис. 52). Уравнения линейного продольного годографа отраженной волны для такой модели можно записать в параметрической форме для произвольного луча, выходящего из источника под углом α1:
При замене х на –х и α на –α правые части в приведенных уравнениях не изменятся, то есть годограф будет представлять собой симметричную относительно оси t функцию. В точке х=0, V*=∞ (вертикальный подход волны), при возрастании х - V* монотонно убывает. Все это говорит о безусловном сходстве зависимости t от х с гиперболической, установленной для двухслойной модели. В то же время, строгое исследование показывает, что это не гипербола, а более пологая кривая, которая ближе всего к параболе с минимумом в точке х=0 (при горизонтальном залегании границ). Попробуем сопоставить рассматриваемый годограф с годографом отраженной волны от той же границы R2 , но с заменой слоистой среды на однородную со средней скоростью Vср (пунктирная кривая на рис. 52), причем это не арифметическое среднее из V 1 и V2, а более сложная функция, определяемая как частное от деления общего пути, пройденного волной на общее время, затраченное ею на этот пробег. Причем имеется в виду пробег по центральному лучу, то есть по нормали к границе
Такую скорость можно найти при наблюдениях во внутренних точках среды (в скважине), проведя специальный вид исследований в скважине, называемый сейсмокаротажом. Очевидно, что в точке х=0 времена по обоим годографам совпадают, то есть
Понятно также, что теоретический годограф с параметром Vср будет представлять собой гиперболу (поскольку слоистая среда заменена однородной и трехслойная модель тем самым трансформирована в двухслойную). По мере увеличения расстояния х возрастет разность времен сопоставляемых годографов(волна стремится пройти больший путь со скоростью V2), причем годограф, полученный с учетом слоистости (на рис 30 – непрерывная кривая) располагается ниже пунктирной теоретической кривой для однородной среды. Различие времен годографов тем больше, чем больше отклонение действительных падающего и отраженного лучей от прямолинейных отрезков, что зависит от соотношения скоростей V1/V2, толщин h1/h2 и расстояния х. Такая закономерность выдерживается для всех горизонтально слоистых сред, независимо от характера чередования пластов. Это следует из принципа Ферма: действительно, путь по ломаной прямой удовлетворяет принципу минимума времени. Таким образом все годографы ОВ при небольшой протяженности (в сравнении с глубиной исследуемой границы)трактуются как гиперболы - в области, примыкающей к ПВ, годограф Г2 может быть аппроксимирован гиперболической (эффективной) кривой, совпадающей с Г2 в пределах определенной погрешности. То есть реальный годограф может быть «заменен» годографом волны, как бы отраженной от границы на глубине Hэф(эффективная глубина), покрытой однородной средой Vэф(эффективная скорость).
где Vэф – параметр эффективной гиперболы. Таким образом, по наблюденному годографу может быть вычислена скорость Vэф по приведенной формуле в предположении, что этот годограф – гипербола. Очевидно, что Vэф≥ Vср. Различие мало вблизи ПВ и когда отношение этих скоростей мало отличается от единицы (среда, недифференцированная по скорости).
Так как Vэф≥ Vср, значит и
Возможности определения скоростной характеристики среды в виде Vэф и реальная близость последней к Vср является чрезвычайно важным в практическом отношении достоинством сейсморазведки и выгодно отличает ее от других методов геофизики, где такие возможности отсутствуют. Действительно, по полевым данным одной только гравиразведки нельзя определить плотность, по магнитным – магнитную восприимчивость и намагниченность и пр. С помощью изложенного подхода, то есть, подставляя в гиперболическое уравнение реальные времена с наблюденного годографа, мы последовательно определим эффективные (средние) скорости для всей толщи, покрывающей каждую следующую отражающую границу. А по скоростям и времени получим возможность оценить структурные конфигурации отражающих границ и выявить в их рельефе объекты поиска. Необходимо отметить, что с увеличением глубины залегания границ мы будем наблюдать уменьшение крутизны годографов, отраженных от них волн, их последовательное выполаживание – приближение к форме самой границы отражения.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 656; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.3.198 (0.011 с.) |

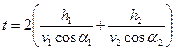 ;
;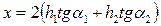
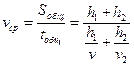
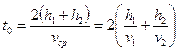
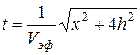 ,
,