
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Важнейшее свойство потенциала.Содержание книги
Поиск на нашем сайте Зададимся вопросом: как выглядит распределение потенциала на поверхности, в любой точке которой g направлено по нормали к этой поверхности, то есть S Из всего мыслимого множества уровенных поверхностей, отвечающих уравнению W=C (C1,C2,C3 –различные значения постоянной соответствуют различным уровенным поверхностям) есть одна, которая существует физически, которую можно «потрогать». Это поверхность невозмущенной никакими горизонтальными (тангенциальными) силами (например, силой ветра) морей и океанов. Будучи мысленно продолженной под континенты она обрисует фигуру Земли, которую называют геоид. Именно геоид принимают за фигуру Земли в геологии, во всех геологических науках, кроме гравиразведки. В гравиразведке, как уже говорилось выше, за фигуру Земли, за ее модель принимают сфероид. Чем они отличаются? Геоид – это эквипотенциальная поверхность реальной вращающейся Земли, тогда как сфероид – эквипотенциальная поверхность воображаемой (модель) вращающейся Земли, у которой все горы выровнены, а моря заполнены на одинаковую глубину. При этом ее масса и объем остаются такими же, как у реальной Земли [4 ]. Почему же гравиметристов не устраивает в качестве модели геоид, а устраивает только сфероид? Дело в том, что геоид это поверхность не идеальная, а ундулирующая. Ундуляции или местные возмущения возникают под действием физических неоднородностей земной коры и топорельефа местности. На рис.4 видно, что из-за притяжения «избытков» масс (например, горных массивов краевых зон континентов) отвес отклоняется в сторону этих масс, а показанная пунктиром уровенная поверхность (всегда перпендикулярная вектору g, который как раз и определяет нить отвеса) образует, таким образом «положительную» ундуляцию (вздымается). Над океаном из-за недостатка масс образуется отрицательная ундуляция.
Рис.4.Ундуляции геоида.
Срезающая эти ундуляции на рис.4 сплошная кривая дает представление об осредненном невозмущенном положении геоида. Такой геоид называют эллипсоидом относимости. Трехосный эллипсоид - это более близкое, чем сфероид приближение к истинной фигуре Земли, поскольку у нашей планеты различаются не только полюсной и экваториальный радиусы. Если рассмотреть само экваториальное сечение, то оно на самом деле окажется не идеальным кругом. Два главных радиуса этого сечения буду различаться примерно на 200 м. В сравнении с различием полюсного и экваториального радиусов, разница между которыми составляет ~21 км, это всего лишь 1%, и тем не менее, эллипсоид – это более точное представление фигуры Земли. Поэтому в большой геофизике именно эллипсоид определяет эту фигуру, но для гравиразведки вполне годится в качестве модели сфероид. Сфероид – это поверхность практически идеальная, близкая к среднему невозмущенному положению геоида и для такой поверхности нетрудно вычислить нормальное поле g0, которое необходимо для получения имеющих геологический смысл аномальных значений Δgа. В целом поверхность земного сфероида незначительно отклоняется от поверхности геоида на морях и океанах – максимум на ±150м.
Градиенты силы тяжести
Сама по себе величина потенциала W непосредственно не измеряется. Измерению подлежат только первые производные Wz, то есть составляющие g, в частности g(z) и вторые производные потенциала Wzx и Wzy, именуемые градиентами силы тяжести
Вторые производные Wzx и Wzy характеризуют скорость изменения gz (то есть ее градиент) по горизонтали (в плоскости XOY, касательной к поверхности) и имеют размерность Вертикальный градиент позволяет оценить, как меняется сила тяжести с изменением высоты точки наблюдения относительно уровня моря, то есть поверхности сфероида (геоида). Из всех градиентов вертикальный имеет наибольшую величину, которая составляет примерно 3·10-6 1/с2. За единицу измерения градиентов силы тяжести принимается этвеш (Е). Один Е соответствует изменению силы тяжести на 0,1 мГал на участке в 1 км. Таким образом 1 Е=1·10-91/сек2. Название этвеш связано с именем венгерского физика Этвеша, который изобрел специальный прибор для измерения градиентов – гравитационный вариометр, действующий по принципу крутильных весов Кулона. В наше время вариометрические съемки проводятся сравнительно редко, в основном в рудной геофизике
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 510; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.40.151 (0.009 с.) |

 g. В этом случае cos(g,s)=0 и, соответственно,
g. В этом случае cos(g,s)=0 и, соответственно,  = 0, а W=const (W =C). Такая поверхность, в любой точке которой сила тяжести (притяжения) направлена к ней нормально, а потенциал W(U) имеет постоянное значение, называется поверхностью равного потенциала или уровенной поверхностью. На такую поверхность действует только нормальная (вертикальная) составляющая g (то есть gz). На такой поверхности устанавливается – не течет – жидкость в сосуде (если пренебречь силой поверхностного натяжения).
= 0, а W=const (W =C). Такая поверхность, в любой точке которой сила тяжести (притяжения) направлена к ней нормально, а потенциал W(U) имеет постоянное значение, называется поверхностью равного потенциала или уровенной поверхностью. На такую поверхность действует только нормальная (вертикальная) составляющая g (то есть gz). На такой поверхности устанавливается – не течет – жидкость в сосуде (если пренебречь силой поверхностного натяжения).


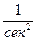 . Их называют горизонтальными градиентами силы тяжести, в отличие от вертикального Wzz =
. Их называют горизонтальными градиентами силы тяжести, в отличие от вертикального Wzz =  =
=  = dg /dz. Именно горизонтальные градиенты имеют геологический смысл, поскольку над относительно небольшими телами, зачастую почти не проявляющими себя в поле Δgа , наблюдаются аномалии Wzx и Wzy.
= dg /dz. Именно горизонтальные градиенты имеют геологический смысл, поскольку над относительно небольшими телами, зачастую почти не проявляющими себя в поле Δgа , наблюдаются аномалии Wzx и Wzy.


