
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деформации и напряжения. Упругие коэффициенты.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Деформации объема удобно рассмотреть на примере модели линейного элемента (ребро параллелепипеда), то есть тела, имеющего только один размер. Физически такое тело можно представить в виде длинного и узкого стержня, поперечный размер которого пренебрежимо мал в сравнении с длиной. Закрепим такой стержень верхним торцом, а к противоположному концу приложим растягивающую нагрузку (силу) - F (рис 36).
В результате приложения этой силы частички сместятся. Обозначим вектор смещения через Возьмем теперь разность смещений и отнесем ее к разности удалений - По физическому смыслу это есть относительное удлинение линейного элемента, его деформация, которую мы обозначим как exx. Теперь возьмем векторную сумму
Составляющая этого вектора Рx будет связана с деформацией exx линейной зависимостью, называемой законом Гука: величина деформации прямо пропорциональна величине приложенного напряжения (вскользь этот закон уже упоминался в лекции по гравиразведке). Этому закону подчиняются упругие среды. Понятно, что геологические среды поведут себя как упругие только тогда, когда напряжения будут невелики и весьма кратковременны (как известно, геологические среды при длительно прилагаемых нагрузках деформируются пластически, «текут», изгибаются в складки без разрыва сплошности, а если напряжения велики, то с разрывом – сбросы, надвиги). Закон Гука может быть записан в виде соотношения
отсюда
Коэффициент пропорциональности между напряжением и деформацией обозначим через Е. Этот упругий коэффициент носит название модуль Юнга или коэффициент продольного растяжения. По физическому смыслу Е – это сила, которую надо приложить, чтобы произошло удлинение стержня, равное единице длины, то есть одному метру. Размерность Е, как это видно из приведенного соотношения, совпадает с размерностью напряжения Р, поскольку exx – относительная (безразмерная) величина. То есть размерность Е - Еще один упругий коэффициент, смысл которого может быть уяснен из приведенной модели, носит название коэффициента поперечного сжатия, или коэффициента Пуассона, обозначаемого греческой буквой ν (ню). Он представляет собой отношение относительного сжатия стержня δy/y к относительному удлинению δx/x
Понятно, что в результате приложения растягивающей нагрузки стержень удлинится на δх (по отношению к первоначальной длине х) и станет уже на δy (по отношению к первоначальной длине y). Понятно также, что ν – безразмерная величина и, как правило, очень маленькая. Для подавляющего большинства горных пород ν близко к 0,25 и только для очень рыхлых пород ВЧР (верхней части разреза) приближается к 1. Коэффициент Пуассона можно также записать в виде соотношения ν = - e yy/ e xx, где e yy – относительное растяжение по оси y, а e xx – относительное сжатие по оси x. Через линейные элементы (точнее, через относительные удлинения всех сторон объемного тела – параллелепипеда, который легко описать тремя линейными элементами, исходящими из одной точки – вершины: длина х, ширина у, высота z) может быть найдено изменение всего этого малого объема, его объемное расширение, или кубическая дилатация Θ
Из приведенной записи хорошо видно, что это математическая операция с вектором смещения
Модель сдвиговой деформации представлена на рис.37 на примере грани рассматриваемого параллелепипеда, одна сторона которой закреплена, а к противоположной приложена внешняя сила F.
Рис.37. Сдвиговая деформация.
Тогда понятно, что частички из ряда, удаленного от начала координат на расстояние х получит смещение v (составляющая вектора
Сама эта деформация, которую можно также записать в виде e yx выразится в сдвиге сторон или в скошении γ прямого угла, точнее, она будет представлять собой тангенс этого угла, но для малых углов, как известно tgγ ≈ γ. Если закрепить другую грань (по оси х) и приложить в направлении х внешнюю нагрузку к противоположной грани, то получим аналогичное скошение Суммарное скошение (e yx + e xy), если закрепить грань только в одной верхней угловой точке и приложении одинаковых касательных сил к двум сторонам грани, как показано на рис. 37, определяется как При неравенстве сил, прикладываемых к граням, кроме сдвиговых возникают вращательные компоненты деформации, представляемые в виде разности сдвиговых компонент
Аналогичным образом можно записать выражения для других пар ωxz и ωxz. В результате действия сдвиговых компонент изменяется форма исходного объема, поэтому такая деформация называется деформацией формы.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 559; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.29.202 (0.009 с.) |


 , а его составляющие по осям координат через u, v и ω соответственно. В рассматриваемом случае можно учитывать только составляющую u, пренебрегая остальными. Обозначим смещение, полученное частичками, отстоящими от закрепленного конца стержня на расстояние х через u. Вследствие действия сил сцепления между частичками, составляющими стержень (сил межчастичного взаимодействия, пружинок),– смещения будут тем меньше, чем ближе к закрепленному концу стержня они находятся. Это значит, что более удаленные частички, то есть х + Δх получат большее смещение, то есть u +Δu.
, а его составляющие по осям координат через u, v и ω соответственно. В рассматриваемом случае можно учитывать только составляющую u, пренебрегая остальными. Обозначим смещение, полученное частичками, отстоящими от закрепленного конца стержня на расстояние х через u. Вследствие действия сил сцепления между частичками, составляющими стержень (сил межчастичного взаимодействия, пружинок),– смещения будут тем меньше, чем ближе к закрепленному концу стержня они находятся. Это значит, что более удаленные частички, то есть х + Δх получат большее смещение, то есть u +Δu. . Если устремить Δх к нулю и взять предел этого отношения, то перейдем от бесконечно малых к производной
. Если устремить Δх к нулю и взять предел этого отношения, то перейдем от бесконечно малых к производной  .
.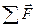 всех сил, действующих на свободный торец стержня и отнесем ее к площади его поперечного сечения S –получим величину приложенного напряжения, которое обозначим через Р
всех сил, действующих на свободный торец стержня и отнесем ее к площади его поперечного сечения S –получим величину приложенного напряжения, которое обозначим через Р
 ,
,
 (ньютон на метр в квадрате). Вполне понятно, поскольку растянуть линейный элемент на метр исключительно тяжело, что сами по себе величины Е очень велики. Так, для осадочных пород значения Е заключены в диапазон от 0,05·1010 до 10·1010н/м2, для кристаллических диапазон у'же и сами значения выше - от 3·1010 до 20·1010н/м2, для воды 2·1010н/м2.
(ньютон на метр в квадрате). Вполне понятно, поскольку растянуть линейный элемент на метр исключительно тяжело, что сами по себе величины Е очень велики. Так, для осадочных пород значения Е заключены в диапазон от 0,05·1010 до 10·1010н/м2, для кристаллических диапазон у'же и сами значения выше - от 3·1010 до 20·1010н/м2, для воды 2·1010н/м2.





 ., или e xy
., или e xy , где Рху – составляющая тангенцильного напряжения, а μ – коэффициент пропорциональности между напряжением и деформацией, называемой модулем сдвига. Таким образом, видно, что при касательных напряжениях происходит изменение формы первоначальных объемов – деформация формы (или сдвига частичек одного ряда относительно другого или перекосы).
, где Рху – составляющая тангенцильного напряжения, а μ – коэффициент пропорциональности между напряжением и деформацией, называемой модулем сдвига. Таким образом, видно, что при касательных напряжениях происходит изменение формы первоначальных объемов – деформация формы (или сдвига частичек одного ряда относительно другого или перекосы).


