
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особенности годографов ПВ в случае горизонтально слоистой среды.Содержание книги
Поиск на нашем сайте
Применительно к такой модели условие образования преломленных волн V2 > V1 следует, казалось бы, переписать в виде Из закона Снеллиуса следует, что Отсюда можно записать, что Таким образом, необходимо, чтобы и V1, и V2 были меньше V3, а в случае с многослойными моделями с n слоями Vn > Vк для любых к < n. Серию годографов преломленных волн для многослойной модели среды с последовательно возрастающими скоростями можно видеть на рис. 56.
Эта серия представляет собой ломаную прямую, образованную пересекающимися прямолинейными (поскольку преломляющие границы плоские) отрезками, каждый из которых соответствует выходу в первые вступления очередной преломленной волны. С возрастанием глубины границы область выхода волны в первые вступления все больше удаляется от источника. В учебной литературе можно познакомиться с особенностями других волн (дифрагированных, кратных и т.п.) и убедиться, что все они характеризуются различной кинематикой, то есть их годографы отличаются друг от друга. Кинематические особенности кратных волн
Упомянутые отличия наблюдаются тогда, когда скорости с глубиной возрастают (как это обычно бывает). Соотношение годографов кратных и однократных волн в системе ОТВ для случая, когда отражающие границы залегают горизонтально можно видеть на рис58.
Заметим, что волна первой кратности от глубокой границы (II) может регистрироваться одновременно с волной второй кратности от первой границы (I), но у однократной годограф положе, то есть V* больше. Различия тем более заметны, чем дальше по х отойти от ПВ. В случае наклонной границы минимумы гипербол смещается в сторону восстания, причем для кратных эти смещения больше.
Аналитические различия таковы: уравнение годографа волны первой кратности от первой границы
Смещения минимумов: для однократной - h/Sin φ, двукратной – h2/Sin2φ, m-кратной – hm/Sin(m φ) Для волны первой кратности от второй границы уравнение времени по своей структуре будет таким же как t1(1) , но с заменой V на Vэф и H на Н эф. В системе ОГТ годографы кратно-отраженных волн имеют форму гипербол, вершины которых расположены в точке ОСТ (ЦБ), а кривизна определяется параметром VmОГТ= V/cos(mφ) Кривизны гиперболических годографов (или близких кривых) на сейсмограммах ОГТ различны. Годографы кратных волн, как правило, имеют большую кривизну, чем однократных. Это обусловлено тем, что скорости с глубиной возрастают и получается, что кратные отражения совершают свой пробег в относительно низкоскоростной среде. Таким образом, только на сейсмограммах ОГТ все рассиотренные волны имеют годографы (в основном, гиперболы) симметричные относительно ОСТ (ЦБ). Различие волн на сейсмограммах ОГТвыражается только в разной кривизне их годографов. Это обстоятельство используется в методе ОГТ. Тем не менее, в целом такая форма отображения геологии как годограф далека от реальности. Кроме этого, нельзя не отметить, что годографы сильно искажаются влиянием верхней части разреза – рельефом местности, изменчивостью ЗМС и пр. Куда более удобной с точки зрения геологического прочтения сейсмической информации формой ее представления является временной разрез. Для получения временного разреза из совокупности сейсмограмм необходимо ввести в записи специальные поправки.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 778; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.134.140 (0.009 с.) |

 . Но теперь это условие необходимое, но не достаточное. Оно может быть выполнено только при определенном соотношении между V1, V2 и V3.
. Но теперь это условие необходимое, но не достаточное. Оно может быть выполнено только при определенном соотношении между V1, V2 и V3. .
.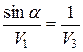 . То есть
. То есть 

 Каковы особенности кратных волн? По динамике они мало отличаются от однократных – могут быть и более высокочастотными и более низкочастотными и такими же. По кинематике отличия есть, но не такие существенные, как для поверхностных волн. Кратные волны – это, как уже говорилось, волны, испытавшие не один акт отражения от одной границы. Причем схемы распространения кратных волн могут быть самые различные (рис.44)
Каковы особенности кратных волн? По динамике они мало отличаются от однократных – могут быть и более высокочастотными и более низкочастотными и такими же. По кинематике отличия есть, но не такие существенные, как для поверхностных волн. Кратные волны – это, как уже говорилось, волны, испытавшие не один акт отражения от одной границы. Причем схемы распространения кратных волн могут быть самые различные (рис.44) , а волны второй кратности от нее же
, а волны второй кратности от нее же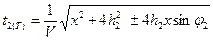 , где h2= 2hcosφ; φ2=2φ. Обобщая на случай n границ получим hn=h
, где h2= 2hcosφ; φ2=2φ. Обобщая на случай n границ получим hn=h  ; φn= nφ.
; φn= nφ.


