Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение Шредингера. Физический смысл волновой функции.
Основным уравнением квантовой механики является уравнение Шредингера. Оно сформулировалось в результате анализа большого числа экспериментальных фактов. Справедливость уравнения доказывается тем, что все вытекающие последствия точно согласованы с опытными фактами. Уравнение Шредингера: - особое уравнение, которое сочетает в себе как волновые, так и корпускулярные свойства частиц - записано в 1928 году Э. Шредингером. Взаимодействие частиц с силовым полем задает потенциальная энергия U(x,y,z,t), которая в общем случае зависит от координат частицы и от времени. Волновые свойства микрочастиц определяет так называемая «пси»-функция Корпускулярные свойства микрочастиц определяет ее масса – m. Состояние микрочастиц: Стационарное – ее потенциальная энергия не зависит от времени и является функцией только координат.
Из уравнения Шредингера => что вид -функции определяется потенциальной энергией, то есть действием сил на частицу (характером). Нестационарное – потенциальная энергия зависит от времени и от координат.
Таким образом, распадается на 2 уравнения: 1) После интегрирования: После потенцирования: 2) Для нахождения координат частицы
Решение этого уравнения позволяет найти ответ на следующие вопросы: Каков энергетический спектр микрочастицы дискретный E1,E2….En или непрерывный? Каков вид волновой функции В какой точке силового поля локализована микрочастица Волновая функция и ее свойства. Особенностью квантово-механического описания поведения микрочастиц является вероятностный подход. Причинно-следственная связь между событиями становится вероятностной. Вероятностной характеристикой поведения микрочастицы является величина, называемая амплитудой вероятности или «пси»-функцией. Эта волновая функция Правильную интерпретацию физического смысла волновой функции дал Борн.
Физический смысл имеет не сама волновая функция, а квадрат ее модуля.
Квадрат модуля волновой функции равен плотности вероятности нахождения частицы в соответствующем объеме пространства.
Так как вероятность нахождения частиц в заданном объеме V равна 1, то
Тогда Волновая функция должна быть: - непрерывной, так как описывает последовательное изменение поведения микрочастицы в некотором заданном пространстве; - однозначной и конечной, то есть давать один ответ на поставленный вопрос о месте нахождения микрочастицы; - интегрируемой и дифференцируемой по координатам и времени. Решение уравнения Шредингера существует не при любых, а только при некоторых значениях полной энергии, получивших название собственных значений, это следует из особого решения уравнения Шредингера, которое, с математической точки зрения, является однородным дифференциальным уравнением второго порядка с частными производствами. При этом возможные значения энергии образуют так называемый энергетический спектр микрочастиц.
Движение свободной частицы. Свободной является частица, движущаяся вдоль оси Х в свободном пространстве при отсутствии внешних силовых полей. В этих условиях потенциальная энергия частицы U=0. Уравнение Шредингера в одномерном случае движения: Обозначим
Так как < Получим, что все положительные частицы в пространстве (вдоль оси Х) равновероятны, с плотностью Определение значения полной энергии частицы:
Частица (свобод.) может иметь любую энергию (не квантуется).
|
|||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1881; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.219.166 (0.007 с.) |
 , которая является также функцией координат и времени.
, которая является также функцией координат и времени.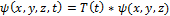

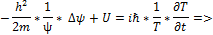
 - временное уравнение Шредингера.
- временное уравнение Шредингера. - оператор Лапласа
- оператор Лапласа




 или
или – Уравнение Шредингера для стационарных состояний.
– Уравнение Шредингера для стационарных состояний.

 описывает волновые свойства частиц.
описывает волновые свойства частиц.

 - условие нормировки.
- условие нормировки. – набор возможных значений энергии микрочастиц.
– набор возможных значений энергии микрочастиц. Как следует из особого решения подобных ДУ этим собственным значением энергии соответствуют волновые функции, которые называются собственными функциями
Как следует из особого решения подобных ДУ этим собственным значением энергии соответствуют волновые функции, которые называются собственными функциями  .
.
 . Решение уравнения Шредингера:
. Решение уравнения Шредингера:  – Эта функция представляет собой плоскую монохроматическую волну де Бройля.
– Эта функция представляет собой плоскую монохроматическую волну де Бройля.
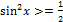 , то
, то