Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 31: Уравнение Шредингера.Содержание книги Поиск на нашем сайте
Э. Шредингер (1926) постулировал фундаментальное соотношение – основное уравнение нерелятивистской квантовой механики, справедливость которого (как и всяких постулатов) подтверждается согласием с опытом получаемых с его помощью результатов. Уравнение Шредингера – нерелятивистское уравнение относительно основной характеристики состояния микрообъектов – волновой функции ψ(r,t) – и имеет вид
где ħ = h/(2π), m – масса частицы, Δ – оператор Лапласа Подставив функцию (80) в уравнение Шредингера (79) и разделив левую и правую части на произведение ψ(r)·φ(t), получим
Так как левая часть уравнения (81) зависит только от r, а правая – только от t, то их можно приравнять одной и той же постоянной разделения, в качестве которой, как можно показать, можно выбрать Е – полную энергию частицы. Таким образом,
Уравнение (82) называют стационарным уравнением Шредингера. Его обычно записывают в более удобном виде:
Явный вид стационарного уравнения Шредингера определяется конкретной зависимостью U (r). Решая уравнение (83), получаем, что где С – произвольная постоянная. Подставляя (85) в (80), видим, что в случае стационарного силового поля состояние частицы описывается волновой функцией [постоянная С включена в функцию ψ(r) ], откуда следует, что стационарность состояния не исключает зависимости волновой функции от времени, а только ограничивает ее гармоническим законом
где ψ = ψ(x,y,z,t). С учетом того, что гамильтониан – уравнение Шредингера в операторной форме Подставив в стационарное уравнение Шредингера оператор полной энергии [см. (101)] получим стационарное уравнение Шредингера в операторной форме:
Вопрос 29: Принцип неопределенности Гейзенберга. Во многих случаях классические представления неприменимы для описания микрообъектов. В. Гейзенберг (1927) выдвинул идею о принципиальной невозможности измерения определенных пар связанных между собой характеристик частицы так, чтобы они одновременно имели точные значения. Согласно соотношению неопределенностей Гейзенберга, микрочастица (микрообъект) не может иметь одновременно точных значений координаты (х, у, z) и компонентов импульса (рх, py, pz), причем неопределенности этих величин удовлетворяют условию Δx·Δpx ≥ ħ, Δy·Δpy ≥ ħ, (74) Δz·Δpz ≥ ħ, т. е. произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка ħ. Следовательно, чем меньше неопределенность одной из величин (х, у, z или рх, ру, pz), тем больше неопределенность другой. В квантовой теории важна еще одна пара канонически сопряженных величин, для которой соотношение неопределенностей (соотношение неопределенностей для энергии и времени) имеет вид ΔEΔt ≥ ħ, (75) где ΔЕ – неопределенность энергии некоторого состояния системы, Δt – промежуток времени, в течение которого оно существует. Поэтому если в классической механике наличие координат и импульсов (скоростей) системы точно задает ее поведение во времени и пространстве, то предсказание поведения квантовой системы должно носить вероятностный характер.
Вопрос 28: Волны Де Бройля. Луи де Бройль в 1924 г. постулировал, что корпускулярно-волновой дуализм имеет универсальный характер и распространяется не только на световые корпускулы (фотоны), но и на все частицы материи: частицы вещества (в частности, электроны) наряду с корпускулярными обладают также и волновыми свойствами. Количественные соотношения, связывающие корпускулярные (энергия и импульс) и волновые [частота (длина волны)] характеристики микрочастиц, такие же, как для фотона: E = hv = ħω, p = h/λ = ħk, где k = 2π/λ – волновое число, а ħ = h/2π – постоянная Планка. Длина волны, связанная с частицей, где р – импульс частицы, λ называется длиной волны де Бройля. Для нерелятивистской частицы длина волны де Бройля Для релятивистской частицы длина волны де Бройля
(в данном случае Если Т – кинетическая энергия частицы, то Е = Т + т0с2. Тогда Гипотеза де-Бройля была блестяще подтверждена экспериментально. Дэвиссон и Джермер обнаружили, что пучок электронов, рассеивающийся от кристаллической пластинки, дает дифракционную картину. Томсон и независимо от него Тартаковский получили дифракционную картину при прохождении электронного пучка через металлическую фольгу. Экспериментальное доказательство наличия волновых свойств микрочастиц привело к выводу о том, что мы имеем дело с универсальным явлением – общим свойством материи Простейшей волной с частотой ω и волновым вектором k является плоская монохроматическая волна
где А – постоянная амплитуда волны, k – волновой вектор (его направление совпадает с направлением распространения волны, а модуль равен 2π/λ). Согласно корпускулярно-волновому дуализму материи, ω = E/ħ и р = ħk. Учитывая эти соотношения и выражение (72), видим, что с движением частицы, имеющей определенные энергию и импульс, связывается волна вида называемая плоской волной де Бройля.
Вопрос 27: Эффект Комптона. Эффект Комптона – упругое рассеяние коротковолнового электромагнитного излучения (рентгеновского и γ – излучений) на свободных (или слабосвязанных) электронах вещества, сопровождающееся увеличением длины волны. Разность Δλ = λ' - λ (комптоновскип сдвиг) не зависит от длины волны λ падающего излучения и от природы рассеивающего вещества, а зависит только от угла θ между направлениями рассеянного и первичного излучений: где λc = h/(moc) – комптоновская длина волны электрона [ т0 – масса покоя электрона, λc = 2,42631058·10-12 м].
закон сохранения импульса p = p' + p или, используя теорему косинусов, закон сохранения энергии W0 + E = W + E', (70) где p = hv/c, p' = hv'/c, Wo = moc2 – энергия электрона до столкновения (m0 – масса покоя электрона), E = hv – энергия налетающего фотона,
Вопрос 26: Фотоэффект. Фотоэффект – явление, подтверждающее гипотезу фотонов. Различают фотоэффект внешний, внутренний и вентильный. Внешним фотоэффектом (фотоэффектом) называют испускание электронов веществом (металлом, полупроводником, диэлектриком) под действием электромагнитного излучения. Внутренний фотоэффект – это вызванные электромагнитным излучением переходы электронов внутри полупроводника или диэлектрика из связанных состояний в свободные без вылета наружу. Разновидностью внутреннего фотоэффекта является вентильный фотоэффект – возникновение э.д.с. (фото-э.д.с.) при освещении контакта двух разных полупроводников или полупроводника и металла (при отсутствии внешнего электрического поля). Вентильный фотоэффект открывает пути для прямого преобразования солнечной энергии в электрическую. Фотоэффект обнаружен Герцем. Первые фундаментальные исследования фотоэффекта выполнены русским ученым А. Г. Столетовым. Измерив задерживающее напряжение, можно определить максимальные значения скорости и кинетической энергии фотоэлектронов. Внешний фотоэффект подчиняется следующим трем законам, полученным из обобщения опытных данных: I. Закон Столетова: при фиксированной частоте падающего света число фотоэлектронов, вырываемых из катода за единицу времени, пропорционально интенсивности света. II. Максимальная начальная скорость (максимальная начальная кинетическая энергия) фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой ν. III. Для каждого вещества существует «красная граница» фотоэффекта, т. е. минимальная частота v0 света (зависит от химической природы вещества и состояния его поверхности), ниже которой фотоэффект невозможен. Объяснение фотоэффекта дано на основе квантовой теории. Фотоэффект описывается уравнением Эйнштейна, выражающим закон сохранения энергии при фотоэффекте: т. е. энергия падающего фотона расходуется на совершение электроном работы выхода А из металла и на сообщение вылетевшему фотоэлектрону максимальной кинетической энергии. Подставляя в уравнение Эйнштейна (67) выражение (66), приходим к объяснению второго закона фотоэффекта
«Красная граница» зависит лишь от работы выхода электрона, т. е. от химической природы вещества и состояния его поверхности. Объяснение безынерционности фотоэффекта на основе квантовых представлений тривиально: испускание фотоэлектронов происходит сразу, как только на фотокатод падает излучение с ν > ν0.
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 276; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.110.231 (0.007 с.) |

 , (79)
, (79)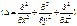 , i – мнимая единица, U (r,t) – потенциальная функция частицы в силовом поле, в котором частица движется. Это уравнение называют временным уравнением Шредингера. Если силовое поле, в котором частица движется, стационарно, т. е. функция U (r) не зависит от времени и имеет смысл потенциальной энергии, то решение уравнения (79) можно искать в виде произведения двух функций, одна из которых есть функция только координат, другая – только времени: ψ(r,t) = ψ(r)·φ(t) (80)
, i – мнимая единица, U (r,t) – потенциальная функция частицы в силовом поле, в котором частица движется. Это уравнение называют временным уравнением Шредингера. Если силовое поле, в котором частица движется, стационарно, т. е. функция U (r) не зависит от времени и имеет смысл потенциальной энергии, то решение уравнения (79) можно искать в виде произведения двух функций, одна из которых есть функция только координат, другая – только времени: ψ(r,t) = ψ(r)·φ(t) (80)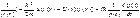 (81)
(81)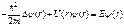 (82)
(82)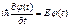 (83)
(83)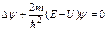 (84)
(84) , (85)
, (85)
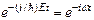 . В стационарном состоянии плотность вероятности
. В стационарном состоянии плотность вероятности 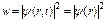 выражается только через ψ(r) и не зависит от времени. Общепринято ψ(r) также называть волновой функцией, хотя она является только координатной (амплитудной) частью волновой функции ψ(r,t) стационарного состояния. Временное уравнение Шредингера имеет вид [см. (79)]
выражается только через ψ(r) и не зависит от времени. Общепринято ψ(r) также называть волновой функцией, хотя она является только координатной (амплитудной) частью волновой функции ψ(r,t) стационарного состояния. Временное уравнение Шредингера имеет вид [см. (79)]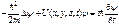 , (102)
, (102)
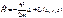 , уравнение (102) примет вид
, уравнение (102) примет вид 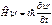 (103)
(103)
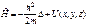 ,
,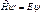 (104)
(104)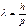 , (71)
, (71)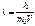 , где т0 – масса покоя частицы. Если Т – кинетическая энергия частицы [ Т=р2/(2т) ], то
, где т0 – масса покоя частицы. Если Т – кинетическая энергия частицы [ Т=р2/(2т) ], то  (71)
(71)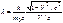
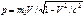 ). Выразив с помощью соотношения
). Выразив с помощью соотношения 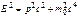 импульс частицы р через ее полную энергию Е, найдем
импульс частицы р через ее полную энергию Е, найдем 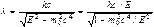
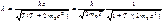 .
.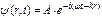 , (72)
, (72)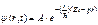 ,
,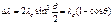 , (68)
, (68)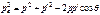 (69)
(69)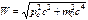 – энергия электрона после столкновения E ' = hv' – энергия рассеянного фотона.
– энергия электрона после столкновения E ' = hv' – энергия рассеянного фотона.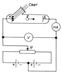 Два электрода (в вакуумной трубке подключены к батарее так, что с помощью потенциометра R можно изменять не только значение, но и знак подаваемого на них напряжения. Ток, возникающий при освещении катода монохроматическим светом, измеряется включенным в цепь миллиамперметром. Облучая катод светом различных длин волн, Столетов установил следующие закономерности, не утратившие своего значения до нашего времени: 1) наиболее эффективное действие оказывает ультрафиолетовое излучение; 2) под действием света вещество теряет только отрицательные заряды; 3) сила тока, возникающего под действием света, прямо пропорциональна его интенсивности. Чтобы фототок стал равным нулю, необходимо приложить задерживающее напряжение Uo. При U = Uo ни один из электронов, даже обладающий при вылете из катода максимальной скоростью Vmax, не может преодолеть задерживающего поля и достигнуть анода. Следовательно,
Два электрода (в вакуумной трубке подключены к батарее так, что с помощью потенциометра R можно изменять не только значение, но и знак подаваемого на них напряжения. Ток, возникающий при освещении катода монохроматическим светом, измеряется включенным в цепь миллиамперметром. Облучая катод светом различных длин волн, Столетов установил следующие закономерности, не утратившие своего значения до нашего времени: 1) наиболее эффективное действие оказывает ультрафиолетовое излучение; 2) под действием света вещество теряет только отрицательные заряды; 3) сила тока, возникающего под действием света, прямо пропорциональна его интенсивности. Чтобы фототок стал равным нулю, необходимо приложить задерживающее напряжение Uo. При U = Uo ни один из электронов, даже обладающий при вылете из катода максимальной скоростью Vmax, не может преодолеть задерживающего поля и достигнуть анода. Следовательно, 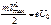 . (66)
. (66)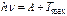 , (67)
, (67)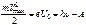 .
.