
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение плоской и сферической волн.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнение волны выражает зависимость смещения колеблющейся частицы от ее кординат Эта функция должна быть периодической относительно времени, т.к. она описывает колебания частицы с координатами на длину волны Найдём вид функции
Рис.8,2
Найдем уравнение колебания для точки с произвольным
величина Зафиксировав определенное значение фазы Таким образом, скорость распространения волны в уравнении (*) есть скорость перемещения фазы, поэтому ее называют фазовой скоростъю волны. Уравнение (*) описывает волны, распространяющиеся в сторону возрастания Уравнению волны можно придать более симметричный вид относительно
Теперь найдем уравнение сферической волны для точечного источника. Все точки сферической волновой поверхности волны в однородной и изотропной среде будут колебаться с одинаковой фазой. Если фаза источника Уравнение плоской волны, распространяющейся в произвольном направлении
Волновое уравнение
Уравнение волны является решением дифференциального уравнения, называемого волновым. Для его установления найдем вторые частные производные по времени и координатам от уравнения волны.
Аналогичные уравнения (3) и (4) можно записать для координат Сложив производные по координатам, получим:
Величина
Любая функция, удовлетворяющая уравнению (6), описывает некоторую волну, при этом корень квадратный из величины обратной коэффициенту при второй производной по времени дает фазовую скорость волны.
Энергия волны. Упругая среда, в которой распространяются механические волны, обладает как кинетической энергией колебательного движения частиц, так и потенциальной энергией, обусловленной деформацией среды при движении волны. Кинетическая энергия малого объема
Потенциальная энергия малого объема упруго – деформированной среды:
Сумма дает объемную плотность энергии упругих волн, т.е., объемную плотность механической энергии среды, обусловленную распространением волн, равную:
Если в среде распространяется продольная плоская волна вдоль оси
Подставим в уравнение (*)
Таким образом, объемная плотность энегрии волны зависит как от координаты, так и от времени. В каждый момент времени она разная в разных точках среды. В одной и той же точке она изменяется со временем по закону
т.е., пропорционально плотности среды, квадрату амплитуды и частоты.
Рис.8,3 а)
Рис.8,3б
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 605; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.164.100 (0.007 с.) |

 ,
,  ,
,  и времени
и времени  :
:  .
. , колеблются одинаковым образом.
, колеблются одинаковым образом. для плоской волны, для гармонических колебаний, распространяющихся вдоль оси
для плоской волны, для гармонических колебаний, распространяющихся вдоль оси  имеет вид:
имеет вид:

 . Значит колебания частиц в плоскости
. Значит колебания частиц в плоскости  от колебаний в плоскости
от колебаний в плоскости 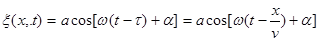
 * - уравнение плоской волны, распространяющейся в направлении оси
* - уравнение плоской волны, распространяющейся в направлении оси  ,
, - фаза волны, начальная фаза
- фаза волны, начальная фаза  определяется выбором начала отсчёта
определяется выбором начала отсчёта  .
. , можно найти связь между коорлинатой и временем для которых
, можно найти связь между коорлинатой и временем для которых  , а величина
, а величина  при этом даёт значение скорости, с которой перемещяется это значение фазы т.е., можно проследить движение определенной фазы волны. Взяв дифференциал от
при этом даёт значение скорости, с которой перемещяется это значение фазы т.е., можно проследить движение определенной фазы волны. Взяв дифференциал от  , получим:
, получим:  и
и  .
. .
. и волнового вектора
и волнового вектора  , где
, где  - нормаль к волновому фронту. Умножив числитель и знаменатель
- нормаль к волновому фронту. Умножив числитель и знаменатель  на
на  , получим:
, получим:  . Тогда,
. Тогда,  и уравнение волны:
и уравнение волны: .
. , то фаза точек волновой поверхности радиуса
, то фаза точек волновой поверхности радиуса  равна
равна  . Амплитуда колебаний сферической волны будет убывающей, даже если нет затухания и убывает по закону
. Амплитуда колебаний сферической волны будет убывающей, даже если нет затухания и убывает по закону  . Тогда уравнение сферической волны:
. Тогда уравнение сферической волны:  . Для поглощающей среды появится дополнительный множитель
. Для поглощающей среды появится дополнительный множитель  .
. имеет вид:
имеет вид:  .
. (1)
(1) (2), известно, что
(2), известно, что 
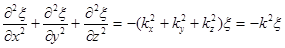 (5)
(5) обозначается знаком
обозначается знаком  и называется оператором Лапласа (лапласиан). Сопоставив уравнения (1) и (5), получим:
и называется оператором Лапласа (лапласиан). Сопоставив уравнения (1) и (5), получим: или
или 
 (6) – волновое уравнение.
(6) – волновое уравнение. среды с плотностью
среды с плотностью  , в котором все частицы движутся с одинаковой скоростью
, в котором все частицы движутся с одинаковой скоростью  равна:
равна: , а объемная плотность энергии
, а объемная плотность энергии  .
. , где
, где  - относительная деформация среды. Объемная плотность потенциальной энергии:
- относительная деформация среды. Объемная плотность потенциальной энергии:
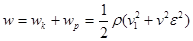 (*) для определенной координаты и времени.
(*) для определенной координаты и времени. , то скорость колебаний частиц малого объема:
, то скорость колебаний частиц малого объема: . А деформация этого объема:
. А деформация этого объема: .
. , получим:
, получим: - плоская волна.
- плоская волна. . Т.к., среднее значение
. Т.к., среднее значение 





