
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование формы поверхности второго порядка методом сечения плоскостямиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если дано каноническое уравнение поверхности S, то представление о поверхности можно получить по форме линий пересечения ее плоскостями: Z = h — параллельными координатной плоскости XO ' Y, X = h — параллельными координатной плоскости YO ' Z, Y = h — параллельными координатной плоскости XO ' Z. Уравнения проекций линий пересечения поверхности S c этими плоскостями на соответствующие координатные плоскости
Исследование поверхности второго порядка
Дано уравнение поверхности второго порядка: S: Приведение уравнения поверхности к каноническому виду Положим:
Уравнение (4.1) каноническое.
Исследование формы поверхности методом сечений плоскостями
Каноническое уравнение поверхности (4.1) задает однополостный гиперболоид. 1. Рассмотрим линии
Следовательно, Запишем полученное уравнение в виде:
Уравнение (4.3) определяет семейство эллипсов с центром в точках Полуоси эллипсов: При различных значениях h получим семейство соответствующих эллипсов:
Если h < 0, то уравнение (4.3)не меняет вида. Используя полученные данные, построим «карту» (см. рис.8).
Рис. 8. Сечения плоскостями, параллельными XO ' Y
Рассмотрим линии
Следовательно, уравнение проекций линий
Запишем уравнение (4.4) в виде:
Уравнение (4.5) определяет семейство гипербол в плоскостях Y = h (h — любое действительное число) с фокусами в точках При
При При
Уравнение (4.6) определяет семейство гипербол, которые повёрнуты на
Используя полученные данные, построим «карту» (см. рис.9).
Рис. 9. Сечения плоскостями, параллельными XO ' Z
Рассмотрим линии
Следовательно, уравнения проекций линий
Запишем уравнение (4.5) в виде:
Уравнения (4.8) — это уравнения гипербол в плоскостях При
При При
Уравнение (4.6) определяет семейство гипербол, которые повёрнуты на
Используя полученные данные, построим «карту» (см. рис.10).
Рис. 10. Сечения плоскостями, параллельными YO'Z
Проанализировав уравнение 1. уравнение 2. оси O'X, O'Y, O'Z являются осями симметрии поверхности, плоскости O'XZ, O'YZ, O ' XZ — плоскостями симметрии. Центром симметрии у поверхности является точка O(0,0,0); 3. рассекая поверхность горизонтальными плоскостями Z = h, в сечениях получаем эллипсы. 4. рассекая поверхность вертикальными плоскостями X = h и Y = h (h – любое действительное число), в сечениях получаем гиперболы. Поверхность однополостного гиперболоида бесконечна в направлении всех трех координатных осей. Построим её в канонической системе координат (см. рис. 11). Построение поверхности в канонической системе координат
Рис. 11. Поверхность в канонической системе координат Вывод
Таким образом, из вышеприведенного анализа следует, что, тип кривой второго порядка, заданной алгебраической формой, можно легко определить с помощью поворота осей и параллельного переноса начала координат. Так же из анализа следует, что зная знаки инвариантов, можно полностью определить тип линии второго порядка при различных значениях β, что мы и делаем. Четвёртая часть работы наглядно показывает, что исследование формы поверхности методом сечений плоскостями даёт хорошее представление о поверхности, которую мы исследуем. Данный способ исследования можно применять даже не зная, какая именно поверхность задана уравнением. Список используемой литературы 1. Бобылева Л. В., Брюхина Л. С. Линейная алгебра и аналитическая геометрия: Исследование кривых и поверхностей второго порядка: Учебно-методическое пособие — Дубна: Международный университет природы, общества и человека «Дубна», 2003. 2. Копылова Т. В. Аналитическая геометрия. — Дубна: Международный университет природы, общества и человека «Дубна», 1997
Размещено на Allbest.ru
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 2128; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.99.39 (0.006 с.) |

 получаются в результате подстановки в каноническое уравнение поверхности S Z = h, X = h, Y = h соответственно.
получаются в результате подстановки в каноническое уравнение поверхности S Z = h, X = h, Y = h соответственно.
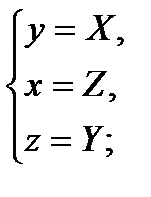
 .(4.1)
.(4.1) полученные в сечениях гиперболического параболоида плоскостями Z = h (h = const). Эти линии определяются системой уравнений:
полученные в сечениях гиперболического параболоида плоскостями Z = h (h = const). Эти линии определяются системой уравнений:
 (4.2)
(4.2) — уравнение проекций линий
— уравнение проекций линий  на плоскость XO ' Y.
на плоскость XO ' Y. (4.3)
(4.3) и вершинами в точках
и вершинами в точках  и
и  . Действительные оси эллипсов параллельны осям O'X и O ' Y.
. Действительные оси эллипсов параллельны осям O'X и O ' Y. и
и  увеличиваются с увеличением h.
увеличиваются с увеличением h.
 полученные в сечениях гиперболического параболоида плоскостями Y = h. Эти линии определяются системой уравнений:
полученные в сечениях гиперболического параболоида плоскостями Y = h. Эти линии определяются системой уравнений:
 на плоскость YO ' Z имеет вид:
на плоскость YO ' Z имеет вид: (4.4)
(4.4) (4.5)
(4.5) и
и  , полуосями
, полуосями  и
и 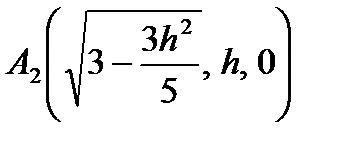 .
. получим семейство соответствующих гипербол:
получим семейство соответствующих гипербол:
 уравнение (4.4) определяет две пересекающиеся прямые.
уравнение (4.4) определяет две пересекающиеся прямые. запишем:
запишем: (4.6)
(4.6) относительно осей координат.
относительно осей координат.
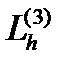 , полученные в сечениях однополостного гиперболоида плоскостями Z = h. Эти линии определяются системой уравнений:
, полученные в сечениях однополостного гиперболоида плоскостями Z = h. Эти линии определяются системой уравнений:
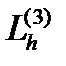 на плоскость YO ' Z имеют вид
на плоскость YO ' Z имеют вид (4.7)
(4.7) (4.8)
(4.8) (h — любое действительное число), с фокусами в точках
(h — любое действительное число), с фокусами в точках  и
и  , полуосями
, полуосями  и
и  .
. получим семейство соответствующих гипербол:
получим семейство соответствующих гипербол:
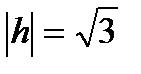 уравнение (4.7) определяет две пересекающиеся прямые.
уравнение (4.7) определяет две пересекающиеся прямые. запишем уравнение (4.7) в виде:
запишем уравнение (4.7) в виде:
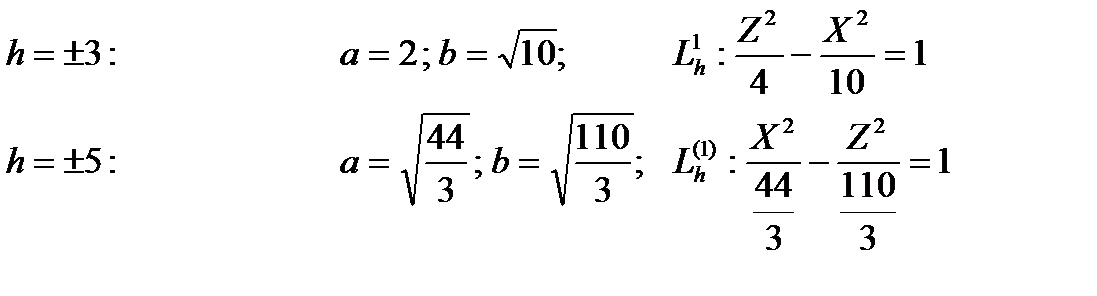
 задаёт однополостный гиперболоид.
задаёт однополостный гиперболоид.



