Развертки поверхностей геометрических тел

Разверткой поверхности геометрического тела называется плоская фигура, которая получается в результате совмещения всех граней или всех поверхностей, ограничивающих тело, с одной плоскостью. Поверхности некоторых геометрических тел криволинейной формы, например шара и других поверхностей вращения, нельзя развернуть в одну плоскость. Для развертки таких поверхностей используют способы приближенной развертки.

Развертка призмы

На рисунке 1, а изображена правильная прямая трехгранная призма. Боковая поверхность призмы состоит из трех равных прямоугольников, ширина и высота которых известны. Основания призмы проецируются на горизонтальную плоскость проекций в истинную величину.

Построим развертку боковой поверхности призмы (рисунок 1, б). Для этого вдоль горизонтальной прямой отложим три отрезка, равных стороне основания призмы . Из точек проведем вертикальные прямые, равные высоте призмы. Через полученные точки проведем горизонтальную прямую. Полученная фигура — прямоугольник, состоящий из трех прямоугольников, которые равны граням призмы, будет разверткой ее боковой поверхности. Совместим два основания призмы — равносторонние треугольники с разверткой боковой поверхности призмы.Пользуясь размером l, взятым с горизонтальной проекции призмы, и линией связи, построим на развертке точку Е, принадлежащую грани .

 

Рисунок 1 – Развертка поверхности призмы:

а) чертеж; б) полная развертка поверхности

 

 

Развертка пирамиды

 

Рисунок 2 – Развертка поверхности пирамиды:

а) чертеж; б) полная развертка поверхности

 

Развертка цилиндра

 

Рисунок 3 – Развертка поверхности цилиндра:

а) чертеж; б) полная развертка поверхности

 

Развертка конуса

 

 

Рисунок 4 – Развертка поверхности конуса:

а) чертеж; б) полная развертка поверхности

Самостоятельная работа 2.2

Выполнение кроссвордов - головоломок с применением аксонометрических проекций

Цели выполнения:

- развитие пространственного представления и логического мышления;

- отработка правил выполнения аксонометрических проекций.

Содержание:

В рабочей тетради студента решить кроссворд-головоломку, по аналогии придумать 2-3 слова и выполнить их в аксонометрических проекциях на листе формата А4 без выполнения рамки и основной надписи.

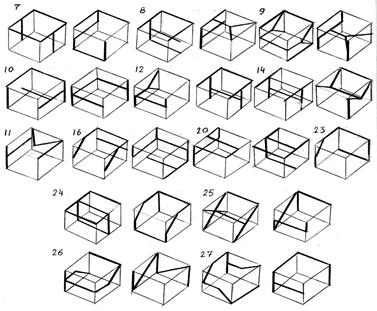
Рекомендации по выполнению:

Для решения подобных головоломок рассмотрим пример с фигурой, расположенной рядом со шрифтом на рисунке 5. Взглянув на кубик вдоль стрелки А, Вы увидите букву «Н». Направление Б откроет букву «П», а взгляд по стрелке В покажет букву «А». Сочетание этих букв дает слово «пан». В каждом задании – один или два кубика (см. рисунок 6), то есть три или шесть букв. Слова из них составляются по принципу анаграммы (например, из буквы КОС – образуют слово «сок»).

Рисунок 5

По вертикали:

По горизонтали:

Рисунок 6

Самостоятельная работа 2.3

Составление опорного конспекта на тему: «Сечение геометрических тел плоскостями» и выполнение упражнения

Цели выполнения:

- освоение метода прямоугольного проецирования плоскости геометрического тела;

- построение натурального вида фигуры сечения геометрического тела наклонной плоскостью на ортогональном чертеже и в аксонометрии.

Содержание:

На листе формата А3 начертить три проекции геометрического тела, построить натуральную фигуру сечения тела наклонной плоскостью и аксонометрическую проекцию заданного тела.

Рекомендуемая последовательность выполнения:

- по учебнику проработать раздел «Сечение геометрических тел плоскостями», изучить теоретическую часть работы, данную ниже;

- выполнить конспект темы (рекомендации по выполнению конспектов см. выше);

- составить алгоритм построения чертежа и компоновать чертеж, учитывая масштаб 1:1 или 1:2;

- начертить ортогональные проекции геометрического тела, линии построения можно не стирать;

- последовательно построить натуральную фигуру сечения тела наклонной плоскостью;

- выполнить аксонометрическую проекцию геометрического тела;

- проставить размеры шрифтом 3,5 и выполнить обводку чертежа.

При выполнении аксонометрической проекции обратите внимание на взаимосвязь ортогонального изображения и аксонометрии через аксонометрические оси, т.е. необходимо «привязать» изображение плоской фигуры к аксонометрическим осям Х,Y,Z.

При построении аксонометрической проекции усеченных геометрических тел, рекомендуется начинать построение с основания. Затем, от вершины каждого угла основания параллельно оси 0Y, откладывают соответствующие длины усеченных ребер, взятые с фронтальной или горизонтальной проекции. Построенные точки соединяют отрезками и получают фигуру среза.

 

Теоретическая часть