
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение развертки призмы.Содержание книги Поиск на нашем сайте
Наклонная призма (рис. 91) расположена так, что ее боковые ребра параллельны плоскости П2 и проецируются на нее в натуральную величину. Стороны оснований являются горизонталями и проецируются на плоскость П1 без искажения. Таким образом, длины сторон каждой грани известны, однако этого еще недостаточно для построения развертки. Боковые грани наклонной призмы являются параллелограммами, которые не могут быть построены по четырем сторонам. Для построения параллелограмма необходимо помимо длины сторон знать еще его высоту. Для определения высот граней пересечем призму плоскостью Σ перпендикулярной к ребрам, и определим натуральную величину сечения способом замены плоскостей проекций. Для построения развертки на свободном месте чертежа проводим горизонтальную прямую n и откладываем на ней отрезки 1 2 = 1424, 2 З = 2434 и 3 1 = 3414. Через точки 1, 2, 3, 1 проводим перпендикуляры к прямой n и откладываем на них величины боковых ребер так, чтобы А 1 = А 212 и 1 К = 12 К 2, В 2 = В 222 и 2 L = 22 L 2 и т. п.
Рассмотрим построение точки D, принадлежащей поверхности призмы. Также развертку можно построить методом раскатки.
Рис. 91 3 ПОСТРОЕНИЕ РАЗВЕРТОК КРИВЫХ РАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ
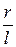 360o. 360o.
Построить развертку конуса.
Рис. 92
Развертка боковой поверхности прямого кругового цилиндра (рис. 93) представляет собой прямоугольник со сторонами, соответственно равными 2π r и l, где r –радиус окружности основания цилиндра, а l – его высота.
Рис. 93
Рассмотрим применение способа триангуляции к построению развертки эллиптического конуса (рис. 94). Триангуляция конической поверхности осуществляется вписыванием в нее пирамидальной поверхности, которая определяется ломаной 1 2 3 4..., вписанной в направляющую кривую конуса, и вершиной S. Развертка этой n -угольной пирамиды и принимается за развертку конуса. Все построения на рис. 94 выполняются аналогично построениям на рис. 90. Ломаная линия 1 2 3 4..., полученная на развертке пирамиды, заменяется плавной кривой, проходящей через те же точки.
Рис. 94
Рассмотрим построение развертки цилиндрической поверхности методом раскатки.
Рис. 95
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 952; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.206.19 (0.007 с.) |









