Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Две плоскости взаимно перпендикулярны, если одна из плоскостей содержит прямую перпендикулярную второй плоскости.Содержание книги
Поиск на нашем сайте
Рассмотрим два случая построения прямой перпендикулярной плоскости (на рис. 48, а – б плоскость задана следами, на рис. 48, в – треугольником). Исходя из выше рассмотренных построений (рис. 44), сначала необходимо в плоскости построить горизонталь и фронталь. Затем провести прямую l, перпендикулярную заданным плоскостям. На рис. 1, б l ^ P, l 1 ^ PП1, l 1 ^ h 1 и l 2 ^ PП2, l 2 ^ f 2. На рис. 48, в прямая l проведена перпендикулярно плоскости треугольника АВС через точку А (l ^ D АВС, l 1 ^ h 1 и l 2 ^ f 2). Условие перпендикулярности выполнено, и теперь необходимо задать плоскость любым из известных способов. На рис. 48 плоскость задана пересекающимися прямыми l ∩ m = К. Точка К на прямой l взята произвольно. Одна из прямых плоскости – перпендикуляр l, поэтому вторую прямую m можно провести под любым углом. Так как через току К можно провести множество прямых, то решение задачи может иметь множество вариантов (рис. 48, а).
Рис. 48
Двумя основными позиционными задачами, рассматриваемыми в этом разделе, являются: задача на пересечение прямой общего положения с плоскостью общего положения; задача на пересечение двух плоскостей общего положения. Прежде чем решать эти основные позиционные задачи рассмотрим частные случаи решения задач, когда геометрические образы занимают частное положение. Рассмотрим построение проекций точки К – точки пересечения прямой l общего положения с фронтально проецирующей плоскостью Р. На рис.49 плоскость задана следами (а), параллельными прямыми (б), треугольником (в). Фронтальная проекция фронтально проецирующей плоскости вырождается в прямую, а на рис. 49, а совпадет с фронтальным следом плоскости. Поэтому проекция К 2 точки пересечения должна лежать на этой прямой или на фронтальном следе плоскости. Точка принадлежит прямой l и плоскости Р. Поэтому проецируем точку К на горизонтальную проекцию l 1 прямой l. Дополним эпюры изображением видимых и невидимых участков прямой l, плоскость Р считаем непрозрачной. Часть прямой справа до точки К располагается выше плоскости Р, поэтому на П1 проекция этой части прямой видима до точки К1, другая часть прямой – невидима. Проекция прямой l на плоскости П2 будет полностью видимой, так как плоскость вырождается в прямую и не перекрывает проекцию l 2.
Рис. 49
Далее найдем точку пересечения прямой l с горизонтальной плоскостью P, заданной ее фронтальным следом РП2. В данном случае (рис. 50) плоскость Р параллельна П1 и, следовательно перпендикулярна к фронтальной плоскости проекций. Для плоскости Р в системе
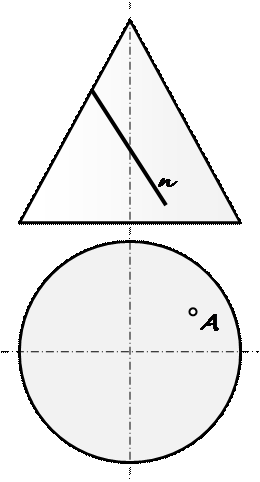
На рис.51 представлены случаи построения точки пересечения фронтально проецирующей прямой с плоскостью общего положения, заданной следами (рис. 51, а), треугольником (рис. 51, б), прямой и точкой вне прямой (рис. 51, в). Так как прямая l на П2 проецируется в точку, то проекция прямой совпадет с проекцией точки пересечения (К 2 º l 2). На первых двух эпюрах горизонтальная проекция К 1 найдена через горизонталь h, а на третьем через прямую общего положения n.
Рис. 51 Мы рассмотрели некоторые частные случаи пересечения прямой с плоскостью. Во всех этих случаях на эпюре одна из проекций точки пресечения была определена. Теперь рассмотрим частные случаи построения линии пересечения двух плоскостей. Построение линии пересечения двух плоскостей сводится к нахождению двух точек, общих для обеих заданных плоскостей, или одной такой точки при известном направлении искомой линии. На рис.52 и 53 для построения линии пересечения плоскостей можно использовать точку N пересечения следов PП1 и ГП1 и точку N ' пересечения следов PП2 и ГП2. Прямая NN ', проходящая через эти точки, является искомой линией пересечения. На рис.53 проекция линии пересечения NN ' совпадает со следом PП1, так как плоскость Р является горизонтально проецирующей. В случае на рис. 54 фронтальные следы плоскостей параллельны. Это значит, что искомая прямая параллельна плоскости П2 и для плоскостей P и Г является фронталью. Чтобы провести эту фронталь, достаточно построить одну принадлежащую ей точку. Используем точку К пересечения следов PП1 и ГП1. Построив проекции К 1 и К2, проводим l 1 параллельно оси х, а l 2 – параллельно следам PП2 и ГП2.
Рис. 52 Рис. 53 Рис. 54
На рис. 55 представлены случаи построения линии пересечения горизонтальной плоскости с плоскостью общего положения, заданной треугольником (рис. 55, а) и следами (рис. 55, б). Так как Р || П1, то линия пересечения является горизонталью. Чтобы построить эту горизонталь, достаточно построить две точки N и N ', общие для обеих заданных плоскостей (рис. 55, а), или одну точку при известном направлении искомой линии (рис. 55, б). На эпюре (рис. 56) одна из плоскостей фронтально проецирующая, а другая общего положения, заданная треугольником. Фронтальная проекция N 2 N '2 линиипересечения NN ' совпадет со следом ГП2, так как Г ^ П2.
Рис. 55 Рис. 56
Далее рассмотрим общие случаи решения основных позиционных задач, когда геометрические образы занимают общее положение.
1. Через данную прямую l провести вспомогательную плоскость частного положения Г (l Î Г); 2. Построить линию NN ' пересечения данной плоскости P и вспомогательной Г (Р ∩ Г = NN '); 3. Определить положение точки К пересечения прямых – данной l и построенной NN ' (l ∩ NN ' = К); 4. Определить видимость прямой l, используя конкурирующие точки. Далее представлены случаи решения задачи на пересечение прямой общего положения с плоскостью общего положения: плоскость задана треугольником (рис. 58); плоскость задана следами (рис. 59). Применяя выше приведенный алгоритм построения точки пересечения прямой с плоскостью, проводим через прямую l фронтально-проецирующую плоскость Г и строим линию NN ' пересечения обеих плоскостей – заданной и проведенной через l (рис. 58, а). Искомая точка К пересечения прямой l с плоскостью треугольника АВС находится в точке пересечения NN 'с l. Для определения участков прямой l, которые будут закрыты треугольником, следует воспользоваться анализом положения точек на скрещивающихся прямых (рис. 58, б). Например, точки 1 и N ' находятся на скрещивающихся прямых l и ВС. Фронтальные проекции этих точек совпадают (точки 1 и N ' – фронтально конкурирующие точки), т.е. точки 1 и N' одинаково удалены от П1. Но расстояния их от П2 различны, т.е. точка 1 находится дальше от П2, чем точка N '. Поэтому по отношению к П2 точка 1 закрывает точку N '. Следовательно, прямая l проходит перед треугольником АВС до точки К. Начиная от точки К влево прямая l закрывается треугольником, и поэтому этот участок показан штриховой линией.
Для выявления невидимого участка на горизонтальной проекции прямой l рассмотрим точки 2 и 3, лежащие соответственно на прямых l и АВ. Эти точки являются горизонтально конкурирующими – их проекции совпадают на П1. Если смотреть на эти точки сверху, то сначала видна точка 2. Следовательно, прямая l в этом месте закрыта треугольником АВС, и участок ее проекции от точки К до точки 3 должен быть показан штриховой линией. В данном случае точка К оказалась внутри контура треугольника АВС. При другом взаимном положении пересекающихся геометрических образов возможен случай, когда точка К окажется вне треугольника. Это означает, что прямая l пересекает плоскость, заданную треугольником АВС, вне контура этого треугольника. На рис. 59 для нахождения точки пересечения прямой с плоскостью через прямую l проводят горизонтально проецирующую плоскость Г (след ГП1 совпадает с l 1) и строят линию пересечения плоскостей Г и P, используя точки N и N 'пересечения их одноимённых следов. Искомая точка К находится в точке пересечения NN ' с l (l 2 ∩ N 2 N 2' = К 2). Видимость прямой определяют на основании анализа положения точек (используя конкурирующие точки). Например, взяв горизонтально конкурирующие точки 1 (1 Î l) и N (N Î PП1), видно, что точка 1 располагается выше относительно П1, чем точка N. Следовательно прямая l слева до точки К видима. За точкой К прямая показана штриховой линией – она невидима. Аналогично определяется видимость на фронтальной проекции.
Далее рассмотрим построение линии пересечения двух плоскостей общего положения. Как известно, построение линии пересечения двух плоскостей сводится к нахождению двух точек – общих для обеих заданных плоскостей. В данном случае обе точки можно найти, выполнив следующие построения (рис. 60): 1. Ввести две вспомогательные плоскости (посредники) частного положения Р и Р'; 2. Построить линии a, а ' и b, b ' пересечения данных плоскостей (Г и D) и вспомогательных Р и Р': Р ∩ Г = а, Р ∩ D = b; Р' ∩ Г = а ', Р' ∩ D = b '; 3. Определить положение точек N и N ' пересечения прямых a и b и прямых a 'и b ' соответственно: a ∩ b = N; a '∩ b '= N '; 4. Соединить точки N и N ', которые являются общими для обеих заданных плоскостей Г и D. NN ' – искомая линия пересечения плоскостей; 5. Определить видимость плоскостей Г и D. На рис. 61 найдена линия пересечения плоскостей, одна из которых задана параллельными прямыми а и b, а другая пересекающимися c и d. Для определения общих точек данных плоскостей введены две вспомогательные горизонтальные плоскости уровня Р и Р' и построены линии пересечения этих плоскостей с заданными Г (a || b) и D (с ∩ d). Через точки N и N ' пересечения этих линий проходит искомая прямая. Прямые 1-2 и 3-4, пересекаясь, дают точку N (N 1, N 2), а прямые 5-6 и 7-8 – точку N ' (N '1, N '2). Прямая NN ' (N 1 N 1', N 2 N 2') – искомая линия пересечения плоскостей.
Рис. 60 Рис. 61
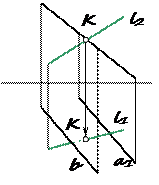
Если не применять профильную плоскость проекций, то можно ввести вспомогательную плоскость Σ ^ П1 (рис. 63, б) и построить линии пересечения ее с плоскостями P (1- 2) и Г (3- 4). Эти линии, пересекаясь дают искомую точку N (N 1, N 2), общую для плоскостей P и Г. Через N 1 и N 2 проводим проекции прямой n 1 и n 2 параллельно оси х.
Рис. 63 В качестве вспомогательных плоскостей для построения линий пересечения двух плоскостей можно использовать плоскости частного положения, которые проводят через прямые, принадлежащие плоскости (рис. 64).
Для определения видимости плоскостей при взаимном их пересечении взяты горизонтально проецирующие точки 5 и 6. Точка 5 принадлежит прямой АВ, а 6 – прямой DF. Анализ положения этих точек показывает, что на П1 точка 5 закрывает точку 6, а это значит, что прямая АВ в этом месте проходит над DF, т.е. треугольник АВС виден до прямой NN '. Аналогично определяется видимость на фронтальной проекции. Лекция № 5
СПОСОБЫ ПРЕОБРАЗОВАНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА 1. Общие сведения. 2. Способ замены плоскостей проекций. 3. Способ вращения. 1 ОБЩИЕ СВЕДЕНИЯ
Таким образом, при решении задачи бывает целесообразно преобразовать чертеж так, чтобы заданные геометрические образы занимали частное положение относительно плоскостей проекций. Для этого существуют различные способы преобразования комплексного чертежа. Каждый из них основан на одном из следующих принципов:
2 СПОСОБ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Сущность способа состоит в том, что одну из заданных плоскостей проекций (П1 или П2) заменяют новой плоскостью П4. При этом положение второй плоскости проекций и заданных геометрических образов остается неизменным. Новая плоскость проекций П4 выбирается таким образом, чтобы она занимала частное положение по отношению к геометрическому объекту и была при этом перпендикулярной к незаменяемой плоскости проекций. Исходная (старая) система плоскостей проекций Такое последовательное преобразование исходной системы плоскостей проекций позволяет получить новую систему, в которой рассматриваемые геометрические объекты займут частное положение относительно плоскостей проекций. Одновременно можно заменять только одну плоскость проекций П1 (или П2), другая плоскость П2 (или П1) должна оставаться неизменной.
В новой системе
3 СПОСОБ ВРАЩЕНИЯ
Проведем ось вращения i перпендикулярно П1 через точку В прямой АВ и начнем вращать точку А вокруг оси i
Решение четырех основных задач методом замены плоскостей проекций Все метрические и позиционные задачи, решаемые методом замены плоскостей проекций, можно свести к одной из нижеприведенных: 1. 2. Преобразовать прямую общего положения в проецирующую прямую (рис. 68).
3. Преобразовать плоскость общего положения в проецирующую (рис. 69, а), (определение углов наклона). 4. Преобразовать плоскость общего положения в плоскость уровня (рис. 69, б)(определение натуральной величины плоской фигуры).
Рис. 69
Лекция № 6 ПОВЕРХНОСТЬ 1. Основные понятия и термины. 2. Классификация поверхностей. 3. Построение точек и линий на поверхности. 4. Сечение поверхностей вращения проецирующими плоскостями. 1 ОСНОВНЫЕ ПОНЯТИЯ И ТЕРМИНЫ Поверхность – это множество всех последовательных положений движущейся линии.
Направляющая (n) – прямая или кривая линия, по которой скользит образующая (рис. 70). Ось (i) – прямая, вокруг которой перемещается образующая. Рис. 70 Очерк поверхности – совокупность точек ограничивающих ее на чертеже (контур поверхности). Существует несколько способов задания поверхностей: 1. Аналитический (поверхность задается уравнением); 2. Кинематический (поверхность рассматривается как траектория движения некоторых линий); 3. Каркасный (поверхность задается некоторым числом линий и точек, принадлежащих поверхности). Для задания поверхности часто используют определитель поверхности – совокупность условий, необходимых и достаточных для однозначного задания поверхности. Определитель содержит в себе геометрическую и алгоритмическую части – Ф (Г) [A]. Геометрическая часть содержит набор геометрических образов, участвующих в образовании поверхности. Алгоритмическая часть содержит перечень операций, совершаемых между геометрическими образами.
где Ф – поверхность, l – образующая, i – ось вращения.
2 КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ В зависимости от формы образующей поверхности делятся на линейчатые (образующая – прямая линия) и нелинейчатые (образующая – кривая линия). По закону движения образующих: с вращательным движением – поверхности вращения, с винтовым движением – винтовые поверхности, поверхности с плоскостью параллелилизма – множество образующих, параллельных некоторой плоскости и пересекающих две направляющие (цилиндроид, коноид, гиперболический параболоид), циклические поверхности – движение окружности постоянного или переменного радиуса. По признаку развертывания поверхности могут быть развертываемыми, которые можно развернуть на плоскости без разрывов и складок и неразвертываемыми. По признаку направляющих, которые могут быть ломаными, прямыми или кривыми, поверхности могут быть гранными или кривыми. Часть пространства, ограниченная со всех сторон поверхностью, называется телом. Рассмотрим две группы тел: многогранники и тела вращения. Многогранник – тело, ограниченное плоскими многоугольниками (гранями), которые пересекаются по прямым (ребрам).
Из числа многогранников выделяют группу правильных многогранников. Одно из древнейших упоминаний о правильных многогранниках находится в трактате Платона (427-347 до н. э.) "Тимаус". Поэтому правильные многогранники также называются платоновыми телами (хотя известны они были задолго до Платона). Каждый из правильных многогранников, а всего их пять, Платон ассоциировал с четырьмя "земными" элементами: огонь – тетраэдр (4 грани, рис. 73), земля – гексаэдр (6 граней, рис. 74) – куб, воздух – октаэдр (8 граней, рис. 75), вода – икосаэдр (20 граней, рис. 77), а также с "неземным" элементом – небом – додекаэдр (12 граней, рис. 76). Все грани правильного многогранника – равные между собой правильные многоугольники и в каждой его вершине сходится одно и то же число граней, а многогранные углы при вершинах – выпуклые. У таких многогранников число граней (Г), вершин (В) и ребер (Р) находится в определенной зависимости: Г + В – Р = 2 (формула Эйлера).
Особенностью таких поверхностей является то, что можно вписать сферу в любой правильный многогранник и описать сферу около любого правильного многогранника. Рис. 73 Рис. 74 Рис. 75 Рис. 76 Рис. 77
Кроме правильных выпуклых многогранников существуют и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Рассматривая пересечения продолжения граней Платоновых тел, мы будем получать звездчатые многогранники.
Поверхность вращения Поверхность вращения создается при вращении прямолинейной или криволинейной образующей вокруг неподвижной оси (рис. 78). Любая точка образующей описывает в пространстве окружность, плоскость которой перпендикулярна оси вращения. Эта окружность называется – параллелью. Самая большая параллель называется экватором, самая маленькая – горлом. Плоскость, которая проходит через ось вращения, рассекает поверхность вращения по меридиану. Если эта плоскость параллельна плоскости проекций, то меридиан проецируется без искажения и называется главным.
Поверхности вращения
Рис. 83 Рис. 84 Рис. 85 Рис. 86
Происхождение названий геометрических фигур
Почти все названия геометрических фигур греческого происхождения, как и само слово геометрия, происходящее от греческого слова γεωμετρία (геометриа) – землемерие. Но эти слова вошли в русский язык через латинский язык. Призма – латинская форма греческого слова πρισμα(присма) – опиленная (имелось в виду опиленное бревно). Пирамида – латинская форма греческого слова πυράμις (пюрамис), которым греки называли египетские пирамиды. Это слово происходит от древнеегипетского «пурама» – так пирамиды называли сами египтяне. Цилиндр – происходит от латинского слова cylindrus (цилиндрус), являющегося латинской формой греческого слова κύλινδρος (кюлиндрос), означающего валик, каток. Конус – латинская форма греческого слова κώνος (конос), означающего сосновая шишка. Сфера – латинская форма греческого слова σφαίρα (сфайра) – мяч. Трапеция – происходит от латинского слова trapezium (трапезиум) – латинской формы греческого слова τράπεςιον (трапезион) – столик. От этого же корня происходит наше слово «трапеза», означающее по-гречески стол. Ромб – происходит от латинского слова rombus (ромбус) – латинской формы греческого слова ρόμβος (ромбос), означающего бубен. Мы привыкли к тому, что бубен имеет круглую форму, но раньше они имели форму квадрата или ромба, о чем свидетельствуют изображения «бубен» на игральных картах. Именно с латинского языка мы заимствовали слово пункт, употребляющийся иногда в значении «точка» (отсюда «пунктир»), и слово линия. Пункт – происходит от латинского слова punctum (пунктум) – укол. Линия – происходит от латинского слова linea (линеа) – льняная (имеется в виду льняная нить). От этого же корня происходит наше слово «линолеум», первоначально означавшее промасленное льняное полотно.
3 ПОСТРОЕНИЕ ТОЧЕК И ЛИНИЙ НА ПОВЕРХНОСТИ
Точка принадлежит поверхности, если она находится на линии этой поверхности. План решения задачи на принадлежность точки поверхности включает: - определение вида заданной поверхности; - выбор графически простой для построения на чертеже линии поверхности, проходящей через заданную точку (прямая или окружность); - построение проекций этой линии на чертеже; - построение искомых проекций точки. Для лучшего представления и понимания эпюр каждой поверхности сопровождается наглядным изображением, а стрелкой указывается направление взгляда (фронтальная проекция – вид спереди).
Точки и линии на поверхности призмы
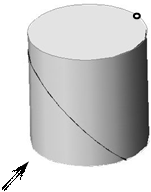
Рассмотрим построение точки и линии на поверхности прямой призмы.
Построить профильную проекцию цилиндра и недостающие проекции точки и прямой.
Построить профильную проекцию конуса и недостающие проекции точки и прямой.
Точки и линии на поверхности сферы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.6.140 (0.011 с.) |

 Если прямая l перпендикулярна плоскости P, то любая плоскость, проведенная через эту прямую, будет также перпендикулярна плоскости P. Поэтому через прямую l можно провести бесконечное множество плоскостей, что приводит к вариативности решения задач (рис. 47).
Если прямая l перпендикулярна плоскости P, то любая плоскость, проведенная через эту прямую, будет также перпендикулярна плоскости P. Поэтому через прямую l можно провести бесконечное множество плоскостей, что приводит к вариативности решения задач (рис. 47). а) б) в)
а) б) в)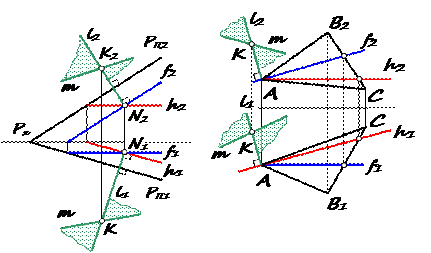


 дан только фронтальный след РП2 параллельный оси проекций х. Очевидно, что фронтальная проекция искомой точки пересечения должна лежать как на следе РП2, так и на фронтальной проекции прямой l (К 2 Î l 2, К 2 Î РП2 Þ К 2 = l 2 ∩ РП2). По проекции К 2 находим К 1 на l 1.
дан только фронтальный след РП2 параллельный оси проекций х. Очевидно, что фронтальная проекция искомой точки пересечения должна лежать как на следе РП2, так и на фронтальной проекции прямой l (К 2 Î l 2, К 2 Î РП2 Þ К 2 = l 2 ∩ РП2). По проекции К 2 находим К 1 на l 1. Так как правая часть прямой до точки К находится под плоскостью Р, то на чертеже соответствующая часть горизонтальной проекции изображена штриховой линией.
Так как правая часть прямой до точки К находится под плоскостью Р, то на чертеже соответствующая часть горизонтальной проекции изображена штриховой линией.

 а) б) в)
а) б) в)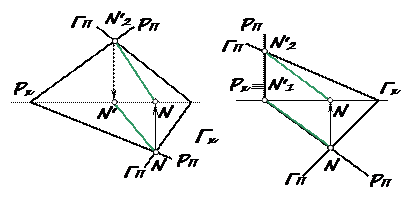



 а) б)
а) б) В общем случае для построения точки К пересечения прямой l с плоскостью P необходимо выполнить следующие построения (рис. 57):
В общем случае для построения точки К пересечения прямой l с плоскостью P необходимо выполнить следующие построения (рис. 57):

 Рассмотрим построение линии пересечения плоскостей P и Г, с использованием профильной плоскости проекций и без нее. Заданные плоскости являются профильно-проецирующими, а значит линия их пересечения n параллельна оси х и тоже является профильно-проецирующей прямой (рис. 62). Чтобы найти эту прямую, надо построить одну принадлежащую ей точку. В качестве вспомогательной плоскости можно использовать профильную плоскость проекций (рис. 63, а). Линия n проходит через точку N пересечения следов PП3 и ГП3.
Рассмотрим построение линии пересечения плоскостей P и Г, с использованием профильной плоскости проекций и без нее. Заданные плоскости являются профильно-проецирующими, а значит линия их пересечения n параллельна оси х и тоже является профильно-проецирующей прямой (рис. 62). Чтобы найти эту прямую, надо построить одну принадлежащую ей точку. В качестве вспомогательной плоскости можно использовать профильную плоскость проекций (рис. 63, а). Линия n проходит через точку N пересечения следов PП3 и ГП3.
 а) б)
а) б) На рис. 64 обе точки для обеих плоскостей найдены как точки пересечения (N и N ') сторон треугольника АВ и ВС с плоскостью, заданной треугольником DEF. Через прямую АВ проводят фронтально проецирующую плоскость Р, задав её следом PП2. Она пересекает плоскость треугольника DEF по прямой 1-2 (1121, 12-22), которая пересекается со стороной АВ в точке N (N 1, N 2). Фронтально проецирующая плоскость Р', проведенная через прямую ВС, задана следом Р'П2. Эта плоскость пересекает плоскость треугольника DEF по линии 3-4 (3141,32-42), которая в пересечении со стороной ВС дает точку N ' (N '1, N '2). NN ' – искомая линия пересечения плоскостей.
На рис. 64 обе точки для обеих плоскостей найдены как точки пересечения (N и N ') сторон треугольника АВ и ВС с плоскостью, заданной треугольником DEF. Через прямую АВ проводят фронтально проецирующую плоскость Р, задав её следом PП2. Она пересекает плоскость треугольника DEF по прямой 1-2 (1121, 12-22), которая пересекается со стороной АВ в точке N (N 1, N 2). Фронтально проецирующая плоскость Р', проведенная через прямую ВС, задана следом Р'П2. Эта плоскость пересекает плоскость треугольника DEF по линии 3-4 (3141,32-42), которая в пересечении со стороной ВС дает точку N ' (N '1, N '2). NN ' – искомая линия пересечения плоскостей. Часто трудоемкий процесс решения задачи во многом зависит не от сложности ее условия, а от положения заданных геометрических образов относительно плоскостей проекций. Если заданные геометрические образы занимают частные положения, то решение задачи, как правило, упрощается. При таком положении геометрических образов относительно плоскостей проекций мы непосредственно по чертежу получаем ответ на поставленный в задаче вопрос. Например, по рис. 65, б можно сразу определить расстояние между параллельными прямыми, а по рис. 65, а, этого сделать нельзя.
Часто трудоемкий процесс решения задачи во многом зависит не от сложности ее условия, а от положения заданных геометрических образов относительно плоскостей проекций. Если заданные геометрические образы занимают частные положения, то решение задачи, как правило, упрощается. При таком положении геометрических образов относительно плоскостей проекций мы непосредственно по чертежу получаем ответ на поставленный в задаче вопрос. Например, по рис. 65, б можно сразу определить расстояние между параллельными прямыми, а по рис. 65, а, этого сделать нельзя. может быть преобразована в новую систему
может быть преобразована в новую систему  при замене плоскости П1 плоскостью П4 ^ П2 или в систему
при замене плоскости П1 плоскостью П4 ^ П2 или в систему  при замене плоскости П2 плоскостью П4 ^ П1. Каждая из этих полученных систем может быть преобразована в новую путем замены плоскости проекций. Согласно этому, система
при замене плоскости П2 плоскостью П4 ^ П1. Каждая из этих полученных систем может быть преобразована в новую путем замены плоскости проекций. Согласно этому, система 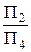 может быть преобразована в систему
может быть преобразована в систему  при замене плоскости П2 плоскостью П5 ^ П4, а система
при замене плоскости П2 плоскостью П5 ^ П4, а система  Рассмотрим замену фронтальной плоскости проекций П2, новой плоскостью П4, перпендикулярной к П1, и параллельной прямой АВ (рис. 66). В результате получим новую систему плоскостей проекций
Рассмотрим замену фронтальной плоскости проекций П2, новой плоскостью П4, перпендикулярной к П1, и параллельной прямой АВ (рис. 66). В результате получим новую систему плоскостей проекций  Рассмотрим вращение прямой АВ вокруг проецирующей прямой (рис. 67)
Рассмотрим вращение прямой АВ вокруг проецирующей прямой (рис. 67) П1. Плоскость, в которой располагается окружность, описываемая точкой, становится горизонтальной плоскостью уровня. Следовательно, окружность, описываемая точкой А в пространстве, спроецируется на плоскость П1 без искажения, а на плоскость П2 – в отрезок прямой параллельный оси х. При вращении прямой АВ вокруг оси i точка В останется неподвижной, так как она принадлежит оси вращения. Если необходимо найти натуральную величину прямой АВ, то прямую вращают до тех пор, пока она не займет положение параллельное плоскости П2.
П1. Плоскость, в которой располагается окружность, описываемая точкой, становится горизонтальной плоскостью уровня. Следовательно, окружность, описываемая точкой А в пространстве, спроецируется на плоскость П1 без искажения, а на плоскость П2 – в отрезок прямой параллельный оси х. При вращении прямой АВ вокруг оси i точка В останется неподвижной, так как она принадлежит оси вращения. Если необходимо найти натуральную величину прямой АВ, то прямую вращают до тех пор, пока она не займет положение параллельное плоскости П2. Преобразовать прямую общего положения в прямую уровня (рис. 68), (определение натуральной величины прямой и углов наклона).
Преобразовать прямую общего положения в прямую уровня (рис. 68), (определение натуральной величины прямой и углов наклона).
 а) б)
а) б)
 Образующая (l) – прямая или кривая линия, которая образует поверхность при своем движении (рис. 70).
Образующая (l) – прямая или кривая линия, которая образует поверхность при своем движении (рис. 70). Например, определитель цилиндрической поверхности вращения выглядит следующим образом: Ф (l, i) [ l çç i, l i ],
Например, определитель цилиндрической поверхности вращения выглядит следующим образом: Ф (l, i) [ l çç i, l i ], Многогранник, две грани которого равны и параллельны (конгруэнтны), а остальные пересекаются по параллельным прямым, называется призмой (рис. 71).
Многогранник, две грани которого равны и параллельны (конгруэнтны), а остальные пересекаются по параллельным прямым, называется призмой (рис. 71). Многогранник, одна грань которого – многоугольник (основание), а остальные грани треугольники с общей вершиной, называется пирамидой (рис. 72).
Многогранник, одна грань которого – многоугольник (основание), а остальные грани треугольники с общей вершиной, называется пирамидой (рис. 72).
 Звездчатый октаэдр является объединением двух пересекающихся правильных тетраэдров, и для его изготовления требуются лишь одинаковые равносторонние треугольники. Октаэдр имеет только одну звездчатую форму. Такой звездчатый многогранник в 1619 году описал Кеплер (1571-1630) и назвал его stella octangula – восьмиугольная звезда.
Звездчатый октаэдр является объединением двух пересекающихся правильных тетраэдров, и для его изготовления требуются лишь одинаковые равносторонние треугольники. Октаэдр имеет только одну звездчатую форму. Такой звездчатый многогранник в 1619 году описал Кеплер (1571-1630) и назвал его stella octangula – восьмиугольная звезда. Малый звездчатый додекаэдр – двенадцать правильных пятиугольных пирамид, основания которых совпадают с гранями додекаэдра.
Малый звездчатый додекаэдр – двенадцать правильных пятиугольных пирамид, основания которых совпадают с гранями додекаэдра. Большой икосаэдр – самый красивый и де-коративный из правильных звёздчатых многогранников Кеплера-Пуансо. Его вершины представляют собой центры правильных пятиугольных звёзд, выступающих из тела многогранника.
Большой икосаэдр – самый красивый и де-коративный из правильных звёздчатых многогранников Кеплера-Пуансо. Его вершины представляют собой центры правильных пятиугольных звёзд, выступающих из тела многогранника.
 1. Коническая поверхность вращения: Ф (l, i) [ l Ç i = S, l i ] (рис. 79).
1. Коническая поверхность вращения: Ф (l, i) [ l Ç i = S, l i ] (рис. 79). 2. Цилиндрическая поверхность вращения: Ф (l, i) [ l çç i, l i ] (рис. 80).
2. Цилиндрическая поверхность вращения: Ф (l, i) [ l çç i, l i ] (рис. 80). 3. Если вокруг прямой оси вращать окружность или ее дугу, распо-ложенную с ней в одной плоскости, то сформируется торовая поверхность – Ф (l, i) [ l i, О Ï i ] или как частный случай – сфера, которая образуется вращением окружности вокруг оси, проходящей через ее диаметр – Ф (l, i) [ l i, О Î i ], где l – образующая окружность, i – ось вращения, О – центр окружности (рис. 84).
3. Если вокруг прямой оси вращать окружность или ее дугу, распо-ложенную с ней в одной плоскости, то сформируется торовая поверхность – Ф (l, i) [ l i, О Ï i ] или как частный случай – сфера, которая образуется вращением окружности вокруг оси, проходящей через ее диаметр – Ф (l, i) [ l i, О Î i ], где l – образующая окружность, i – ось вращения, О – центр окружности (рис. 84).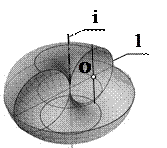



 Торы бывают: открытый тор – кольцо (рис. 81), закрытый (рис. 82), самопересекающийся (рис. 83, 85). Тор (рис. 61) называют также лимоновидным. В технике применяется еще одна торовая поверхность – глобоид (рис. 86), но ее следует рассматривать как внутренний отсек кольца.
Торы бывают: открытый тор – кольцо (рис. 81), закрытый (рис. 82), самопересекающийся (рис. 83, 85). Тор (рис. 61) называют также лимоновидным. В технике применяется еще одна торовая поверхность – глобоид (рис. 86), но ее следует рассматривать как внутренний отсек кольца.
 Рис. 79 Рис. 80 Рис. 81 Рис. 82
Рис. 79 Рис. 80 Рис. 81 Рис. 82