Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткий иллюстрированный курсСодержание книги Поиск на нашем сайте
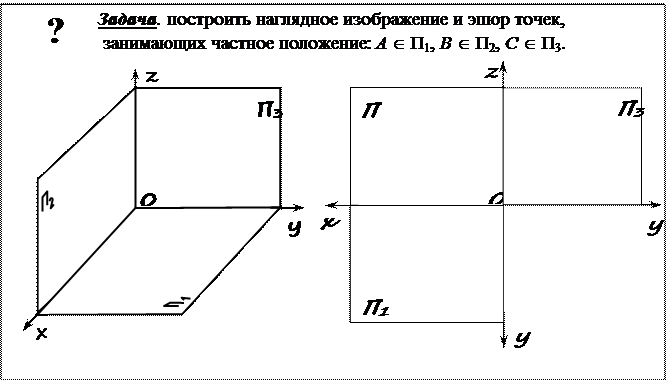
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ. КРАТКИЙ ИЛЛЮСТРИРОВАННЫЙ КУРС ДЛЯ РАБОТЫ НА ЛЕКЦИИ
В учебном пособии рассмотрены основные темы учебного курса начертательной геометрии: комплексные чертежи фигур; преобразования комплексного чертежа; позиционные и метрические задачи; развертки поверхностей; аксонометрические проекции. Предназначено для работы на лекции, так как содержание лекций незавершенное и требует дополнений
Печатается по решению редакционно-издательского совета Кузбасского государственного технического университета.
ПРЕДИСЛОВИЕ
Краткий иллюстрированный курс представлен в виде лекций, предназначенных для студентов машиностроительных специальностей. Их содержание соответствуют программе курса начертательной геометрии. Начертательная геометрия входит в состав учебной дисциплины федерального значения. Она является первой инженерной дисциплиной, которую изучает студент на первом курсе. Это единственная дисциплина, целью которой является непосредственно обучение студентов работе с различной по виду и содержанию графической информацией, основам графического представления информации, методам графического моделирования геометрических объектов, правилам разработки и оформления конструкторской документации, графических моделей, явлений и процессов. Графическая информация является средством общения во всех сферах деятельности человека. Поэтому в процессе изучения графических дисциплин студент должен приобрести навыки работы с любой по назначению и виду графической информацией, в том числе и с графическими документами, выполненными средствами компьютерной графики. Государственный образовательный стандарт устанавливает требования к содержанию и объему дисциплины в зависимости от специальности или направления. Содержание начертательной геометрии для специальностей машиностроительного профиля включает следующие темы: · Предмет начертательной геометрии; · Задание точки, прямой, плоскости и многогранников на комплексном чертеже Монжа; · Позиционные задачи; · Метрические задачи; · Способы преобразования чертежа; · Многогранники; · Поверхности; · Построение разверток поверхностей; · Аксонометрические проекции. Предложенный вариант чтения лекций отличается от традиционного (монологического). В нашем вузе такое чтение лекций проводится впервые. Лекции проходят по диалогическому типу в форме беседы. Каждая лекция имеет четкий план (перечень тем, которые будут рассмотрены на лекции). Кроме теории (основных положений), подлежащей усвоению и запоминанию, лекции содержат чертежи, причем чертежи на плоскости дополнены наглядными изображениями для лучшего понимания и усвоения материала. Цветовое решение способствует повышению интереса студентов к учебной информации. Для активизации познавательной деятельности студентов содержание лекций незавершенное, т.е. студенту на лекции необходимо завершить изображение или дополнить теоретическую часть. Чтобы легче было ориентироваться в лекции, напротив незавершенного изображения или текста стоит знак вопроса. В процессе беседы преподавателя со студентами выясняется, какие необходимы дополнения в лекции. Для лучшего усвоения материала после каждой темы студенту предлагается решить задачу. Учебное пособие, проработанное на лекции, студенты используют для решения задач в рабочей тетради по начертательной геометрии для самостоятельной работы. При таком изложении лекционного материала студент проходит три ступени усвоения знаний: понимание, запоминание и применение на практике. Использование учебного пособия позволяет повысить наглядность и подробность представления учебной информации. При этом студенты сосредоточивают внимание на изучаемом материале, что способствует интенсификации процесса обучения начертательной геометрии, повышая качество знаний и формируя умения и навыки, необходимые студентам в дальнейшем обучении.
ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
1. Плоскости проекций: горизонтальная – П1; фронтальная – П2; профильная – П3; дополнительная – П4, П5, … 2. Точки – А, В, С, D … или 1, 2, 3, 4, … 3. Проекции точек на плоскость: П1 – А 1, В 1, С 1, D 1, … или 11, 21, 31, 41, …; П2 – А 2, В 2, С 2, D 2, … или 12, 22, 32, 42, …; П3 – А 3, В 3, С 3, D 3, … или 13, 23, 33, 43, … 4. Точки на развертках – А 0, В 0, С 0, D 0, … или 10, 20, 30, 40, … 5. Линии – a, b, с, d … 6. Проекции на плоскость: П1 – а 1, b 1, с 1, d 1, …; П2 – а 2, b 2, с 2, d 2, …; П3 – а 3, b 3, с 3, d 3, … 7. Линии уровня: горизонталь – h; фронталь – f. 8. Прямая, проходящая через точки А и В – АВ. 9. Плоскости – Γ, Δ, Ρ, Σ, Τ, Ψ, Ω, … 10. Углы – α, β, γ, … 11. Координатные оси проекций: абсцисс – х или х 1,2; ординат – у; аппликат – z. 12. Новые оси абсцисс, полученные при замене плоскостей проекций – х 1,4, х 2,4, х 1,5, х 2,5 … 13. Символы, обозначающие отношения между геометрическими образами:
14. Греческий алфавит:
15. Латинский алфавит:
ВВЕДЕНИЕ
Согласно математическому энциклопедическому словарю: «Начертательная геометрия – раздел геометрии, в котором пространственные фигуры, а также методы решения и исследования пространственных задач изучаются с помощью их изображений на плоскости». Методы начертательной геометрии являются теоретической базой для решения задач технического черчения. Для того чтобы правильно выразить свои мысли с помощью рисунка, эскиза, чертежа требуется знание теоретических основ построения изображений геометрических объектов, их многообразие и отношения между ними, что и составляет предмет начертательной геометрии. Изображение фигуры на плоскости как графический способ представления информации о ней имеет преимущества в сравнении с другими способами: – общение становится более доступным, потому что образы, создаваемые на основе визуального (зрительного) восприятия, обладают большей, чем слова, ассоциативной силой; – изображения являются интернациональным языком общения, тогда как, например, вербальное общение требует для понимания, как минимум, знания языка собеседника. Задача этой науки – создание оптимальных геометрических форм объектов машиностроения, архитектуры и строительства, разработка теории графического отображения объектов и процессов. История развития начертательной геометрии, как способа изображения, уходит в далекое прошлое. В конце XVIII в. французский ученый и инженер Гаспар Монж (1746 – 1818 гг.) обобщил и научно обосновал накопившийся опыт создания проекционных изображений. Только в 1871 г. труды Монжа получили возможность публикации. В России курс начертательной геометрии впервые прочитан в 1810 г. в Петербургском институте корпуса инженеров путей сообщения. В XIX – ХХ в.в. большой вклад в разработку методов проецирования изображений внесли русские ученые Я. А. Севастьянов, Н. И. Макаров, В. И. Курдюмов, А. И. Добряков, Н. А. Рынин, Н. А. Попов, С. М. Колотов, Н. Ф. Четверухин, И. И. Котов и др. Начертательная геометрия завоевала свое достойное место в высшей школе как наука. Важнейшее прикладное значение начертательной геометрии как учебной дисциплины состоит в том, что она учит владеть графическим языком, выполнять и читать чертежи и другие изображения геометрических объектов, без чего немыслимо формирование инженера. Она обеспечивает преемственность между школьными курсами геометрии и черчения и графическими дисциплинами вуза. Изучение начертательной геометрии способствует развитию пространственного воображения и навыков правильного логического мышления. Совершенствуя способность – по плоскому изображению мысленно создавать представления о форме предмета и наоборот. В технике чертежи являются основным средством выражения человеческих идей. Они должны не только определять форму и размеры предметов, но и быть достаточно простыми и точными в графическом исполнении, помогать всесторонне исследовать предметы и их отдельные детали. Эти требования к чертежам и привели к созданию теории изображений, составляющей основу начертательной геометрии. Правила построения изображений основаны на методе проекций. Поэтому проекционный метод построения изображений является основным методом начертательной геометрии. Основные задачи курса: Изучение методов отображения пространственных объектов на плоскости (составление чертежа); Изучение способов определения при помощи чертежа формы и размеров предмета (чтение чертежа); Изучение способов графического и аналитического решения различных геометрических задач; Ознакомление с основными требованиями стандартов ЕСКД. Развитие навыков техники выполнения чертежей. Лекция № 1
ОБРАЗОВАНИЕ ПРОЕКЦИЙ 1. Геометрические образы. 2. Виды проецирования. 3. Ортогональное проецирование точки на две взаимно перпендикулярные плоскости. 4. Ортогональное проецирование точки на три взаимно перпендикулярные плоскости.
1 ГЕОМЕТРИЧЕСКИЕ ОБРАЗЫ
Изображаемые предметы (объекты) на чертежах принято называть геометрическими образами. Простейшим геометрическим образом является идеальная точка – объект, не имеющий измерений. Поэтому её считают нульмерной. Непрерывное и последовательное движение точки образует линию – одномерный геометрический образ, длину которого можно измерить. В свою очередь, линии бывают плоскими, если некоторая точка перемещается по плоскости, и пространственными, если некоторая точка перемещается в пространстве, меняя направление перемещения в трёхмерном пространстве. Непрерывное и последовательное движение линии образует плоскость – двумерный геометрический образ (можно измерить площадь данного рассматриваемого объекта) или поверхность – трехмерный геометрический образ. 2 ВИДЫ ПРОЕЦИРОВАНИЯ
В основу любого изображения положена операция проецирования. Различают два вида проецирования: Центральное – проецирующие лучи выходят из одной точки S (центра проецирования), удаленной на определенном (конечном) расстоянии от плоскости проекций (рис. 1). Если заданы центр проекций и плоскость проекций, то всегда можно получить проекцию точки на эту плоскость, но имея только проекцию точки, нельзя по ней определить положение точки в пространстве, так как любая точка проецирующего луча проецируется в ту же точку на плоскости.
П1 – плоскость проекций А, В – точки в пространстве О – начало координат А 1, В 1 – центральные проекции точек А и В на плоскости П1 X, Y – оси координат SA, SB – проецирующие лучи S и П1 – аппарат проецирования SA ∩ П1 = А 1; SB ∩ П1 = В 1 Рис. 1
Параллельное – частный случай центрального проецирования, когда центр проецирования удален в бесконечность, при этом проецирующие лучи можно рассматривать как параллельные проецирующие прямые. В свою очередь параллельные проекции подразделяются на прямоугольные (ортогональные), когда проецирующие прямые перпендикулярны плоскости проекций (рис. 2), и косоугольные, когда направление проецирования образует с плоскостью проекций угол не равный 90° (рис. 3).
Рис. 3 Рис. 2
На практике нашел применение метод __________________________ проецирования, вследствие его простоты построения и возможности получения неискаженных размеров. Применяется для построения чертежей изделий. По изображению на плоскости нельзя восстановить точку или фигуру и ее положение в пространстве, т.е. чертеж, содержащий одну проекцию точки или фигуры, необратим. Поэтому должны быть заданы дополнительные условия. Одним из методов, позволяющих добиться обратимости чертежа, является увеличение числа плоскостей проекций.
3 ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ ТОЧКИ НА ДВЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ
В соответствии с методом, предложенным Г. Монжем, рассмотрим в пространстве две взаимно перпендикулярные плоскости проекций (рис. 4). Одну из плоскостей проекций П1 располагают горизонтально и называют горизонтальной, а вторую П2 – вертикально и называют фронтальной. Плоскости бесконечны и непрозрачны. Плоскости проекций делят пространство на четыре двугранных угла – четверти (квадранты). Рассматривая ортогональные проекции, предполагают, что наблюдатель находится в первой четверти. Точку проецируют одновременно на 2 взаимно-перпендикулярные плоскости проекций. При построении проекции необходимо помнить, что ортогональной проекцией точки на плоскость называется основание перпендикуляра, опущенного из данной точки на эту плоскость. Проекции точки всегда расположены на прямых, перпендикулярных оси x и пересекающих эту ось в одной и той же точке Ах.
П1 – горизонтальная плоскость проекций; П2 – фронтальная плоскость проекций; П2 ^ П1 ; А – точка в пространстве; О – начало координат; А 1 – горизонтальная проекция точки А; А 2 – фронтальная проекция точки А; x, y – оси координат; АA 1 ∩ П1 = А 1 ; АА 2 ∩ П2 = А 2; I, II, III, IV – четверти; А 2 АX = ZA – расстояние от точки до плоскости П1(координата Z точки А); А 1 АX = уA – расстояние до плоскости П2 (координата у точки А); ОАX = хA – координата х точки А;
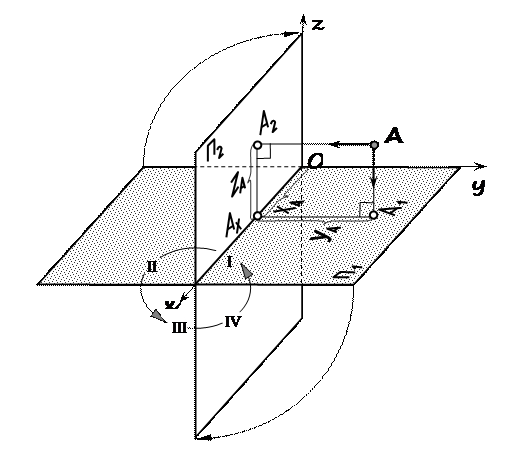
Рис. 4 Две проекции точки определяют положение точки в пространстве относительно заданной системы плоскостей. При решении задач пользоваться пространственным чертежом неудобно, поэтому от пространственного чертежа переходят к плоскому, который называют комплексным чертежом или эпюром (от франц. еpure – чертеж). Эпюр часто называют эпюром Монжа. Плоскость П2 остается неподвижной, а плоскость П1 вращается вокруг оси х на 90° до совмещения с плоскостью П2. По эпюру можно определить расстояние от точки до плоскости (рис. 5). ПрямаяА 1 А 2 называется вертикальной линией связи и располагается всегда перпендикулярно оси х.
4 ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ ТОЧКИ НА ТРИ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ
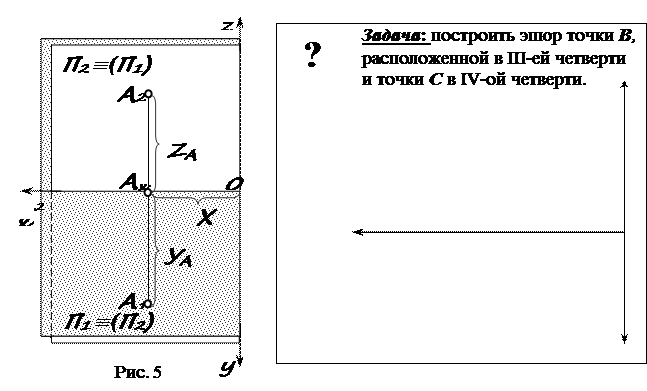
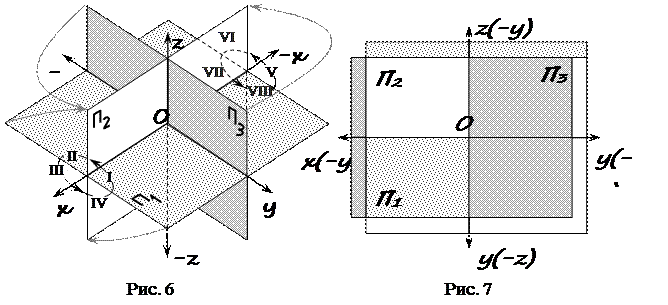
При решении задач бывает недостаточно двух проекций. Поэтому вводят третью плоскость перпендикулярно плоскостям П1 и П2. Ее называют профильной плоскостью (П3). Три плоскости делят пространство на 8 частей – октантов (рис. 6). Как и прежде, будем считать, что зритель, рассматривающий предмет, находится в первом октанте. Чтобы получить эпюр (рис. 7) любого геометрического образа плоскости П1 и П3 вращают, как показано на рис. 6. Плоскости проекций, попарно пересекаясь, определяют три оси x, y и z, которые можно рассматривать как систему декартовых координат в пространстве с началом в точке О.
Для получения эпюра точки в системе трех плоскостей проекций плоскости П1 и П3 вращают до совмещения с плоскостью П2 (рис. 8). При обозначении осей на эпюре отрицательные полуоси обычно не указывают. Для нахождения профильной проекции точки поступают следующим образом: из фронтальной проекции А 2 точки А проводят прямую перпендикулярно оси Z и на этой прямой от оси z откладывают отрезок, равный координате у точки А (рис. 9).
Рис.8 Рис. 9
Координатами называют числа, которые ставят в соответствие точке для определения ее положения в пространстве или на поверхности. В трехмерном пространстве положение точки устанавливают с помощью прямоугольных декартовых координат x, y и z (абсцисса, ордината и аппликата):
 абсциссах = ………..= …..…..= ….….. = ……….. – расстояние от точки до плоскости П3; абсциссах = ………..= …..…..= ….….. = ……….. – расстояние от точки до плоскости П3;
ординатау = ……….= ………= …...... = ………… – расстояние от точки до плоскости П2; аппликата z= …….. = ………= ……..= ………… – расстояние от точки до плоскости П1
А 1 А 2 – вертикальная линия связи, перпендикулярная оси х; А 2 А 3 – горизонтальная линия связи, перпендикулярная оси z.
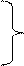 А 1 (….,….) Положение проекции каждой точки А 1 (….,….) Положение проекции каждой точки
А 2 (….,….) определяется двумя координатами А 3 (….,….)
Если точка принадлежит хотя бы одной плоскости проекций, она занимает частное положение относительно плоскостей проекций. Если точка не принадлежит ни одной из плоскостей проекций, она занимает общее положение.
Лекция № 2 ПРЯМАЯ 1. Прямая. 2. Положение прямой относительно плоскостей проекций. 3. Принадлежность точки прямой. 4. Следы прямой. 5. Деление отрезка прямой в данном соотношении. 6. Определение длины отрезка прямой и углов наклона прямой к плоскостям проекций. 7. Взаимное положение прямых.
Проекцией прямой в общем случае является прямая, за исключением случая, когда прямая перпендикулярна плоскости (рис. 10). Чтобы построить эпюр прямой определяют координаты x, y, z двух точек прямой и переносят эти величины на чертеж.
2 ПОЛОЖЕНИЕ ПРЯМОЙ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИИ
k1 < |k| k2 < |k| k3 < |k| Различают восходящую прямую – это прямая, которая по мере удаления от наблюдателя повышается (рис. 11) и нисходящую, которая понижается.
h ïê П1; Z = const
h 3 ïê 0 у горизонтали h 1 = | h | – свойство горизонтали a – угол наклона прямой к плоскости П1 b – угол наклона прямой к плоскости П2 g – угол наклона прямой к плоскости П3
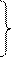 a = 0° a = 0°
b = (h 1 Ù П2) обозначить
f ïê П2; у = const
f 3 ïê 0 z фронтали f 2 =| f | – свойство фронтали
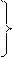 b = 0° b = 0°
a = (f 2 Ù П1) обозначить g = (f 2 Ù П3) на чертеже
р ïê П3; х = const
р 2 ïê 0 z профильной прямой
р 3 = | р | – свойство профильной прямой
b = (р 3 Ù П2) на чертеже
а ^ П1
а 3 ^ 0 у
b = g =
b ^ П2
b 3 ^ 0 z
b = g =
c ^ П3
с 2 ^ 0 z
b = g =
3 ПРИНАДЛЕЖНОСТЬ ТОЧКИ ПРЯМОЙ
М Î АВ, Е Ï АВ.
Справедлива обратная теорема: М 1 Î A 1 B 1; М 2Î A 2 B 2 Þ М Î АВ. Рис. 18 4 СЛЕДЫ ПРЯМОЙ
чертеже (рис. 19) F = k ∩ П 2 – фронтальный след
Правило построения следов: Для построения горизонтального следа прямой ….. необходимо фронтальную проекцию ….. прямой ….. продолжить до пересечения с осью Х, затем из точки пересечения с осью Х восстановить к ней перпендикуляр, и продолжить горизонтальную ….. проекцию прямой …… до пересечения с этим перпендикуляром. Фронтальный след строиться аналогично.
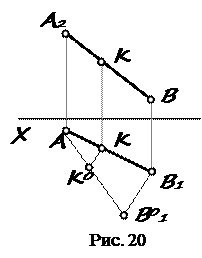
5 ДЕЛЕНИЕ ОТРЕЗКА ПРЯМОЙ В ДАННОМ СООТНОШЕНИИ Из свойств параллельного проецирования известно, что если точка делит отрезок прямой в данном отношении, то проекции этой точки делят одноименные проекции прямой в том же соотношении. Поэтому, чтобы некоторый отрезок разделить на эпюре в данном соотношении, надо в том же отношении разделить его проекции. Зная это условие можно определить принадлежность точки К прямой АВ: А 2 К 2: К 2 В 2 ¹ А 1 К 1 : К 1 В 1 Þ К Ï АВ Пример: Чтобы разделить отрезок АВ в отношении 2: 3 из точки А 1 проведем произвольный отрезок А 1 В 01 разделенный на пять равных частей (рис. 20): A 1 K 01 = 2 частям, K 01 B 01 = 3 частям, А 1 К 01 : К 01 В 01 =2: 3 Соединить точку В 01 с точкой В 1 и проведя из точки К 01 прямую параллельную (В 1 В 01) получим проекцию точки К 1. Согласно теореме Фалеса (Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие другую сторону, то на другой стороне отложатся равные между собой отрезки) А 1 К 1 : К 1 В 1 = = 2: 3, далее находим К 2. Таким образом проекции точки К делят одноименные проекции отрезка АВ в данном отношении следовательно и точка К делит отрезок АВ в отношении 2: 3.
6 ОПРЕДЕЛЕНИЕ ДЛИНЫ ОТРЕЗКА ПРЯМОЙ И УГЛОВ НАКЛОНА ПРЯМОЙ К ПЛОСКОСТЯМ ПРОЕКЦИЙ Длину отрезка АВ можно определить из прямоугольного треугольника АВС,где| AС | = A 1 B 1, | СB | = DZ, угол a - угол наклона отрезка к плоскости П1. Для этогона эпюре (рис. 21) из точки B 1 под углом 90° проводим отрезок B 1 B 10 = DZ, полученныйв результате построений отрезок A 1 B 10 и будет натуральной величиной отрезка АВ, а угол B 1 A 1 B 10 = α. Рассмотренный метод называется методом прямоугольного треугольника. Однако все построения можно объяснить, как вращение треугольника АВС вокруг стороны AС до тех пор, пока он не станет параллелен плоскости П1, в этом случае треугольник проецируется на плоскость проекций без искажения. Для определения b - угла наклона отрезка к плоскости П2 построения аналогичные (рис. 22). Только в треугольнике АВС сторона | ВС | = D U и треугольниксовмещается с плоскостью П2.
Обозначить проекции прямой и
Рис. 21
Обозначить проекции прямой и
Рис. 22 7 ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ Прямые в пространстве могут пересекаться, скрещиваться и быть параллельными. 1. Пересекающиеся прямые – это прямые, которые лежат в одной плоскости и имеют общую точку (a ∩ b = K). Теорема: Если в пространстве прямые пересекаются, то на чертеже пересекаются их одноименные проекции (рис. 23).
К = a ∩ b Þ К Î a; К Î b Þ К 1 = a 1 ∩ b 1; К 2 = a 2 ∩ b 2. Справедлива и обратная теорема: Если К 1 Î а 1; К 2 Î b 2 , то К 1 = а 1 ∩ b 1; К 2 = а 2 ∩ b 2 Þ К = а ∩ b.
2. Скрещивающиеся прямые – это прямые, которые не лежат в одной плоскости и не имеют общей точки (рис. 24). Пары точек 1 и 2, лежащие на горизонтально-проецирующей прямой называются горизонтально-конкурирующими, а точки 3 и 4 –фронтально-конкурирующими. По ним определяется видимость на эпюре.
Какая прямая будет видимой по отношению к плоскости П 2? 3. Параллельные прямые – это прямые, которые лежат в одной плоскости и имеют несобственную общую точку. Теорема:
Если k || m Þ k 1 || m 1, k 2 || m 2, k 3 || m 3
Справедлива обратная теорема: Если k 1 || m 1; k 2 || m 2 Þ k || m Лекция № 3 ПЛОСКОСТЬ 1. Способы задания плоскости на чертеже. Следы плоскости. 2. Положение плоскости относительно плоскостей проекций. 3. Принадлежность точки и прямой плоскости. 4. Главные (особые) линии плоскости.
1 СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ НА ЧЕРТЕЖЕ. СЛЕД ПЛОСКОСТИ Плоскость – бесконечная во все стороны линейчатая поверхность, которая на всем своем протяжении не имеет кривизны и преломления. Плоскость на чертеже может быть задана: 1. Тремя точками, не лежащими на одной прямой – Р (A, B, C), рис. 26. 2. Прямой и точкой, не лежащей на этой прямой –Р (m, A; A Ï m), рис. 27. 3. Двумя пересекающимися прямыми– Р (a ∩b), рис. 28. 4. Двумя параллельными прямыми– Р (a êê b), рис. 29. 5. Плоской фигурой (многоугольником, окружностью, эллипсом и др.)– Р ( D ABC), рис. 30. 6. Следами.
Рис. 26 Рис. 27 Рис. 28
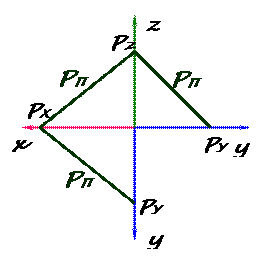
Рис. 29 Рис. 30 Задание плоскости следами След плоскости – линия пересечения плоскости с плоскостью проекций (рис. 31). Горизонтальный след получается при пересечении плоскости Р с горизонтальной плоскостью проекций (РП1 = Р ∩П1). РП2 = Р ∩П2 – фронтальный след;
Р x, Р y, Р z – точки схода следов.
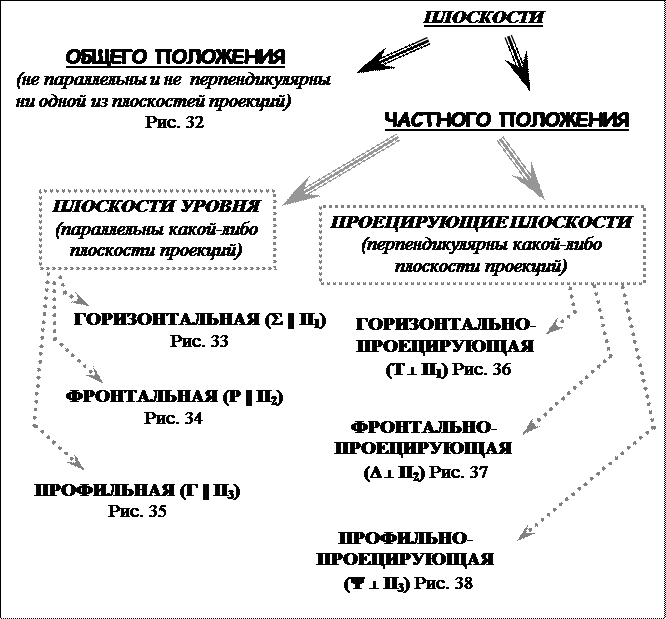
2 ПОЛОЖЕНИЕ ПЛОСКОСТИ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Плоскость относительно плоскостей проекций может занимать как общее, так и частные положения.
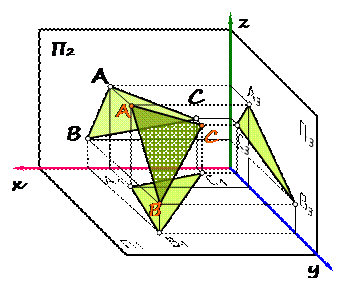
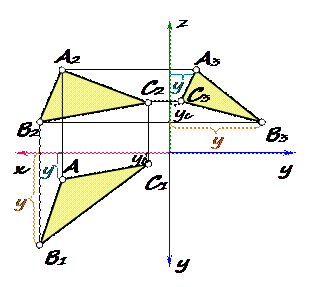
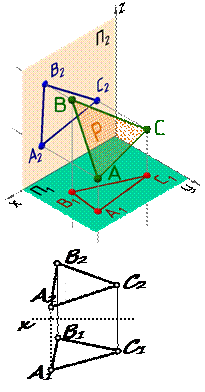
Плоскость общего положения на рис. 32 задана плоской фигурой – треугольником АВС. На все плоскости проекций треугольник проецируется с искажением.
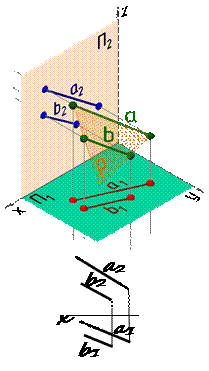
Рис. 32 Горизонтальная плоскость на рис. 33 задана следами. Плоскость имеет фронтальный и профильный следы, перпендикулярные оси z. Фронтальная и профильная проекции геометрических образов, лежащих в этой плоскости (например, точки и прямой), будут располагаться на соответствующих следах плоскости, а на горизонтальную плоскость проекций прямая спроецируется в натуральную величину.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 226; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.180.62 (0.012 с.) |

 скрещивание – •;
скрещивание – •;
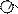 вращение –.
вращение –.
 S – центр проецирования
S – центр проецирования

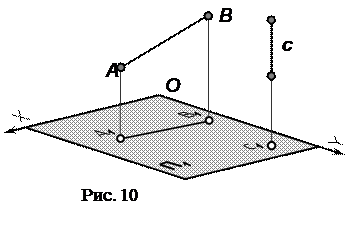 1 ПРЯМАЯ
1 ПРЯМАЯ
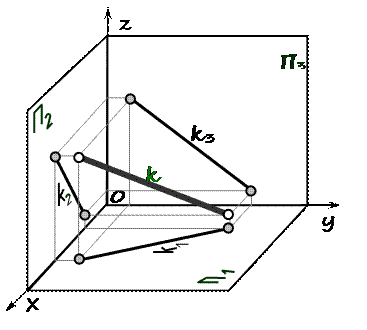 Проекция прямой общего положения меньше самой прямой.
Проекция прямой общего положения меньше самой прямой.
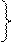 h 2 ïê 0 x признак
h 2 ïê 0 x признак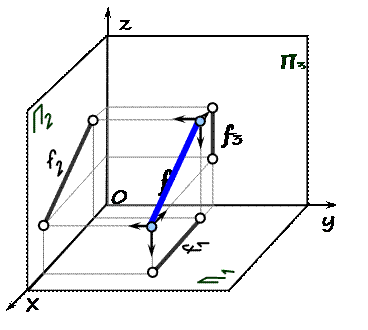
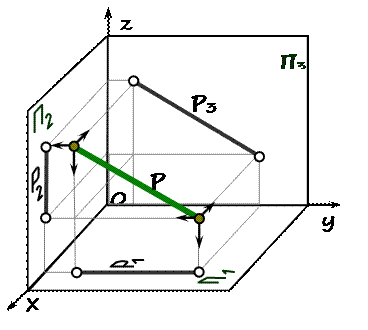
 g = 0°
g = 0°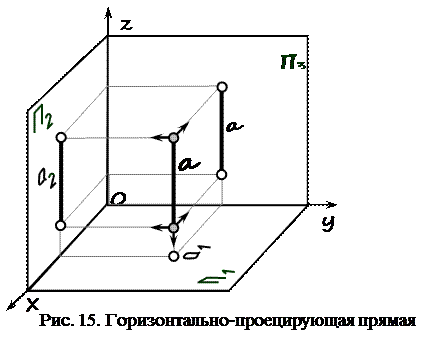
 а 2 ^ 0 х признак
а 2 ^ 0 х признак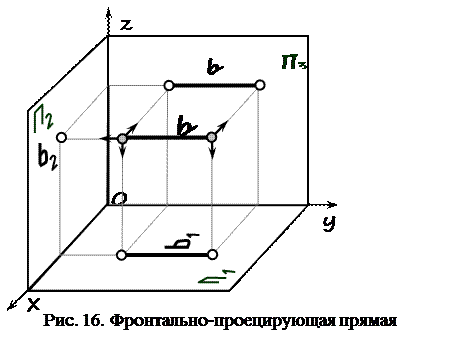
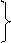 b 1 ^ 0 х признак
b 1 ^ 0 х признак
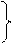 c 1 ^ 0 у признак
c 1 ^ 0 у признак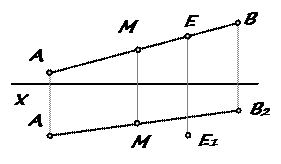 Теорема: Если в пространстве точка принадлежит прямой, то на эпюре проекции этой точки находятся на одноименных проекциях прямой (рис. 18):
Теорема: Если в пространстве точка принадлежит прямой, то на эпюре проекции этой точки находятся на одноименных проекциях прямой (рис. 18):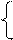 обозначить на H = k ∩ П 1 – горизонтальный след
обозначить на H = k ∩ П 1 – горизонтальный след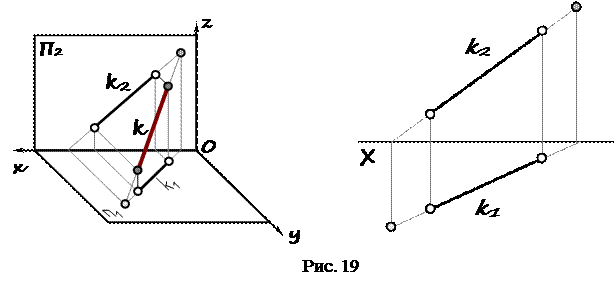


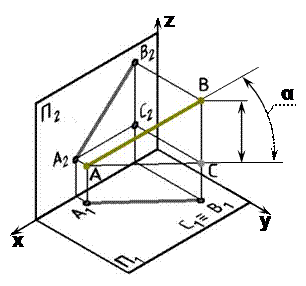
 определить угол α.
определить угол α.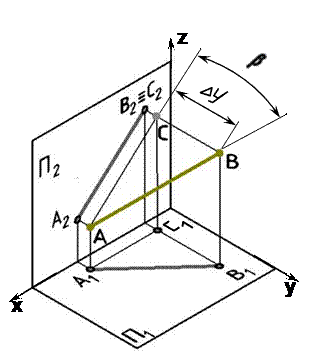
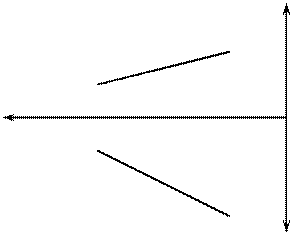 определить угол β.
определить угол β.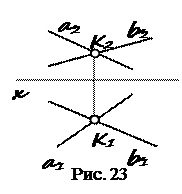 Точка пересечения одноименных проекций находится на одном перпендикуляре к оси Х (К 1 К 2 ^ О х).
Точка пересечения одноименных проекций находится на одном перпендикуляре к оси Х (К 1 К 2 ^ О х). По горизонтально-конкурирующим точкам 1 и 2 определяется видимость относительно П1. Точка 1 ближе к глазу наблюдателя, она будет видима на плоскости П1. Так как точка 1Î m, то прямая m будет выше прямой n.
По горизонтально-конкурирующим точкам 1 и 2 определяется видимость относительно П1. Точка 1 ближе к глазу наблюдателя, она будет видима на плоскости П1. Так как точка 1Î m, то прямая m будет выше прямой n. Если в пространстве прямые параллельны, то на чертеже параллельны их одноименные проекции (рис. 25).
Если в пространстве прямые параллельны, то на чертеже параллельны их одноименные проекции (рис. 25).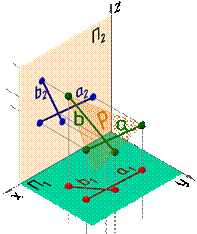 Каждый из указанных способов задания плоскости может быть преобразован в другой.
Каждый из указанных способов задания плоскости может быть преобразован в другой.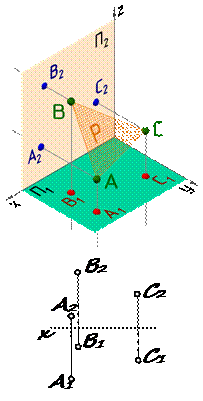


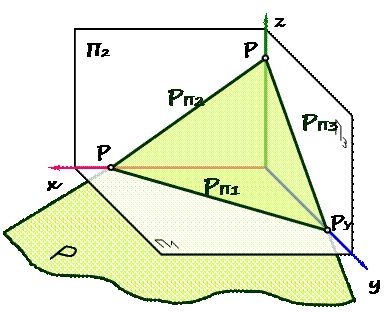 РП3 = Р ∩П3 – профильный след;
РП3 = Р ∩П3 – профильный след;