
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Растровая развертка окружностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
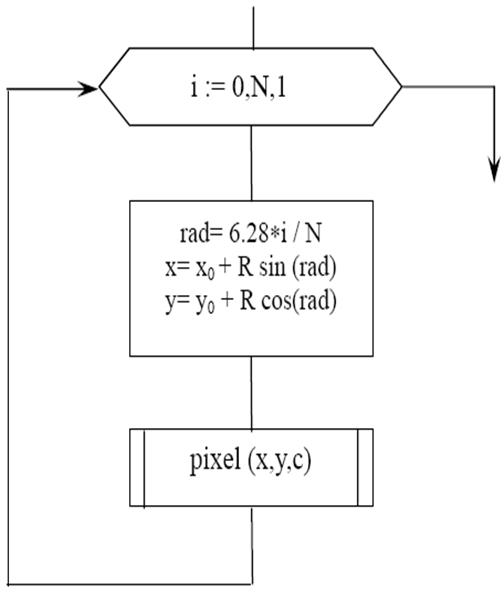
Построения окружностей и эллипсов можно осуществлять двумя способами: 1) используя уравнения тригонометрии и аналитической геометрии; 2) с использованием численных методов. Построение окружности с использованием аналитических выражений. В простейшем случае отображение окружности в растр можно осуществить при помощи аналитической зависимости между координатами X и Y. Алгоритм будет иметь вид:
Данный алгоритм легко модернизировать для случая построения эллипса. Необходимо заменить радиус R в уравнениях для вычисления координат на полуоси Rx и Ry. Аналогичным образом можно учесть другое соотношение координат окружности вида: x2 + y2 = R2 Отсюда можно вычислить соответствующее значение у:
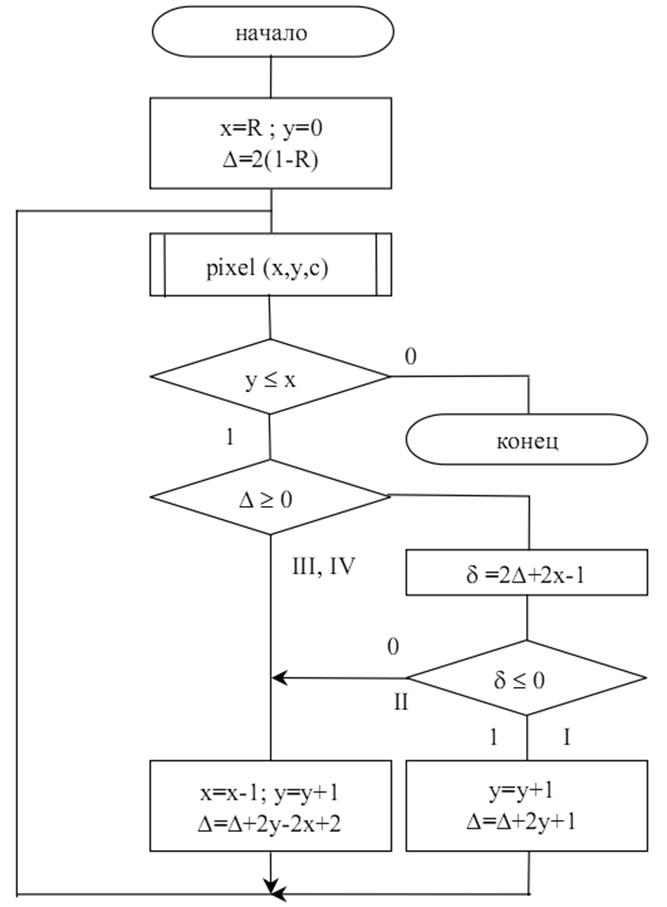
И в том и в другом случае алгоритм растровой развертки окружности достаточно прост для программирования, однако, его вычислительная сложность слишком велика для реализации в составе ядра базовой графической системы. Это объясняется наличием тригонометрических функций в первом случае и степенных – во втором. Поэтому использовать подобные процедуры или функции в составе базовой графической системы не целесообразно. Необходимо разработать такие алгоритмы, которые бы максимально эффективно выполняли растровую развертку окружности при минимальной вычислительной сложности. Один из них приведен ниже. Конец 19 вопроса. Брезенхемом был предложен алгоритм аппроксимации разложения окружности в растр, использующий целочисленную арифметику. Кроме отказа от длинных операций и сложности арифметических вычислений трудоемкость этого алгоритма можно сократить в 8 раз, если учесть симметричный характер окружности. Рассмотрим окружность, центр которой расположен в начале координат. При элементарных изменениях можно получить алгоритм, отображающий окружность в произвольном положении. Окружность имеет бесконечное множество осей симметрии, однако, для практики важно наличие восьмисторонней симметрии. Достаточно вычислить величины координат одной точки (х, у), после чего без дополнительных вычислений можно вывести на экран еще 7 точек (см. рис.4.6).
Рассмотрим реализацию алгоритма Брезенхема в первом октанте, так как на основании точек первого октанта можно восстановить всю окружность. В качестве начальной точки изображения выберем точку с координатами (R,0), где R – радиус разлагаемой в растр окружности (см. рис.4.7).
Для любой точки с произвольными координатами (xi, yi), находящейся на окружности при построении в выбранном направлении возможны два варианта перехода от текущего аппроксимирующего пиксела к следующему (см. рис.4.8). При этом координаты очередного аппроксимирующего пикселя составят следующие значения: (xi, yi) → (xi, yi + 1) - в вертикальном направлении; (xi, yi) → (xi - 1, yi + 1) - в диагональном направлении. Аппроксимирующий пиксель необязательно будет попадать на окружность радиуса R. Он может находиться либо ближе, либо дальше от центра окружности, т. е. радиус аппроксимирующей окружности может отличаться от радиуса исходной окружности. При этом отличие может изменяться от шага к шагу. Выберем в качестве меры отклонения радиусы между квадратами радиусов исходной и аппроксимирующей окружностей. Таким образом, зная координаты точки аппроксимации, можно определить конкретное отклонение окружности на каком-либо i-том шаге: Для того, чтобы выбрать направление перехода (либо в вертикальном, либо в горизонтальном направлении), необходимо оценить отклонения от исходного радиуса в этих двух случаях и сравнить их между собой. При переходе в вертикальном направлении на следующем шаге получим При переходе в диагональном направлении:
В случаях I и II получается, что Ra< R, т.е. аппроксимирующие точки лежат внутри аппроксимирующей окружности. В третьем случае Ra=R (точка аппроксимации лежит на окружности). В IV случае Ra>R, т.е. все аппроксимирующие точки находятся дальше от центра. Таким образом, для случаев I и II можно выбрать
Следовательно, определить величину ∆ можно, осуществив выбор очередной точки аппроксимации. Остается разделить варианты I и II. Рассмотрим каждый из этих случаев отдельно.
Вариант I
Вариант II Возможен выбор между точками V и D (рис.4.11).
Конец 20 вопроса. Задача, определяющая принадлежности точки замкнутому контуру, в общем случае является очень трудоемкой задачей, поэтому для уменьшения вычислительных затрат при обработке подобного контура рассматривается не вся рабочая поверхность экрана, а его ограниченная часть, называющаяся охватывающим прямоугольником.
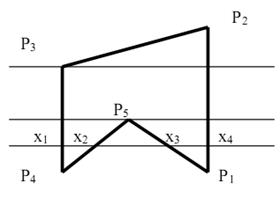
Координаты углов охватывающего прямоугольника определяются максимальными и минимальными значениями координат X и Y рассматриваемого контура. Для того чтобы эффективно реализовать процедуру развертки сплошной области, необходимо воспользоваться двумя дополнительными процедурами: 1) определение когерентности растровых строк; 2) сортировка. Под когерентностью понимается пространственная однородность характеристик пиксела в сканируемой строке. Изменение характеристик пиксела свидетельствует о достижении границы контура. Как правило, на практике описание ломаной линии контура хранится в неупорядоченном виде (см. рис.4.14).
Если многоугольник задан ребрами, то точки пересечений строки растровой развертки будут располагаться не упорядоченно. Для нашего случая (рис.4.14): (p1, p2), (p2, p3), (p3, p4), (p4, p5), (p5, p1) < x4, x1, x2, x3 >. Для того, чтобы получить координаты интервала заполнения строки в растре развертки, необходимо выполнить сортировку множества точек пересечения < x1, x2, x3, x4 >. Таким образом, алгоритм выполнения сортировки является неотъемлемой частью ядра базовой графической системы. При выполнении построения растровой развертки особой обработки требуют вершины многоугольного контура. Возможны два случая: 1) в том случае, если вершина контура является локальным экстремумом, то она учитывается в списке два раза (например, P5); 2) в противном случае, она учитывается один раз (например, P3). Для повышения эффективности вычислительной процедуры сортировки по строкам и сортировки в строке выполняются раздельно. Простейшим вариантом алгоритма данной группы является алгоритм с упорядоченным списком ребер. Он состоит из двух частей: 1) подготовительная (шаги 1 – 3); 2) собственно развертка (шаги 4 – 5). Алгоритм растровой развертки с упорядоченным списком ребе 1. Для каждого ребра контура определить точки пересечения со строками развертки, используя алгоритм Брезенхейма. 2. Поместить координату X точки пересечения в соответствующую группу описания строки (Y – группу) 3. Для каждой строки выполнить сортировку множества координат X точек пересечения (в порядке возрастания). 4. Для каждой строки развертки сгруппировать попарно X – координаты точек пересечения. 5. Активизировать пиксели текущей строки развертки в пределах пар X – координат. Данный алгоритм является простым и очевидным, однако требует большого объема памяти, который уходит на хранение точек пересечения всех ребер со всеми строками растра. На практике можно значительно сократить объем необходимой памяти, если учитывать регулярный характер граней, образующих контур. Для ускорения вычисления и уменьшения объема памяти используется: 1) структурирование данных в виде связного списка ребер; 2) вычисление координат точек пересечения в пошаговом режиме.
На использовании данных приемов базируется следующий вариант алгоритма растровой развертки сплошных областей - алгоритм с активным списком ребер. Алгоритм растровой развертки сплошных областей, использующих список активных ребер (САК). Алгоритм также состоит из двух частей: подготовительной (1 – 3) и растровой развертки (4 – 13). 1. Для каждого ребра многоугольника определить Y – координату с максимальным значением. 2. Сформировать для каждой строки Y – группу и занести выделенные ребра в соответствующие группы. 3. Сформировать связный список, сохранив в нем следующие значения: а) начальная величина координаты Х точек пересечения; б) ∆y – число строк, пересеченных ребром, уменьшенное на единицу; в) ∆х – шаг приращения по Х – координате при переходе на одну строку; г) указатель на данные следующего активного ребра, начинающегося на данной строке развертки. 4. Для каждой строки развертки проверить соответствующую Y – группу на наличие новых ребер. 5. Добавить новые ребра в САК. 6. Выполнить сортировку координат Х точек пересечения ребер, входящих в САК в порядке возрастания. 7. В отсортированном списке выделить пары точек пересечения. 8. Активизировать на строке растра пикселы с координатами, входящими в отрезки, определенные на шаге 7. 9. Для каждого ребра из САК уменьшить ∆y на единицу. 10. Если ∆y < 0, исключите данное ребро из САК. 11. Вычислить новое значение Х – координаты точки пересечения. 12. Перейти к следующей строке. 13. Если область, охватывающего прямоугольника просмотрена (y < ymin), то завершаются вычисления, иначе возврат к п.4.
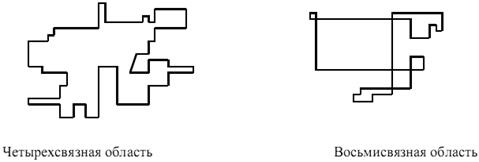
Конец 21 вопроса. Алгоритмы данной группы предполагают, что известен хотя бы один пиксел принадлежащий внутренней области окрашеваемого многоугольника. Существует множество различных видов областей, которые можно разделить на следующие группы: 1) по характеру границ: - внутренне определенные; - гранично определенные; 2) по характеру связности внутренних точек области: - четырехсвязные; - восьмисвязные. Гранично определенные области, в отличие от внутренне определенных, имеют на границе области пиксели выделенного цвета (контур). Связность областей определяется количеством направлений перемещения внутри заполняемой области (рис.4.17).
Алгоритмы, ориентированные на заполнение восьмисвязных областей, способны заполнять любую четырехсвязную область, однако обратное не всегда верно.
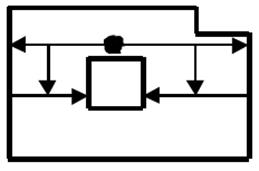
Рассмотрим простейший вариант алгоритма, ориентированного на заполнение четырехсвязных областей. При работе алгоритма используется стек, хранящий затравочные пиксели. Для работы со стеком необходимы две процедуры -запись данных (координат пикселей) (PUSH) и чтение данных из стека (POP). В алгоритме последовательно проверяются и помещаются в стек пиксели четырехсвязной области. Алгоритм начинает работать с исходного затравочного пикселя (x0,y0), а четыре связанные с ним пикселя рассматриваются, начиная с правого от текущего, и далее против часовой стрелки. Алгоритм представляет из себя итерационную процедуру, на каждом шаге которой происходит извлечение очередного затравочного пикселя из стека. Этот пиксель отображается, после чего в стек помещаются (при наличии) связанные с ним пиксели. В стек помещаются только те пиксели, которые не окрашивались на предыдущих шагах. Итерационный цикл завершается, когда стек оказывается пустым. Рассмотрим работу данного алгоритма на примере. Пусть задана область (см. рис.), имеющая границу определенного цвета, и известен пиксель внутри нее, который выбирается как затравочный.
Данный алгоритм легко модернизировать для восьмисвязных областей. Кроме того его можно оптимизировать, уменьшив объем стека, используемого в ходе закраски области. Следует отметить, что появление на приведенном рисунке в отдельных пикселях нескольких чисел, определяющих положение координат пикселя в стеке, свидетельствует о том, что происходит дублирование информации, т.е. один и тот же пиксель несколько раз помещается в стек. Это снижает эффективность алгоритма. Поэтому при написании программной реализации алгоритма с затравкой стараются исключить повторное занесение пикселя в стек. Данный алгоритм ориентирован на заполнение достаточно сложных областей четырех- или восьмисвязной конфигурации. Подобные области часто не могут быть заполнены при помощи алгоритмов построчной развертки. В этом плане они эффективнее. Однако, в связи с тем,что в данной группе алгоритмов происходит попиксельная обработка, они значительно медленнее работают. Поэтому в плане производительности данная группа алгоритмов менее эффективна. С целью соединить достоинства двух групп алгоритмов заполнения многоугольников разработана третья группа алгоритмов, которые называются алгоритмами построения развертки с затравкой. В алгоритмах данной группы осуществляется минимизация размеров стека за счет хранения одного затравочного пикселя для каждой строки развертки и заполнение каждой строки развертки влево и вправо от затравочного пикселя до достижения границ области.
При заполнении областей, имеющих сложные конфигурации, возникают проблемы при наличии разрывов в областях. В этом случае после проведения развертки текущей строки необходимо выполнить проверку заполненности всех пикселей предыдущей строки развертки.
Для реализации подобной проверки используются как точные алгоритмы, базирующиеся на графических моделях, так и эвристические,позволяющие с большой точностью выполнять закраску области сменьшими проверками за меньшее время.
Конец 22 вопроса. При отсечении на плоскости выполняется, с одной стороны, выделение обрабатываемой области экрана, а с другой стороны, объекты этой выделенной области разбиваются на составляющие. Для операции отсечения элементарным геометрическим объектом является линия (отрезок прямой). Существует ряд алгоритмов, позволяющих оптимизировать процесс отсечения, но наиболее эффективно реализован на методе кодирования, предложенном американскими инженерами Коэнном и Сазерлен дом (Cohen D., Sutherland I.). Для быстрого определения видимости/невидимости отрезков прямых был предложен способ четырехразрядного кодирования. Каждый разряд этого кода определяет принадлежность концов отрезка к соответствующим областям. Если точка попадает в область, то код равен единице.
Используя эти коды можно определить видимость (полную или неполную) или невидимость отрезка. Рассмотрим возможные варианты кодировки концевых точек: 1) С1=С2=0 – отрезок полностью видим (обе точки внутри окна); 2) если хотя бы одна из точек имеет и отличие от 0, то, следовательно, часть отрезка или он полностью невидим: 2.1) если поразрядное логическое произведение кодов отлично от нуля (С1&С2 ≠0), то отрезок полностью невидим; 2.2) С1&С2 = 0, то отрезок может быть как видимым, так и невидимым. В этом случае выполняется дополнительный анализ, при котором концевые точки заменяются точками пересечения рассматриваемого отрезка с границами отсекающего окна. Алгоритм Коэнна - Сазерленда Этот алгоритм выполняется следующим образом: для каждой стороны окна выполнить: для каждого отрезка выполнить следующие действия: проверка С1 = С2 = 0; если результат проверки положительный, то - отобразить отрезок, иначе - выполнить: если С1&С2 ≠0, то перейти к следующему отрезку, иначе заменить точки Р1 и Р2 на точки пересечения отрезка с границами окна. Конец 23 вопроса. Многоугольник можно рассматривать как замкнутую последовательность отрезков, расположенных на плоскости, а операцию отсечения реализовать с точки зрения вычисления взаимного перекрытия двух многоугольников. Один из многоугольников представляет собой отсекающее окно, а другой – отсекаемый объект. При реализации подобных алгоритмов на базе вычислений пересечений, возникает ряд проблем, связанных с тем, что фигура отсекаемого многоугольника может превратиться в набор разрозненных отрезков, либо в открытые многоугольники (как на рис.4.24).
Для устранения подобных ситуаций существует ряд алгоритмов которые отличаются исходными данными, характером просмотра пересечений, а также ограничениями на вид отсекаемого и отсекающего многоугольника. Простейшим вариантом является алгоритм ориентированный на регулярные формы многоугольника (стороны многоугольника параллельны осям координат или границам экрана). Алгоритм Сазерленда-Ходжмена. Алгоритм Сазерленда-Ходисмена основан на последовательном отсечении рёбер многоугольника каждой из границ отсекающего окна. Например:
Реальный алгоритм более сложен, т.к. учитывает произвольную форму и ориентацию, как отсекаемого многоугольника, так и отсекающего окна. Исходными данными для работы алгоритма являются списки вершин многоугольника и отсекающего окна v1,v2,…,vn; w1,w2,…,wn. Работа алгоритма заключается в последовательном просмотре вершин многоугольника с вычислением координат пересечений границ окна с рёбрами многоугольника, а также в формировании результирующей фигуры. Как правило, алгоритм реализуется за два этапа. На первом этапе в прямой последовательности осуществляется просмотр вершинv1,v2,…,vn и выявляются точки пересечения. На втором этапе осуществляется обратный просмотр с формированием выходного списка отсечённого многоугольника. При этом на каждом шаге работы алгоритма могут быть занесены 1,2 – вершины. Проанализируем варианты пересечения границы окна с ребром многоугольника.
Перед началом работы цикла выбирается начальная точка v1внутри. Случай 1. Ребро полностью находится внутри окна. При этом начальная точка v1 ребра находится в выходном списке, а вторая вершина v2 добавляется в список. Случай 2. Ребро выходит за пределы окна. При этом известна точка пересечения x1 ребра с окном. В выходной список заносится точка пересечения x1. Случай 3. Ребро полностью находится за пределами окна. В этом случае выходной список не изменяется. Случай 4. Ребро входит в окно, и в выходной список заносятся две точки: точка пересечения x2 и v1. Данный алгоритм позволяет работать как с выпуклыми, так и с не выпуклыми многоугольниками. Алгоритм может быть реентерабельным, т.е. может обращаться сам к себе. В этом случае отсутствует требование к дополнительной памяти. Поэтому такой алгоритм может быть реализован аппаратно. Хотя исходный вариант алгоритма ориентирован на плоскость, при незначительной модернизации он может быть переориентирован в пространство. Алгоритм Вейлера – Азертона. Данный алгоритм ориентирован на эффективное решение проблемы отсечения в том случае, если в результате отсечения образуется множество ребер на границе окна. Внесение простейших изменений в элементарный алгоритм отсечения не дает эффективных решений, поэтому был предложен данный алгоритм, базирующийся на просмотре списка верши и специальных правил обхода контуров. В алгоритме Вейлера – Азертона происходит отслеживание перемещения вдоль границ многоугольника в выбранном направлении (например, по часовой стрелке) вплоть до пересечения с границей окна. После определения факта пересечения осуществляется анализ варианта пересечения: 1) если ребро входит в окно, то просмотр продолжается вдоль ребра многоугольника; 2) если ребро выходит из окна, то выполняется поворот по границе окна в выбранном направлении. В любом случае точка пересечения запоминается и используется как точка возврата для продолжения обхода многоугольника.
Конец 24 вопроса. Алгоритмы трехмерного отсечения, или алгоритмы удаления невидимых линий и поверхностей, служат для формирования результирующего изображения в различных программах трехмерного моделирования. Эти алгоритмы относятся к основным алгоритмам ядра графических систем. Алгоритмы трехмерного отсечения можно разделить на две большие группы: 1) алгоритмы, работающие в пространстве объектов; 2) алгоритмы, работающие в пространстве изображений. Алгоритмы, как первой, так и второй групп обязательно включают в себя алгоритмы сортировки, а также некоторые специальные алгоритмы, например, тесты взаиморасположения объектов. Алгоритмы, работающие в пространстве объектов используют систему координат моделируемых объектов. Это позволяет добиваться высокого качества результатов. Однако они предъявляют повышенные требования к вычислительным ресурсам, поэтому подобные алгоритмы используются в промышленных САПР, а также в системах трехмерного моделирования, ориентированные на высокое качество изображений для кино- и видео-индустрии (AUTOCAD, ARCHICAD, MAYA и т.п.). Алгоритмы, работающие в пространстве изображений работают с системой координат экрана, которая и определяет точность и качество полученного результата. К данному классу относят программы, работающие с плоскими изображениями 2D и 2.5D. Примером являются современные системы нелинейного видеомонтажа и простейшие системы моделирования. Алгоритм Варнока Данный алгоритм работает по тому же самому принципу, по которому осуществляет обработку информации зрительная система человека и его головной мозг. При этом исходное изображение сегментируется, то есть делится на отдельные области, которые отличаются своей когерентностью (однородностью), и которые сортируются по показателям их информационной ёмкости. В результате подобной предварительной обработки представляется возможность затрачивать наибольшее время на работу с высокоинформативными частями изображения. Малоинформативные части изображения могут быть в предельном случае вообще отброшены. Реальный алгоритм Варнока ориентирован на организацию в пространстве изображений. При этом для повышения эффекта его реализации его можно непосредственно реализовать в видеобуфере системы. Алгоритм Варнока является итерационным алгоритмом, в результате действий которого происходит деление исходного окна на подокна. При делении могут быть использованы различные признаки. Если полученное на определённом шаге окно не является когерентным, то оно делится на отдельные фрагменты, каждый из которых рассматривается в качестве самостоятельного окна на следующем шаге итерации. Дробление окон осуществляется до тех пор, пока изображение не станет достаточно простым, либо его размеры достигнут минимального предела. В последнем случае информация в выделенном окне усредняется, и результат изображается в виде одного пикселя, имеющего усреднённые атрибуты. При этом следует учитывать, что минимальные объекты (пиксели) воспринимаются человеческим зрением в большей степени по их яркости (цветовые показатели играют второстепенную роль). В ходе выполнения алгоритма можно осуществить устранение реалистичного эффекта, доведя процесс разбиения до размеров, меньших, чем разрешение экрана, производится усреднение атрибутов этого объекта и отображение его в виде пикселя. Существует множество различных реализаций алгоритма Варнока, которые отличаются друг от друга, во–первых, методом разбиения окна, а во–вторых, критерием, используемым для определения процесса завершения итерации. В оригинальном алгоритме исходное окно(256°256) разбивалось на четыре одинаковых подокна. В этом случае для достижения окончательного разбиения требуется не более восьми шагов (28 = 256). Для повышения эффективности работы алгоритма могут использоваться другие принципы разбиения, например: 1) разбиение по крайним точкам объекта; 2) разбиение вдоль границ объекта. Для того, чтобы определить когерентность области используется ряд тестов, базирующихся на анализе взаимного расположения окна и отсекаемых объектов. В алгоритме Варнока рассматривается четыре варианта расположения отсекаемых многоугольников и отсекающегоокна: 1) внешнее расположение; 2) внутреннее расположение; 3) пересекающее расположение; 4) охватывающее расположение. Для выполнения этого теста используется следующее правило обработки окон: 1) если все многоугольника моделируемой сцены являются внешними, то окно пусто и отображается цветом фона; 2) если внутри окна находится только один многоугольник, то его можно считать достаточно простым для отображения и заполнять цветом фона, на который накладывается многоугольник; 3) если окно пересекает только один многоугольник, то его также можно рассматривать как когерентное окно, и, определив отсечения многоугольника, сводят данный случай к правилу 2; 4) если окно охвачено только одним многоугольником, то оно считается когерентным и заполняется цветом этого многоугольника; 5) если отсекающее окно охватывает несколько многоугольников, то среди них выбирается ближний, и данный случай сводится к правилу 4. Во всех остальных случаях необходимо выполнить разбиение окна. Для определения взаимного расположения отсекающего окна и многоугольников существует несколько тестов. Простейший из них – габаритный. Он легко реализуется, однако при усложнении форм многоугольника даёт неверный результат.
Для работы с многоугольниками сложных форм наиболее эффективным оказывается другой тест – тест с бесконечным лучом (рис.4.31). При выполнении данного теста из любой точки окна (чаще из угла) проводится луч и осуществляется отсчёт числа данного пересечения луча с многоугольником. Если это число – чётное, то рассмотренный многоугольник является внешним, а если нечётное – охватывающим (рис.4.32). Отдельно учитываются точки пересечения с вершинами многоугольника. Если луч касается вершины, значение счётчика увеличивается на два. В том случае, если луч пронзает вершину, значение счётчика увеличивается на единицу (вместо счётчика можно использовать логический флаг).
Существуют более сложные наиболее точные тесты, базирующиеся, например, на подсчёте суммы углов многоугольника. Конец 25 вопроса. Данный алгоритм относится к другой группе алгоритмов отсечения, так как работает в пространстве объектов. Для повышения эффективности (уменьшения количества шагов разбиения) осуществляется дробление окон вдоль границ многоугольника. Алгоритм Вейлера-Азертона на одноименном двухмерном алгоритме. Трехмерный алгоритм реализуется за четыре этапа: 1) предварительная сортировка по глубине (z-сортировка); 2) сортировка многоугольников на плоскости (x,y-сортировка); 3) удаление экранированных многоугольников; 4) рекурсивное разбиение и окончательная сортировка при наличии неопределенности. ЭТАП 1. Z-сортировка.
ЭТАП 2. X,Y-сортировка. На данном этапе происходит сортировка в плоскости экрана. В результате создается два списка многоугольников: А) внутренний (для многоугольников, попадающих в окно) Б) внешний (для всех прочих). Для отсечения используется копия ближайшего многоугольника, определенного на первом этапе.
Поскольку отсечение производится ближайшим многоугольником, то первым во внутреннем списке является он сам. ЭТАП 3.
При выполнении проверки для каждой j-ой вершины i-ого многоугольника с координатами (Xij, Yij), отсекаемого ближайшим многоугольником, определяется глубина Zij. Затем Zij сравнивается с глубиной Zk ближайшего многоугольника, зафиксированного при z-сортировке. Если вычисленная величина Zij< Zk, то порядок, определенный z-сортировкой, правильный. В том случае, если Zij > Zk, то результат z-сортировки – ошибочен. В первом случае продолжается рекурсивная работа с внешним списком многоугольников. Во втором случае – необходим переход к четвертому этапу. ЭТАП 4. Необходимость в нем возникает в том случае, если среди Zij есть значение, большее Zk. Такой многоугольник, по крайней мере, частично экранирует ближайший многоугольник, определенный на первом этапе. Для устранения ошибки сортировки осуществляется рекурсивное разбиение X,Y-плоскости с использованием в качестве отсекающего того многоугольника, который нарушил правило сортировки по z-координате. Отсечению подлежат многоугольники из внутреннего списка, в том числе и старый ближайший многоугольник. Для отсечения используется копия нового претендента. Данный алгоритм обрабатывает случаи циклического перекрытия нескольких многоугольников.
Конец 26 вопроса. Данный алгоритм был предложен Ньюэллом и Санчем. При работе исполняется понятие оболочек геометрических объектов. В общем случае в качестве n - мерной оболочки подразумевается n - мерный параллелепипед, размеры которого соответствуют габаритным размерам исходного объекта.
Данный вариант алгоритма позволяет сортировать многоугольники по их Z – координатам и реализуется за три шага: 1) упорядочивание многоугольника по координате Z – max; 2) разрешение неопределенностей при перекрытии Z-оболочек; 3) преобразование многоугольников в растровую форму. Для выполнения шага 2 исполняется тест, состоящий из 5 проверок. Рассмотрим ситуацию, при которой в качестве ближайшего многоугольника на первом шаге выбран многоугольник P. Многоугольник имеющий перекрытие Z оболочек с многоугольником Р обозначаем Q. Необходимо выполнить следующие пять проверок: 1) Х- оболочки не перекрываются; 2) У- оболочки не перекрываются; 3) многоугольник Р целиком за плоскостью Q; 4) многоугольник Q целиком перед плоскостью Р; 5) ХУ- оболочки многоугольников Р и Q не перекрываются. Если во всех пяти случаях получается отрицательный ответ, то Р закрывает Q, в противном случае Q закрывает Р, поэтому в первоначальном списке многоугольники Р и Q необходимо поменять местами Данный алгоритм не позволят обрабатывать в случае взаимного перекрытия объектов, этот вариант приводит к зацикливанию алгоритма
Для устранения данного недостатка осуществляется контроль за моментом возникновения зацикливания, для этого фиксируются многоугольники, входящие в список конфликтов. Зацикливание образуется при повторном вхождении многоугольников в список. Для того чтобы разорвать подобный цикл, многоугольник, повторно возникший в этом списке, делят на две части, таким образом, чтобы не возникало конфликтов между многоугольниками. Данный алгоритм часто называют «алгоритмом художника». Егос ложность определяется Q (n2), где n – количество многоугольников.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1137; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.211.58 (0.02 с.) |



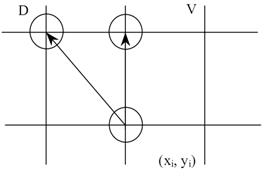

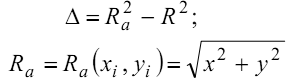



 Вычисления по формулам (4.2) – (4.4) содержат квадраты чисел поэтому желательно упростить эти выражения. Этого можно добиться если рассмотреть конкретные возможные варианты пересечения линий окружности с сеткой растра. В первом октанте возможны следующие четыре вида пересечений линий окружности и сетки растра (рис. 4.9).
Вычисления по формулам (4.2) – (4.4) содержат квадраты чисел поэтому желательно упростить эти выражения. Этого можно добиться если рассмотреть конкретные возможные варианты пересечения линий окружности с сеткой растра. В первом октанте возможны следующие четыре вида пересечений линий окружности и сетки растра (рис. 4.9).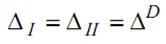













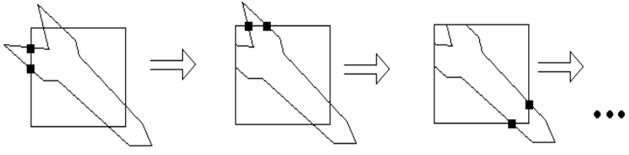




 На этом этапе происходит формирование списка приблизительных приоритетов, определяющего в первом приближении удаленность многоугольников от наблюдателя. Если за точку наблюдения принимать z=+∞, то ближайший многоугольник должен иметь максимальную z-координату. Построение списка приблизительных приоритетов осуществляется путем сохранения z-координат для каждого из многоугольников.
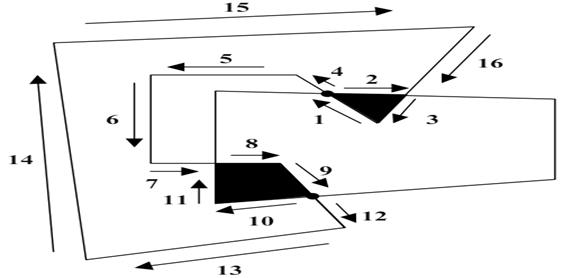
На этом этапе происходит формирование списка приблизительных приоритетов, определяющего в первом приближении удаленность многоугольников от наблюдателя. Если за точку наблюдения принимать z=+∞, то ближайший многоугольник должен иметь максимальную z-координату. Построение списка приблизительных приоритетов осуществляется путем сохранения z-координат для каждого из многоугольников.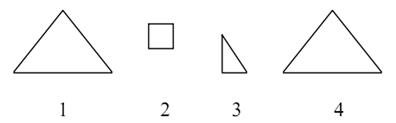
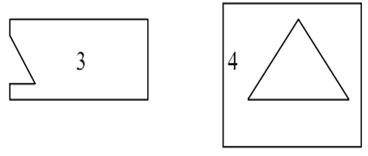
 На данном этапе выполняется полная проверка координат многоугольников, учитывая тот факт, что первоначальная z-сортировка является приблизительной.
На данном этапе выполняется полная проверка координат многоугольников, учитывая тот факт, что первоначальная z-сортировка является приблизительной.





