
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Курсовая работа по линейной алгебреСодержание книги
Поиск на нашем сайте
Курсовая работа по линейной алгебре И аналитической геометрии на тему: «Исследование кривых и поверхностей второго порядка» выполнил: студент группы 1202 Пелеванюк И.С. руководители: доцент Казача Г.С. доцент Шевцов В.Ф. Дубна, 2008 Оглавление
Введение Постановка задачи 1. Общая теория кривых второго порядка 1.1 Кривые второго порядка 1.2 Классификация кривых второго порядка 2. Исследование кривой второго порядка 2.1 Определение зависимости типа кривой от параметра с помощью инвариантов 2.2 Построение кривых при различных значениях параметра 2.3 Приведение уравнения кривой при β = 0 к каноническому виду 2.4 Определение эксцентриситета, фокусов, директрис, асимптот данной кривой второго порядка 2.5 Построение кривой второго порядка в общей и канонической системах координат 3.Общая теория поверхностей второго порядка 3.1 Поверхности второго порядка 3.2 Исследование формы поверхности второго порядка методом сечения плоскостями 4.Исследование поверхности второго порядка 4.1 Приведение уравнения поверхности к каноническому виду 4.2 Исследование формы поверхности методом сечений плоскостями 4.3 Построение поверхности в канонической системе координат Вывод Список используемой литературы
Введение Постановка задачи Задание 1. Для данного уравнения кривой второго порядка с параметром
1. Определить зависимость типа кривой от параметра β с помощью инвариантов. 2. Построить кривые всех возможных типов для данного уравнения с параметром. 3. Привести уравнение кривой при β = 0 к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей. 4. Найти фокусы, директрисы, эксцентриситет и асимптоты (если они есть) данной кривой второго порядка. 5. Построить кривую в канонической и общей системах координат. Задание 2. Для данного уравнения поверхности второго порядка: . 1. Привести уравнение поверхности к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей. 2. Исследовать форму поверхности методом сечений и построить полученные сечения. 3. Построить поверхность в канонической системе координат. Общая теория кривых второго порядка Кривые второго порядка
Пусть кривая Г задана в декартовой прямоугольной системе координат xOy уравнением:
Если хотя бы один из коэффициентов Теорема 1. Для произвольной кривой второго порядка 1) 2) 3) 4) 5) 6) 7) 8) 9) В этих уравнениях a, b, p — положительные параметры. Систему координат XO ' Y назовем канонической системой координат, а систему координат xOy —общей системой координат. Функция
Значения Кривая поверхность порядок Определение эксцентриситета, фокусов, директрис, асимптот данной кривой второго порядка 1. Найдем фокусы. Для того чтобы найти фокусы гиперболы воспользуемся следующими формулами: F 1(– c, 0), F 2(c, 0), где
Следовательно, фокусы имеют вид: 2. Найдем эксцентриситет. Эксцентриситетом гиперболы называется величина
3. Найдем директрисы:
4. Найдем асимптоты по формуле:
Построение кривой второго порядка в общей и канонической системах координат Рис.6. Кривая в канонической системе координат
Рис.7. Кривая в общей системе координат Общая теория поверхностей второго порядка Поверхности второго порядка
Поверхностью второго порядка S называется геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида:
где, по крайней мере, один из коэффициентов Уравнение (4.1) называют общим уравнением поверхности второго порядка S,а систему координат Oxyz называют общей системой координат. Теорема:Для произвольной поверхности S, заданной общим уравнением (3.1), существует такая декартова прямоугольная система координат O ' XYZ что в этой системе поверхность S задана уравнением одного из следующих канонических видов: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) В вышеперечисленных уравнениях a, b, c, p — положительные параметры. Систему координат O ' XYZ называют канонической. Вывод
Таким образом, из вышеприведенного анализа следует, что, тип кривой второго порядка, заданной алгебраической формой, можно легко определить с помощью поворота осей и параллельного переноса начала координат. Так же из анализа следует, что зная знаки инвариантов, можно полностью определить тип линии второго порядка при различных значениях β, что мы и делаем. Четвёртая часть работы наглядно показывает, что исследование формы поверхности методом сечений плоскостями даёт хорошее представление о поверхности, которую мы исследуем. Данный способ исследования можно применять даже не зная, какая именно поверхность задана уравнением. Список используемой литературы 1. Бобылева Л. В., Брюхина Л. С. Линейная алгебра и аналитическая геометрия: Исследование кривых и поверхностей второго порядка: Учебно-методическое пособие — Дубна: Международный университет природы, общества и человека «Дубна», 2003. 2. Копылова Т. В. Аналитическая геометрия. — Дубна: Международный университет природы, общества и человека «Дубна», 1997
Размещено на Allbest.ru Курсовая работа по линейной алгебре И аналитической геометрии на тему: «Исследование кривых и поверхностей второго порядка» выполнил: студент группы 1202 Пелеванюк И.С. руководители: доцент Казача Г.С. доцент Шевцов В.Ф. Дубна, 2008 Оглавление
Введение Постановка задачи 1. Общая теория кривых второго порядка 1.1 Кривые второго порядка 1.2 Классификация кривых второго порядка 2. Исследование кривой второго порядка 2.1 Определение зависимости типа кривой от параметра с помощью инвариантов 2.2 Построение кривых при различных значениях параметра 2.3 Приведение уравнения кривой при β = 0 к каноническому виду 2.4 Определение эксцентриситета, фокусов, директрис, асимптот данной кривой второго порядка 2.5 Построение кривой второго порядка в общей и канонической системах координат 3.Общая теория поверхностей второго порядка 3.1 Поверхности второго порядка 3.2 Исследование формы поверхности второго порядка методом сечения плоскостями 4.Исследование поверхности второго порядка 4.1 Приведение уравнения поверхности к каноническому виду 4.2 Исследование формы поверхности методом сечений плоскостями 4.3 Построение поверхности в канонической системе координат Вывод Список используемой литературы
Введение Постановка задачи Задание 1. Для данного уравнения кривой второго порядка с параметром
1. Определить зависимость типа кривой от параметра β с помощью инвариантов. 2. Построить кривые всех возможных типов для данного уравнения с параметром. 3. Привести уравнение кривой при β = 0 к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей. 4. Найти фокусы, директрисы, эксцентриситет и асимптоты (если они есть) данной кривой второго порядка. 5. Построить кривую в канонической и общей системах координат. Задание 2. Для данного уравнения поверхности второго порядка: . 1. Привести уравнение поверхности к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей. 2. Исследовать форму поверхности методом сечений и построить полученные сечения. 3. Построить поверхность в канонической системе координат.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 757; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.238.6 (0.009 с.) |

 :
:
 . (1.1)
. (1.1) отличен от нуля, то кривую Г называют кривой второго порядка.
отличен от нуля, то кривую Г называют кривой второго порядка.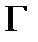 существует такая декартова прямоугольная система координат XO ' Y, что в этой системе кривая Г имеет уравнение одного из следующих каноническихвидов:
существует такая декартова прямоугольная система координат XO ' Y, что в этой системе кривая Г имеет уравнение одного из следующих каноническихвидов: , а ³ b >0— эллипс;
, а ³ b >0— эллипс; — мнимый эллипс;
— мнимый эллипс;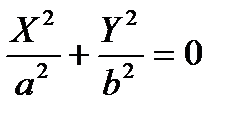 — две мнимые пересекающиеся прямые;
— две мнимые пересекающиеся прямые; — гипербола;
— гипербола; — две пересекающиеся прямые;
— две пересекающиеся прямые; — парабола;
— парабола; — две параллельные прямые;
— две параллельные прямые;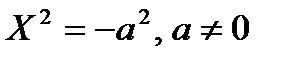 — две мнимые параллельные прямые;
— две мнимые параллельные прямые; — две совпадающие прямые.
— две совпадающие прямые. называется квадратичной формой, соответствующей уравнению (1.1).
называется квадратичной формой, соответствующей уравнению (1.1). ,(1.2)
,(1.2) .(1.3)
.(1.3) (1.4)
(1.4) не меняются при переходе от одной декартовой прямоугольной системы координат к другой, полученной в результате поворота осей координат и переноса начала координат, то есть являются инвариантамикривой Г относительно поворота осей координат и переноса начала.
не меняются при переходе от одной декартовой прямоугольной системы координат к другой, полученной в результате поворота осей координат и переноса начала координат, то есть являются инвариантамикривой Г относительно поворота осей координат и переноса начала.



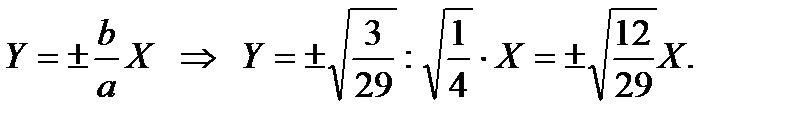
 (3.1)
(3.1) отличен от нуля.
отличен от нуля. — эллипсоид,
— эллипсоид, — мнимый эллипсоид,
— мнимый эллипсоид, — однополостный гиперболоид,
— однополостный гиперболоид, — двуполостный гиперболоид,
— двуполостный гиперболоид, — конус,
— конус,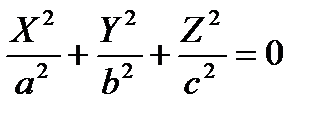 — мнимый конус (точка),
— мнимый конус (точка), — эллиптический параболоид,
— эллиптический параболоид, — гиперболический параболоид,
— гиперболический параболоид, — эллиптический цилиндр,
— эллиптический цилиндр, — мнимый эллиптический цилиндр,
— мнимый эллиптический цилиндр,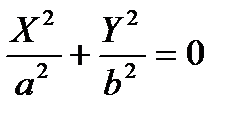 — две мнимые пересекающиеся плоскости (ось O ' Z),
— две мнимые пересекающиеся плоскости (ось O ' Z), — гиперболический цилиндр,
— гиперболический цилиндр, — две пересекающиеся плоскости,
— две пересекающиеся плоскости,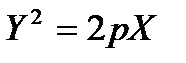 — параболический цилиндр,
— параболический цилиндр, — две параллельные плоскости,
— две параллельные плоскости, — две мнимые параллельные плоскости,
— две мнимые параллельные плоскости, — две совпадающие плоскости (плоскость XOZ).
— две совпадающие плоскости (плоскость XOZ).


