
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полная механическая энергия частицы.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Известно, что приращение кинетической энергии частицы при перемещении в силовом поле равно элементарной работе всех сил, действующих на частицу: Работа всех этих сил идет на изменение кинетической энергии частицы:
Известно также, что работу консервативных сил поля можно записать как убыль потенциальной энергии частицы в этом поле.
Т.о. работа сторонних сил идёт на приращение величины Отсюда видно, что
т.е., приращение полной механической энергии частицы на некотором пути равно работе сторонних сил, действующих на частицу на этом пути; Если Пример: Для тела, падающего с обрыва, работа сторонних сил:
Закон сохранения механической энергии частицы. Из выражения Если сторонние силы отсутствуют, то полная механическая энергия частицы в стационарном поле консервативных сил остается постоянной.
Закон сохранения позволяет решать многие задачи, не привлекая уравнения движения, которые часто приводят к громоздким расчетам.
Кинематика и динамика вращательного движения. Кинематика.
Для истинных векторов типа
 называется угловой скоростью тела, она направлена вдоль оси вращения, в сторону, определяемую правилом правого винта, называется угловой скоростью тела, она направлена вдоль оси вращения, в сторону, определяемую правилом правого винта,  также псевдовектор, модуль угловой скорости равен также псевдовектор, модуль угловой скорости равен  . Если . Если  , то наблюдается равномерное вращение , то наблюдается равномерное вращение  , для равномерного движения , для равномерного движения  есть угол поворота в единицу времени. Для такого движения можно ввести период вращения есть угол поворота в единицу времени. Для такого движения можно ввести период вращения  и частоту: число оборотов за 1 с. и частоту: число оборотов за 1 с.  , а , а  . .
Вектор
Если ось вращения не изменяет своего положения в пространстве, то векторы Точки вращающегося тела имеют разные линейные скорости, которые определяются угловой скоростью Найдем связь между векторами Таким образом: Модуль нормального ускорения точек
Когда ось вращения не поворачивается в пространстве, тангенциальное ускорение можно представить:
Таким образом, нормальное и тангенциальное ускорения растут пропорционально радиусу точек.
|
||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 949; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.152.146 (0.008 с.) |

 . Если частица находится в стационарном поле консервативных сил, то на нее кроме консервативной силы
. Если частица находится в стационарном поле консервативных сил, то на нее кроме консервативной силы  могут действовать и другие силы, называемые сторонними
могут действовать и другие силы, называемые сторонними  ; Тогда результирующая сила равна:
; Тогда результирующая сила равна:  .
.
 , значит
, значит  или
или
 . Эту величину называют полной механической энергией частицы в поле:
. Эту величину называют полной механической энергией частицы в поле:  .
. определяется с точностью до постоянной, так как с точностью до постоянной
определяется с точностью до постоянной, так как с точностью до постоянной  определяется
определяется  . Теперь можно записать
. Теперь можно записать (***)
(***) , то полная механическая энергия частицы растёт. При
, то полная механическая энергия частицы растёт. При  — уменьшается.
— уменьшается. , где
, где  - силы сопротивления.
- силы сопротивления. следует, что в стационарном поле консервативных сил полная механическая энергия частицы может изменяться только под действием сторонних сил, отсюда вытекает закон сохранения механической энергии частицы:
следует, что в стационарном поле консервативных сил полная механическая энергия частицы может изменяться только под действием сторонних сил, отсюда вытекает закон сохранения механической энергии частицы: ;
; 
 Поворот тела на некоторый угол
Поворот тела на некоторый угол  можно задать в виде отрезка, длина которого
можно задать в виде отрезка, длина которого  При поворотах на очень малые углы, путь проходимый точкой можно считать прямолинейным, поэтому два последовательных малых поворота
При поворотах на очень малые углы, путь проходимый точкой можно считать прямолинейным, поэтому два последовательных малых поворота  и
и  (вокруг разных осей; в данном случае оси перпендикулярны) обуславливают, как видно из рис., такое же перемещение,
(вокруг разных осей; в данном случае оси перпендикулярны) обуславливают, как видно из рис., такое же перемещение,  любой точки тела, как и поворот
любой точки тела, как и поворот  получаемый из
получаемый из  связывается с направлением вращения тела, следовательно
связывается с направлением вращения тела, следовательно  вопрос об их направлении не возникает, он решается естественным образом, из природы самих физических величин. Векторы типа
вопрос об их направлении не возникает, он решается естественным образом, из природы самих физических величин. Векторы типа  , направление которых определяется направлением вращения, называются псевдовекторами или аксиальными векторами.
, направление которых определяется направлением вращения, называются псевдовекторами или аксиальными векторами.
 Понятия
Понятия  и
и  можно сохранить и для неравномерного вращения, понимая под ними их мгновенные значения.
можно сохранить и для неравномерного вращения, понимая под ними их мгновенные значения. может изменяться как за счет изменения скорости вращения вокруг оси (по величине), так и за счет поворота оси вращения в пространстве (по направлению). Если за
может изменяться как за счет изменения скорости вращения вокруг оси (по величине), так и за счет поворота оси вращения в пространстве (по направлению). Если за  угловая скорость
угловая скорость  , то изменение угловой скорости со временем характеризуется угловым ускорением:
, то изменение угловой скорости со временем характеризуется угловым ускорением:
 — тоже псевдовектор.
— тоже псевдовектор. коллинеарны.
коллинеарны. . Если за время
. Если за время  , то дуга окружности при этом
, то дуга окружности при этом  . Линейная скорость точки:
. Линейная скорость точки:  ; т.е., связь между модулями скоростей
; т.е., связь между модулями скоростей  .
. и
и  . Из рис. видно, что векторное произведение
. Из рис. видно, что векторное произведение  совпадает с
совпадает с  .
.
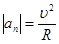 или
или  . Вводя вектор
. Вводя вектор  , перпендикулярный оси вращения, можно записать:
, перпендикулярный оси вращения, можно записать:
 ;
;  -модуль углового ускорения, т.е.,
-модуль углового ускорения, т.е.,  .
.


