
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ускорение. Нормальное и тангенциальное ускорения.Содержание книги
Поиск на нашем сайте
Движение точки характеризуется также ускорением—быстротой изменения скорости. Если скорость точки за произвольное время
т.е. вектор
Вектор ускорения можно разложить по компонентам: Если траектории точки плоская кривая, то для описания движения можно выбрать два перпендикулярные друг к другу направления: касательной к траектории (орт Поскольку вектор скорости Тогда для ускорения точки можно записать:
Из рис. видно, что
 его можно считать совпадающим с дугой окружности радиуса его можно считать совпадающим с дугой окружности радиуса  с центром в т.0 с центральным углом с центром в т.0 с центральным углом  . .
При перемещении по траектории на длину По направлению
Отсюда видно, что Нормальное ускорение
При ускоренном движении угол
Динамика поступательного движения Поступательное движение Простейшим видом механического движения твердого тела является поступательное движение, при котором прямая, соединяющая любые две точки тела перемещается вместе с телом, оставаясь параллельной| своему первоначальному положению (шарик на пружине относительно Земли, поршень в цилиндре стационарного двигателя, лифт, резец токарного станка и др.). Траектории всех точек тела одинаковы. Радиусы - векторы всех точек тела за время
т.е. для описания движения можно взять одну точку тела; если при этом
Закон инерции. В основе классической механики лежат три закона Ньютона, сформулированные им в сочинении «Математические начала натуральной философии», опубликованном в 1687г. Эти законы явились результатом гениального обобщения опытных данных и теоретических закономерностей в области механики, которые были установлены Ньютоном, а также Кеплером. Галилеем, Гюйгенсом. Гуком и др. В качестве первого закона динамики Ньютон принял закон, установленный еще Галилеем: Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока внешнее воздействие не заставит изменить это состояние. Этот закон утверждает, что для состояния покоя или равномерного прямолинейного движения не требуется внешних воздействий. В этом проявляется особое динамическое свойство тел, называемое инертностью. Поэтому первый закон Ньютона называют также законом инерции, а движение тела в отсутствии внешних воздействий, движением по инерции. В этой формулировке закона считается, что тело не деформируется, т.е. оно абсолютно твердое, и что оно движется поступательно. Однако, твердое тело может еще равномерно вращаться по инерции, обладая при этом ускорением. Необходимость во всех этих оговорках отпадает, если в первом законе Ньютона говорить не о теле, а о материальной точке, которая по определению не может ни деформироваться, ни вращаться. Поэтому для материальной точки пользуются формулировкой: материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока внешнее воздействие не выведет её из этого состояния.
|
||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 639; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.150.40 (0.01 с.) |

 изменяется на величину
изменяется на величину  , то величина
, то величина называется средним ускорением точки за это время. Ускорение в данный момент времени:
называется средним ускорением точки за это время. Ускорение в данный момент времени: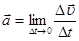 ;
; 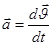
 равен производной
равен производной  по времени. Направление вектора
по времени. Направление вектора  совпадает с направлением приращения скорости
совпадает с направлением приращения скорости 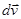 за
за  . Поскольку,
. Поскольку, 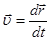 , то ускорение точки можно записать как вторую производную по времени от радиуса-вектора:
, то ускорение точки можно записать как вторую производную по времени от радиуса-вектора: ;
; ; где
; где 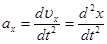 , соответственно,
, соответственно,  …проекции ускорения на оси координат.
…проекции ускорения на оси координат.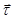 ) и нормали к ней (орт
) и нормали к ней (орт  ). Тогда
). Тогда  .
. , получим для скорости:
, получим для скорости:  .
. ;
; есть разность векторов
есть разность векторов  и
и  есть приращение орта касательной к траектории, соответствующее элементарному пути
есть приращение орта касательной к траектории, соответствующее элементарному пути 
 за время
за время 
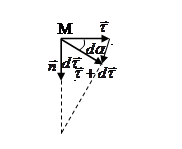
 . Из равнобедренного треугольника векторов
. Из равнобедренного треугольника векторов  , ввиду малости
, ввиду малости  совпадает с ортом
совпадает с ортом  вектор
вектор 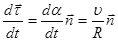 и полное ускорение точки
и полное ускорение точки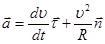 ;
; — касательное (тангенциальное) ускорение характеризует быстроту изменения модуля скорости. При ускоренном движении
— касательное (тангенциальное) ускорение характеризует быстроту изменения модуля скорости. При ускоренном движении  и
и  совпадает с
совпадает с  и
и  характеризует быстроту изменения направления вектора скорости. Оно направлено к центру кривизны траектории;
характеризует быстроту изменения направления вектора скорости. Оно направлено к центру кривизны траектории; 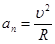 ; поэтому его также называют центростремительным. При прямолинейном движении
; поэтому его также называют центростремительным. При прямолинейном движении  .
. Модуль полного ускорения
Модуль полного ускорения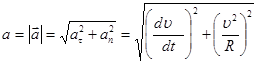 ;
; острый, рис., при замедленном - тупой (
острый, рис., при замедленном - тупой ( , то
, то  и
и  , т.е. перпендикулярно касательной к траектории.
, т.е. перпендикулярно касательной к траектории. , скорости всех точек и их ускорения одинаковы:
, скорости всех точек и их ускорения одинаковы: ;
; 
 , то
, то  и тогда, интегрируя, находим скорость точки:
и тогда, интегрируя, находим скорость точки: ; Затем, интегрируя скорость
; Затем, интегрируя скорость  , найдем координату:
, найдем координату:



