
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 3. Динамика материальной точки и механической системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Опорный конспект лекций
Часть 2
РАЗДЕЛ 3. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ Динамика материальной точки 3.1.1.Основное уравнение динамики материальной точки в случае, когда на точку действуют n сил, имеет вид: Основное уравнение динамики несвободной точки удобно представить в следующей форме:
где Реакции связей, при необходимости, могут быть исключены из уравнений движения, или найдены с помощью специальных приемов. 3.1.2. Сила инерции. Уравнение кинетостатики материальной точки. Уравнение динамики относительного движения Сила инерции по Даламберу: Основное уравнение динамики точки благодаря введению силы инерции преобразуется в уравнение кинетостатики:
Основное уравнение динамики относительного движения точки:
где 3.1.3. Две задачи динамики материальной точки Первая (прямая) задача: определение неизвестных величин (например, реакций связей) по заданным кинематическим параметрам движения точки. Вторая (обратная) задача: определение движения точки по заданным силам, связям и начальным условиям. 3.1.4.Решение обратной задачи динамики свободной материальной точки обычно включает в себя следующие этапы: - составление системы дифференциальных уравнений движения точки и начальных условий к ним (формализация задачи: создание математической модели); - решение задачи Коши: построение частного решения системы при заданных начальных условиях (работа с формализованной моделью); - кинематические исследования (интерпретация формальных результатов). Примем условие, согласно которому задаваемые силы могут зависеть от времени, положения точки и от скорости точки (но не зависят от ускорения и производных от него). Дифференциальные уравнения движения свободной точки в пространстве в декартовой системе координат могут иметь вид:
Это система дифференциальных уравнений второго порядка относительно неизвестных функций Процесс отыскания решения называется интегрированием системы дифференциальных уравнений. В этом процессе применяются различные приемы: понижение порядка уравнения, разделение переменных и т.д. Совокупность функций 3.1.5. Начальные условия (НУ) при решении обратной задачи динамики точки – это условия, накладываемые на начальную скорость и начальное положение точки, записанные, например следующим образом:
Число начальных условий должно соответствовать числу и порядку дифференциальных уравнений движения (условию корректности постановки задачи Коши). НУ должны быть сформулированы в терминах тех неизвестных функций, которые участвуют в записях дифференциальных уравнений. 3.1.6. Некоторые простейшие задачи динамики материальной точки, решаемые методами понижения порядка и разделения переменных. Пусть свободная материальная точка движется по прямой 1) Рассмотрим случай, когда сила является функцией времени (или постоянна):
Представив
2) Сила является функцией проекции скорости
а) Пусть требуется определить зависимость между проекцией скорости
Данная запись имеет смысл при условии б) Пусть требуется найти зависимость между величинами
3) Сила является функцией положения точки. После замены переменной имеем: Пример. Некоторое тело, имея отрицательную плавучесть величиной
а б в Рис. 1. Задача о погружении тела
Объектом исследования является погружающееся тело, принимаемое за материальную точку. Глубину погружения будем считать малой в сравнении с радиусом Земли, а время погружения ограничивать не будем:
Введем ось
Подставив заданное выражение для силы сопротивления
с начальным условием (НУ) В начале движения
Поскольку
из НУ следует, что
Выражение Если тело попадает в воду с начальной скоростью
3.1.7. К задачеоб исследовании движения тела, брошенного под углом При скорости 1) инерциальная система отсчета – геоцентрическая; 2) ускорение свободного падения 3) кривизна поверхности Земли не учитывается; 4) влияние воздуха на движение тела не учитывается. Тогда, в результате интегрирования дифференциальных уравнений движения, получаем кинематические уравнения движения в системе координат
Дальность обстрела, определяемая выражением При скоростях
где
Число Рейнольдса определяется по формуле При скоростях При стрельбе под большим углом возвышения При расчетах учитывалась зависимость плотности воздуха и ускорения свободного падения от высоты, геофизические данные о местности, включая кривизну земной поверхности, а также метеорологические данные о скорости и направлении ветра, давлении воздуха и проч. Из 303 снарядов 120 упало за пределами Парижа. Уже к началу 1-й Мировой войны таблицы ответственных стрельб составлялись по отношению к гелиоцентрической системе отсчета. Так, в начале боя между немецкой и английской эскадрами у Фолклендских островов в 1914 г. английские снаряды упорно ложились на 100 м левее цели. Командование забыло перевести поправку на вращение Земли, рассчитанную для 3.1.8. Свободные гармонические незатухающие колебания материальной точки Условием колебательного движения является наличие восстанавливающей силы, «стремящейся» вернуть материальную точку в положение равновесия, в котором величина восстанавливающей силы равна нулю. Простейшая модель колебательной системы – прямолинейное движение точечной массы под действием упругой силы, подчиняющейся закону Гука (рис. 2,а):
где
а б Рис. 2. Динамическая модель гармонического осциллятора
При
Колебания, описываемые данным уравнением, происходят благодаря действию только восстанавливающей силы и называются свободными. Величина Период колебаний определяется формулой Общее решение дифференциального уравнения гармонического осциллятора имеет вид График функции Амплитуда Фазой называется значение аргумента 3.1.9. Эквивалентная жесткость системы двух упругих элементов при параллельном их соединении равна
Эквивалентная податливость (величина, обратная жесткости) при последовательном соединении двух упругих элементов равна
3.1.10. Свободные затухающие колебания материальной точки возникают при наличии (помимо восстанавливающей силы) силы сопротивления; на наличие этой силы указывают, изображая на рисунке с гармоническим осциллятором демпфирующий элемент (рис. 2,б) в виде цилиндра с поршнем (Der Dämpfer (нем.) - «успокоитель»). Сила сопротивления В случае, когда величина этой силы пропорциональна скорости (
где обозначено Характеристическое уравнение Если
где Амплитуды составляют бесконечно убывающую геометрическую прогрессию, знаменатель 3.1.11. Фазовый «портрет» гармонического осциллятора Введя переменную
Переменные Фазовые траектории гармонического осциллятора без сопротивления - эллипсы; начало координат О – точка равновесия - является особой точкой типа «центр» для описанной выше системы двух уравнений. Центр О является устойчивой особой точкой: изображающая точка не отклонится от центра больше, чем на расстояние, задаваемое начальным (и остающимся постоянным) значением полной энергии осциллятора. Фазовые траектории осциллятора с сопротивлением, пропорциональным скорости, представляют собой спирали, приближающиеся асимптотически к точке О, при этом радиус-вектор изображающей точки бесконечно много раз поворачивается вокруг точки О. Точка О представляет собой асимптотически устойчивый фокус. На рис. 3 изображены фазовые траектории колебаний, происходящих по закону
Рис. 3. Фазовый портрет осциллятора с демпфером
В случае большого сопротивления ( 3.1.12. Вынужденные колебаниягармонического осциллятора под действием гармонической вынуждающей силы Пусть проекция вынуждающей силы есть
Решение дифференциального уравнения вынужденных колебаний, удовлетворяющее начальным условиям
где функции
при этом *3.1.13. Вынужденные колебания вблизи резонанса и при резонансе Пусть частота вынуждающей силы, возрастая, приближается к значению собственной частоты, так что
Известные формулы разложения тригонометрических функций в степенные ряды в окрестности нулевого значения аргумента
убеждают нас, что при малом значении Используя приведенные выше разложения и обозначая через
а б в Рис. 4. Биения. Вековой член функции
где На рис. 4,б график «векового» (secular) члена 3.1.14. Коэффициент динамичности. АЧХ (амплитудно-частотная характеристика) гармонического осциллятора Коэффициентом динамичности
где *3.1.15. Действие произвольнойпериодической силы на гармонический осциллятор Пусть на осциллятор действует некоторая периодическая сила периода
можно представить в виде ряда Фурье
где *3.1.16. Действие произвольной вынуждающей силы на гармонический осциллятор Пусть в дифференциальном уравнении вынужденных колебаний гармонического осциллятора
Приведенный здесь интеграл называется свёрткой функций
Решение уравнения вынужденных колебаний можно построить операционным методом, переходя от исходных функций времени (оригиналов) к их изображениям (функциям комплексного переменного
Изображение свертки двух функций есть произведение их изображений:
*3.1.17. Гармонический осциллятор как звено САУ (системы автоматического управления). Передаточная функция звена. Построим изображения по Лапласу левой и правой частей уравнения вынужденных колебаний осциллятора (п. 3.1.15) при нулевых начальных условиях (!):
откуда получаем формальное выражение
Это выражение описывает соотношение между сигналом
называется передаточной функцией колебательного звена САУ. Блок-схема САУ изображает ее структуру; передаточные функции звеньев характеризуют преобразование этими звеньями входных сигналов в выходные. В приведенном на рис. 5 фрагменте блок-схемы звено 2 является сумматором с отрицательной обратной связью. Сигнал, подаваемый на затемненный сектор, инвертируется, т.е. подается на вход сумматора с противоположным знаком. Звено 4 является, судя по передаточной функции, колебательным звеном с сопротивлением.
Рис. 5. Фрагмент блок-схемы САУ
*3.1.18. Вынужденные колебания гармонического осциллятора с сопротивлением Пусть дифференциальное уравнение движения осциллятора имеет вид:
Частное решение этого уравнения, ввиду присутствия члена
где Коэффициент динамичности где, в дополнение к п. 3.1.14, обозначено Исследуем возможность наличия экстремума этой функции:
Отсюда получаем
Рис. 6. АЧХ осциллятора с демпфером
Кривая, соответствующая значению
3.1.19. Примерыколебательного движения а) Пусть в начальный момент времени заряд
а б в г Рис. 7. Устройства, демонстрирующие колебательное движение
Как известно из курса общей физики,
где б) Вертикальные колебания цилиндрического поплавка (рис. 7,б) длиной
где | ||
|
| Поделиться: |

 .
.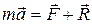 ,
, - равнодействующая задаваемых сил, приложенных к точке,
- равнодействующая задаваемых сил, приложенных к точке, 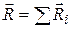 - равнодействующая реакций связей.
- равнодействующая реакций связей.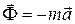 - «фиктивная» сила, приложенная к материальной точке. Определенного контрагента в данном взаимодействии нет. В роли контрагента здесь выступает универсум - весь мир, окружающий данную материальную точку.
- «фиктивная» сила, приложенная к материальной точке. Определенного контрагента в данном взаимодействии нет. В роли контрагента здесь выступает универсум - весь мир, окружающий данную материальную точку. .
.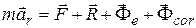 ,
,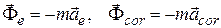 - переносная и кориолисова силы инерции. Это уравнение описывает движение точки относительно неинерциальной системы отсчета, совершающей движение относительно инерциальной системы.
- переносная и кориолисова силы инерции. Это уравнение описывает движение точки относительно неинерциальной системы отсчета, совершающей движение относительно инерциальной системы.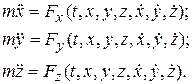
 . Решить систему означает найти такие функции
. Решить систему означает найти такие функции 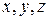 , которые при подстановке в уравнения системы обращают их в тождества, справедливые при любом значении независимой переменной
, которые при подстановке в уравнения системы обращают их в тождества, справедливые при любом значении независимой переменной  из промежутка [0;T], на котором исследуется движение (правая граница может быть бесконечностью).
из промежутка [0;T], на котором исследуется движение (правая граница может быть бесконечностью). . Постоянные интегрирования определяются в результате решения системы уравнений, получающейся в результате совмещении общего решения с начальными условиями.
. Постоянные интегрирования определяются в результате решения системы уравнений, получающейся в результате совмещении общего решения с начальными условиями.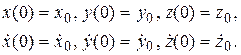
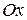 под действием задаваемой силы, проекция которой на ось
под действием задаваемой силы, проекция которой на ось  . Обозначив
. Обозначив 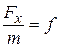 , запишем дифференциальное уравнение движения в проекциях на ось
, запишем дифференциальное уравнение движения в проекциях на ось  .
.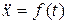 .
.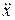 как
как 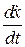 , понижаем порядок уравнения, а затем, умножив обе части на
, понижаем порядок уравнения, а затем, умножив обе части на  , разделяем переменные:
, разделяем переменные: .
. :
: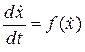 .
. и временем. Умножая обе части уравнения на величину
и временем. Умножая обе части уравнения на величину  , разделяем переменные:
, разделяем переменные: .
. (т.е. должно быть
(т.е. должно быть  или
или 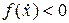 ).
).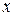 и
и  и получаем:
и получаем: (
(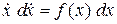 . Решение этого уравнения называют интегралом энергии.
. Решение этого уравнения называют интегралом энергии.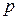 , погружается в воду из состояния покоя (рис. 1, а). Сила сопротивления воды равна
, погружается в воду из состояния покоя (рис. 1, а). Сила сопротивления воды равна 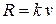 , где
, где 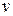 - скорость погружения,
- скорость погружения, 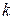 - постоянный коэффициент. Масса тела
- постоянный коэффициент. Масса тела  . Определить скорость погружения тела. (Плавучестью называется разность между силой Архимеда
. Определить скорость погружения тела. (Плавучестью называется разность между силой Архимеда 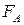 и силой тяжести. Если плавучесть положительна, то тело всплывает. Здесь
и силой тяжести. Если плавучесть положительна, то тело всплывает. Здесь 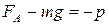 .)
.)
 . Изображаем в произвольный момент времени
. Изображаем в произвольный момент времени 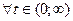 тело (рис. 1,а) и действующие на него силы. Записываем основное уравнение динамики точки в векторной форме:
тело (рис. 1,а) и действующие на него силы. Записываем основное уравнение динамики точки в векторной форме: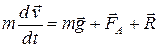 .
.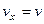 . Запишем уравнение движения (2) в проекциях на ось
. Запишем уравнение движения (2) в проекциях на ось 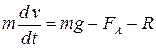 .
.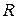 , получаем дифференциальное уравнение относительно неизвестной функции
, получаем дифференциальное уравнение относительно неизвестной функции  :
: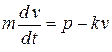
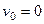 .
.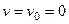 и выражение
и выражение  . Пусть последнее неравенство выполняется во все время движения. Разделяем переменные; преобразуем; интегрируем:
. Пусть последнее неравенство выполняется во все время движения. Разделяем переменные; преобразуем; интегрируем: ;
;  ;
;  .
. . Из формулы для силы
. Из формулы для силы  следует, что размерность коэффициента
следует, что размерность коэффициента  есть
есть 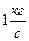 , и тогда размерность
, и тогда размерность  . Обозначим
. Обозначим 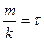 - это так называемая постоянная времени релаксации. Находим далее:
- это так называемая постоянная времени релаксации. Находим далее: или
или 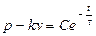 ;
;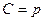 , и тогда получаем
, и тогда получаем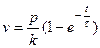 .
. , имеющее размерность скорости и равное пределу
, имеющее размерность скорости и равное пределу  обозначим как
обозначим как  . График функции
. График функции 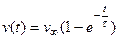 имеет горизонтальную асимптоту
имеет горизонтальную асимптоту 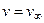 (рис. 1,б). Величина
(рис. 1,б). Величина  наличия экстремума; только здесь экстремум достигается в несобственной точке
наличия экстремума; только здесь экстремум достигается в несобственной точке  , то график скорости имеет вид, приведенный на рис. 1, в. «Сверхпредельное» движение не может само собой перейти в «допредельное» и наоборот.
, то график скорости имеет вид, приведенный на рис. 1, в. «Сверхпредельное» движение не может само собой перейти в «допредельное» и наоборот. к горизонту с начальной скоростью
к горизонту с начальной скоростью 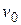 .
. рассматривают простейшую модель задачи, удовлетворяющую условиям:
рассматривают простейшую модель задачи, удовлетворяющую условиям: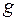 постоянно;
постоянно; (ось
(ось  направлена вверх):
направлена вверх): .
.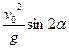 , достигает максимального значения при
, достигает максимального значения при  . Пуля, выпущенная из винтовки Мосина обр.1891г. с начальной скоростью 620 м/с, имела бы при выполнении сформулированных условий максимальную дальность полета около 40 км (в действительности, из-за сопротивления воздуха, менее 4 км).
. Пуля, выпущенная из винтовки Мосина обр.1891г. с начальной скоростью 620 м/с, имела бы при выполнении сформулированных условий максимальную дальность полета около 40 км (в действительности, из-за сопротивления воздуха, менее 4 км).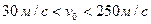 условие 4 преобразуется: вводится сила сопротивления воздуха
условие 4 преобразуется: вводится сила сопротивления воздуха 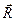 , зависящая от скорости
, зависящая от скорости  тела согласно формуле
тела согласно формуле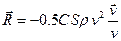 ,
, - площадь поперечного сечения тела,
- площадь поперечного сечения тела,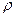 - плотность воздуха (
- плотность воздуха (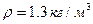 при нормальных условиях),
при нормальных условиях), - коэффициент лобового сопротивления, зависящий от формы тела и от числа Рейнольдса
- коэффициент лобового сопротивления, зависящий от формы тела и от числа Рейнольдса 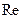 , характеризующего процесс обтекания тела воздухом.
, характеризующего процесс обтекания тела воздухом. . В этой формуле
. В этой формуле 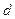 означает «характерный размер» тела (напр., диаметр пушечного ядра),
означает «характерный размер» тела (напр., диаметр пушечного ядра), 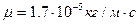 - вязкость воздуха. Для пушечного ядра
- вязкость воздуха. Для пушечного ядра  во время движения и, следовательно, сила сопротивления пропорциональна квадрату скорости ядра.
во время движения и, следовательно, сила сопротивления пропорциональна квадрату скорости ядра. приходится пересматривать все условия первоначальной модели. При сверхзвуковых скоростях снарядов нарезного оружия сила лобового сопротивления характеризуется волновым сопротивлением: около снаряда образуется волна сильного сжатия, которая расходится от него в виде конуса. Этот конус называется конусом Маха и имеет угол раствора
приходится пересматривать все условия первоначальной модели. При сверхзвуковых скоростях снарядов нарезного оружия сила лобового сопротивления характеризуется волновым сопротивлением: около снаряда образуется волна сильного сжатия, которая расходится от него в виде конуса. Этот конус называется конусом Маха и имеет угол раствора  (
(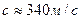 - скорость звука). Коэффициент С при сверхзвуковой скорости движения
- скорость звука). Коэффициент С при сверхзвуковой скорости движения 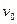 порядка
порядка  и более, значительная часть траектории снаряда пролегает на высоте свыше 20 км, где сопротивление воздуха незначительно. В 1918г. германская артиллерия из орудий «Колоссаль» обстреливала Париж с расстояния 115 км. Стрельба велась при угле
и более, значительная часть траектории снаряда пролегает на высоте свыше 20 км, где сопротивление воздуха незначительно. В 1918г. германская артиллерия из орудий «Колоссаль» обстреливала Париж с расстояния 115 км. Стрельба велась при угле  с начальной скоростью 2000 м/с. Наивысшая точка траектории лежала на высоте 40 км, время полета снаряда 3.5 мин (из них 2 мин в стратосфере). Калибр 210 мм, вес снаряда 120 кг, длина ствола 34 м, вес орудия 750 тонн. Заряд составлял около 200 кг пороха и развивал давление в канале ствола 5000 атм.
с начальной скоростью 2000 м/с. Наивысшая точка траектории лежала на высоте 40 км, время полета снаряда 3.5 мин (из них 2 мин в стратосфере). Калибр 210 мм, вес снаряда 120 кг, длина ствола 34 м, вес орудия 750 тонн. Заряд составлял около 200 кг пороха и развивал давление в канале ствола 5000 атм. северной широты (в северном полушарии летящие по пологой траектории снаряды отклоняются вправо благодаря Кориолисовой силе инерции), на южную широту
северной широты (в северном полушарии летящие по пологой траектории снаряды отклоняются вправо благодаря Кориолисовой силе инерции), на южную широту  .
.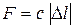 ,
, - коэффициент упругости (жесткость) пружины,
- коэффициент упругости (жесткость) пружины,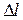 - деформация упругого элемента (пружины):
- деформация упругого элемента (пружины):  ,
, - длина пружины в рассматриваемый момент времени,
- длина пружины в рассматриваемый момент времени,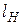 - длина недеформированной пружины.
- длина недеформированной пружины.
 тело массой
тело массой 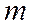 находится в положении равновесия. Взяв начало координат
находится в положении равновесия. Взяв начало координат  в положении равновесия тела и направив ось
в положении равновесия тела и направив ось 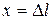 и
и  ), получаем дифференциальное уравнение движения тела - дифференциальное уравнение гармонического (линейного) осциллятора (устройства, совершающего колебательное движение)
), получаем дифференциальное уравнение движения тела - дифференциальное уравнение гармонического (линейного) осциллятора (устройства, совершающего колебательное движение)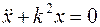 .
. называется циклической частотой колебаний и измеряется в радианах в секунду (в отличие от частоты, измеряемой в Герцах). Циклическая частота свободных колебаний называется собственной частотой колебательного устройства (осциллятора).
называется циклической частотой колебаний и измеряется в радианах в секунду (в отличие от частоты, измеряемой в Герцах). Циклическая частота свободных колебаний называется собственной частотой колебательного устройства (осциллятора).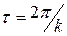 .
.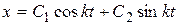 , а частное решение, удовлетворяющее начальным условиям
, а частное решение, удовлетворяющее начальным условиям 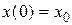 ,
,  , можно представить как
, можно представить как 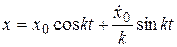 , или
, или  .
. имеет вид синусоиды, и такие колебания называются гармоническими.
имеет вид синусоиды, и такие колебания называются гармоническими. и начальный сдвиг
и начальный сдвиг 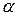 фазы колебаний находятся из выражений
фазы колебаний находятся из выражений 
 в данный момент времени. Функция
в данный момент времени. Функция  задается тремя параметрами:
задается тремя параметрами:  , характеризующими амплитуду, частоту и фазу колебаний. С помощью колебательного процесса передают информацию путем амплитудной, частотной или фазовой модуляции.
, характеризующими амплитуду, частоту и фазу колебаний. С помощью колебательного процесса передают информацию путем амплитудной, частотной или фазовой модуляции.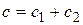 .
.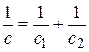 .
.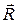 - следящая сила, направленная всегда против вектора скорости:
- следящая сила, направленная всегда против вектора скорости: 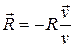 .
.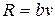 ), а движение прямолинейно, проекция силы
), а движение прямолинейно, проекция силы 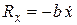 , и дифференциальное уравнение движения тела приобретает вид
, и дифференциальное уравнение движения тела приобретает вид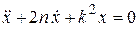 ,
,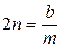 .
. , рассмотренное как приведенное квадратное уравнение, имеет дискриминант
, рассмотренное как приведенное квадратное уравнение, имеет дискриминант  . Если
. Если 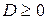 , то движение тела носит апериодический характер («чистое затухание»).
, то движение тела носит апериодический характер («чистое затухание»).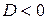 (случай малого сопротивления), то тело совершает свободные затухающие колебания. Общее решение уравнения движения может быть представлено в виде
(случай малого сопротивления), то тело совершает свободные затухающие колебания. Общее решение уравнения движения может быть представлено в виде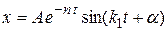 ,
, .
.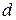 которой называется декрементом затухания (характеристика роста называлась бы инкрементом). Величина
которой называется декрементом затухания (характеристика роста называлась бы инкрементом). Величина 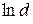 называется логарифмическим декрементом затухания.
называется логарифмическим декрементом затухания. , можно для гармонического осциллятора вместо одного дифференциального уравнения второго порядка записать систему двух уравнений первого порядка:
, можно для гармонического осциллятора вместо одного дифференциального уравнения второго порядка записать систему двух уравнений первого порядка: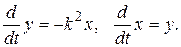
 , удовлетворяющие этой системе, называются фазовыми переменными; плоскость
, удовлетворяющие этой системе, называются фазовыми переменными; плоскость  называют фазовой плоскостью; точку с координатами
называют фазовой плоскостью; точку с координатами  - изображающей точкой. Траектория изображающей точки – фазовая траектория. Множество фазовых траекторий, исходящих из разных начальных точек, представляет фазовый «портрет» процесса, описываемого данной системой дифференциальных уравнений. Движение изображающей точки по фазовой плоскости происходит против часовой стрелки.
- изображающей точкой. Траектория изображающей точки – фазовая траектория. Множество фазовых траекторий, исходящих из разных начальных точек, представляет фазовый «портрет» процесса, описываемого данной системой дифференциальных уравнений. Движение изображающей точки по фазовой плоскости происходит против часовой стрелки.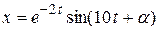 , при трех значениях параметра
, при трех значениях параметра 
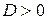 ) фазовые траектории также асимптотически приближаются к точке О, но радиус-вектор изображающей точки, поворачиваясь по часовой стрелке, не совершает ни одного полного оборота.
) фазовые траектории также асимптотически приближаются к точке О, но радиус-вектор изображающей точки, поворачиваясь по часовой стрелке, не совершает ни одного полного оборота.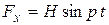 .
.  , запишем дифференциальное уравнение вынужденных колебаний гармонического осциллятора без сопротивления:
, запишем дифференциальное уравнение вынужденных колебаний гармонического осциллятора без сопротивления: .
.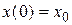 ,
,  , можно записать в виде:
, можно записать в виде: ,
, описывают составляющие колебания осциллятора:
описывают составляющие колебания осциллятора: - свободные колебания,
- свободные колебания,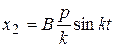 - сопровождающие колебания,
- сопровождающие колебания, - чисто вынужденные колебания,
- чисто вынужденные колебания, . Последнее выражение имеет конечное значение при условии
. Последнее выражение имеет конечное значение при условии 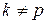 .
.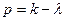 , где
, где  - малая величина. Рассмотрим вынужденные колебания
- малая величина. Рассмотрим вынужденные колебания  :
: .
. ;
;
 при значениях
при значениях  .
. величину высшего порядка малости, чем
величину высшего порядка малости, чем  , получим
, получим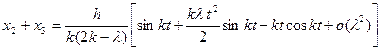 ;
;
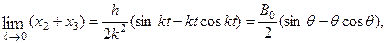
 означает статическую деформацию упругого элемента под действием силы, величиной
означает статическую деформацию упругого элемента под действием силы, величиной  ;
; 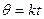 - безразмерное время.
- безразмерное время. , присутствующего в выражении
, присутствующего в выражении  , демонстрирует неограниченный рост амплитуд при продолжении колебаний (при отсутствии сопротивления!).
, демонстрирует неограниченный рост амплитуд при продолжении колебаний (при отсутствии сопротивления!).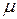 назовем безразмерный коэффициент, выражающий отношение амплитуды
назовем безразмерный коэффициент, выражающий отношение амплитуды  чисто вынужденных колебаний к некоторой характерной (нормирующей) длине, например, к статической деформации
чисто вынужденных колебаний к некоторой характерной (нормирующей) длине, например, к статической деформации  :
: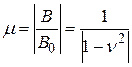 ,
,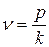 означает безразмерную частоту. График этой функции (рис. 4,в) изображает АЧХ гармонического осциллятора. Правая часть графика убеждает нас в том, что когда частота вынуждающей силы значительно превосходит собственную частоту осциллятора, вынужденные колебания весьма малы.
означает безразмерную частоту. График этой функции (рис. 4,в) изображает АЧХ гармонического осциллятора. Правая часть графика убеждает нас в том, что когда частота вынуждающей силы значительно превосходит собственную частоту осциллятора, вынужденные колебания весьма малы. . Тогда правую часть дифференциального уравнения его движения
. Тогда правую часть дифференциального уравнения его движения
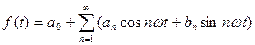 ,
, . В силу линейности дифференциального уравнения движения частное его решение представляет собой аналогичный ряд. Компоненты этого ряда, характеризующие чисто вынужденные колебания, имеют коэффициенты при функциях
. В силу линейности дифференциального уравнения движения частное его решение представляет собой аналогичный ряд. Компоненты этого ряда, характеризующие чисто вынужденные колебания, имеют коэффициенты при функциях 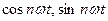 со знаменателями вида
со знаменателями вида  . В случае, когда
. В случае, когда  , имеет место резонанс
, имеет место резонанс  рода.
рода. означает произвольную функцию времени, удовлетворяющую условиям, предъявляемым к оригиналам (см. «Преобразование Лапласа и операционное исчисление» в курсе высшей математики). Тогда частное решение этого уравнения можно представить в виде
означает произвольную функцию времени, удовлетворяющую условиям, предъявляемым к оригиналам (см. «Преобразование Лапласа и операционное исчисление» в курсе высшей математики). Тогда частное решение этого уравнения можно представить в виде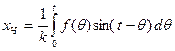 .
.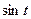 :
: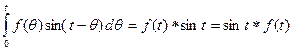 . Выражение
. Выражение  есть функция влияния внешнего воздействия
есть функция влияния внешнего воздействия 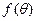 , осуществленного в момент времени
, осуществленного в момент времени 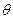 , на положение осциллятора в последующий момент
, на положение осциллятора в последующий момент  .
.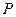 ) согласно формуле
) согласно формуле .
.
 .
.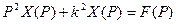 ,
, .
. , подаваемым на вход колебательного звена, и выходным сигналом
, подаваемым на вход колебательного звена, и выходным сигналом  . Выражение
. Выражение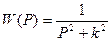

 .
.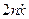 , ищем в виде
, ищем в виде  . Подставив это выражение в уравнение, получим, что чисто вынужденные колебания описываются формулой
. Подставив это выражение в уравнение, получим, что чисто вынужденные колебания описываются формулой
 .
.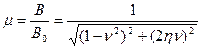 ,
,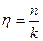 .
.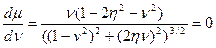 .
.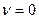 или
или  . Последнее выражение существует при условии
. Последнее выражение существует при условии 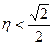 . Амплитудно-частотные характеристики представляют собой зависящее от параметра
. Амплитудно-частотные характеристики представляют собой зависящее от параметра  семейство кривых (рис.6).
семейство кривых (рис.6).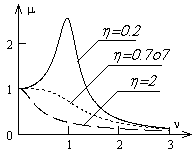
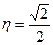 , является сепаратрисой: она разделяет квадрант на две области. Верхняя область соответствует значительной реакции осциллятора на резонансную безразмерную частоту
, является сепаратрисой: она разделяет квадрант на две области. Верхняя область соответствует значительной реакции осциллятора на резонансную безразмерную частоту  емкости (рис. 7,а) равен
емкости (рис. 7,а) равен 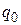 , ключ разомкнут, и электрический ток
, ключ разомкнут, и электрический ток 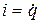 в контуре отсутствует:
в контуре отсутствует: 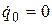 . Ток возникает при замыкании ключа. Для составления уравнения функционирования контура воспользуемся вторым законом Кирхгофа: сумма падений напряжения в замкнутом контуре равна нулю:
. Ток возникает при замыкании ключа. Для составления уравнения функционирования контура воспользуемся вторым законом Кирхгофа: сумма падений напряжения в замкнутом контуре равна нулю: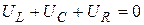 .
.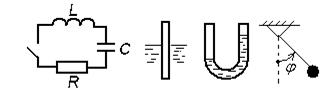
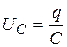 ,
, 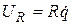 ,
, 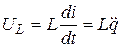 (
( - параметр емкости,
- параметр емкости,  - соленоида,
- соленоида, 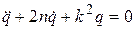 ,
,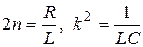 . При малом активном сопротивлении величина заряда, ток и напряжение изменяются согласно закону затухающих колебаний.
. При малом активном сопротивлении величина заряда, ток и напряжение изменяются согласно закону затухающих колебаний. при отсутствии сопротивления жидкости описываются уравнением
при отсутствии сопротивления жидкости описываются уравнением ,
,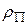 - плотность его материала,
- плотность его материала, 


