
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моменты инерции относительно полюса и относительно плоскостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Эти моменты инерции определяются аналогично осевым моментам формулой
а б в г
Рис. 9. К расчету осевых моментов инерции
Полярный момент инерции относительно начала
Моменты инерции относительно координатных плоскостей
Моменты инерции некоторых однородных тел а) Стержень (прямоугольная пластина) постоянной толщины массой
б) Тонкий обруч (тонкостенная труба) радиуса
в) Сплошной диск (цилиндр) радиуса
Используя формулы п.3.2.8, найдем моменты
В некоторых задачах (например, в статических задачах по сопротивлению материалов) требуется рассчитать момент инерции некоторой фигуры (сечения), плотность которой Потенциальное силовое поле Силовое поле – часть пространства (или все пространство), в каждом пункте которого определена, тем или иным физическим законом, сила, действующая на материальную точку, находящуюся в этом пункте. Силовое поле называется потенциальным (имеющим скалярный потенциал), если существует дважды непрерывно дифференцируемая силовая функция
Тогда работа силы
Работа определяется только начальным и конечным значениями силовой функции и не зависит от формы траектории. Работа на замкнутой траектории (контуре) равна нулю. Выражение для работы вектора силы
Согласно формуле Стокса циркуляция вектора
Потенциальное силовое поле, задаваемое скалярным потенциалом Ротор (вихрь, он же
Поверхности вида Потенциальная энергия Потенциальная энергия Выберем одну из поверхностей уровня и назначим ее поверхностью нулевого уровня потенциальной энергии, т.е. на этой поверхности считается Потенциальная энергия малого фрагмента системы, находящегося в точке
Из сравнения с выражением
3.2.12. Работа силы тяжести. Потенциальная энергия тяжелого тела Пусть ось
где Пусть Пример. Пусть м еханическая система (рис. 10,а) состоит из трех тел массами
3.2.13. Работа упругой силы. Потенциальная энергия упругого элемента Пусть упругий элемент механической системы (напр., пружина) деформируется в соответствии с законом Гука (см. п. 3.1.8). Работа упругой силы определяется формулой
где с – коэффициент упругости, Пример. Механическая система (рис. 10,б) состоит из двух тел массами
- квадратичная форма относительно обобщенных координат.
а б в Рис. 10. Механические системы с двумя и с одной степенью свободы
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 639; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.104.23 (0.01 с.) |

 , где
, где  - расстояние от
- расстояние от  - ой точки до полюса или до плоскости.
- ой точки до полюса или до плоскости.
 декартовой системы координат
декартовой системы координат .
. Очевидны соотношения
Очевидны соотношения .
. и длиной
и длиной  (рис. 9,б)
(рис. 9,б) ;
;  .
.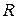 (рис. 9,в)
(рис. 9,в) .
. .
. для сплошного диска (рис. 9, г). Считаем толщину диска малой:
для сплошного диска (рис. 9, г). Считаем толщину диска малой:  , тогда
, тогда .
. условно считается равной единице. Тогда, например, последний момент будет равен
условно считается равной единице. Тогда, например, последний момент будет равен  (масса диска будет равна
(масса диска будет равна  ).
).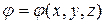 , такая, что в каждой точке поля
, такая, что в каждой точке поля  , где символический вектор-оператор «набла» имеет следующий смысл:
, где символический вектор-оператор «набла» имеет следующий смысл: .
. при перемещении точки приложения силы из пункта 1 в пункт 2 равна (см. ч. 1, п. 2.1.7)
при перемещении точки приложения силы из пункта 1 в пункт 2 равна (см. ч. 1, п. 2.1.7)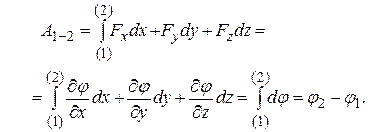
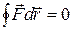 .
. к этой поверхности (ориентированную соответственно направлению обхода контура):
к этой поверхности (ориентированную соответственно направлению обхода контура): .
. , называется также безвихревым, поскольку в нем выполняется условие
, называется также безвихревым, поскольку в нем выполняется условие  (равенство
(равенство  - известное в теории поля тождество).
- известное в теории поля тождество).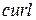 ) вектора
) вектора 
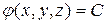 , на которых значение силовой функции постоянно и равно заданной константе С, называются поверхностями уровня, или эквипотенциальными поверхностями.
, на которых значение силовой функции постоянно и равно заданной константе С, называются поверхностями уровня, или эквипотенциальными поверхностями. тела (и механической системы вообще) складывается из потенциальных энергий отдельных его фрагментов.
тела (и механической системы вообще) складывается из потенциальных энергий отдельных его фрагментов. .
.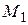 поля, равна работе, совершаемой силой
поля, равна работе, совершаемой силой  . Тогда
. Тогда
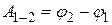 следует, что
следует, что ;
;  .
. направлена вертикально вверх. Работа постоянной силы
направлена вертикально вверх. Работа постоянной силы  , приложенной в центре тяжести тела, равна
, приложенной в центре тяжести тела, равна , или
, или  ,
, - перепад высот между начальным и конечным положениями центра тяжести тела - малая величина сравнительно с радиусом Земли. Из формулы следует, что работа не зависит от формы траектории центра тяжести, следовательно, гравитационное поле потенциально. Потенциальная энергия тела зависит от положения его центра тяжести:
- перепад высот между начальным и конечным положениями центра тяжести тела - малая величина сравнительно с радиусом Земли. Из формулы следует, что работа не зависит от формы траектории центра тяжести, следовательно, гравитационное поле потенциально. Потенциальная энергия тела зависит от положения его центра тяжести:  . Пусть
. Пусть  ; тогда
; тогда  .
. , где
, где  - гравитационная постоянная, М – масса Земли,
- гравитационная постоянная, М – масса Земли, 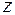 - расстояние от центра Земли до центра тяжести тела. Пусть
- расстояние от центра Земли до центра тяжести тела. Пусть  ; тогда
; тогда  .
. , невесомых нерастяжимых нитей и невесомых блоков. Она имеет 2 степени свободы; назначаем обобщенные координаты
, невесомых нерастяжимых нитей и невесомых блоков. Она имеет 2 степени свободы; назначаем обобщенные координаты  , отсчитываемые от точек схода нитей. Потенциальная энергия системы есть функция
, отсчитываемые от точек схода нитей. Потенциальная энергия системы есть функция  . Пусть
. Пусть 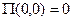 ; тогда
; тогда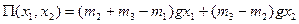 .
.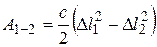 ,
, - начальная деформация,
- начальная деформация,  - конечная деформация пружины. Введем координату
- конечная деформация пружины. Введем координату 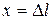 , так что
, так что 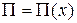 , и пусть
, и пусть  .
. , перемещающихся по горизонтальной направляющей, и невесомых пружин, имеющих упругие параметры
, перемещающихся по горизонтальной направляющей, и невесомых пружин, имеющих упругие параметры 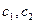 . Назначаем обобщенные координаты
. Назначаем обобщенные координаты  -
-



