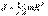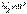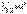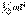Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 9 Работа и кинетическая энергия вращенияСодержание книги
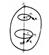
Поиск на нашем сайте Рассмотрим абсолютно твердое тело, вращающееся около неподвижной оси z, проходящей через него (рис. 1.19). Мысленно разобьем это тело на маленькие объемы с элементарными массами т1, т2,..., mn находящиеся на расстоянии r 1, r 2,…, r n от оси.
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов: Отсюда, получаем где J z – момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела
Учитывая, что масса в классической механике есть величина постоянная, в выражении (1.9) ее можно внести под знак производной:
Векторная величина Подставляя (1.11) в (1.10), получим
Это выражение – называется уравнением движения материальной точки – более общая формулировка второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе. Единица силы в СИ – ньютон (Н): 1 Н – сила, которая массе 1 кг сообщает ускорение 1 м/с2 в направлении действия силы: 1 Н = 1 кгм/с2. Силы взаимодействия между материальными точками механической системы называются внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы, называется замкнутой (или изолированной). В механической системе, состоящей из многих тел, силы, действующие между этими телами, будут равны и противоположно направлены, т. е. геометрическая сумма внутренних сил равна нулю. В случае отсутствия внешних сил (рассматриваем замкнутую систему)
Вопрос 8 Момент инерции твердого тела
В качестве примера найдем момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси (рис. 1.18). Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и массой dm. Момент инерции каждого такого цилиндра dJ = r 2 dm (так как dr << r, то считаем, что расстояние всех точек цилиндра от оси равно r). Если ρ – плотность материала, объем 2πrhdr, то dm=2πrhρdr и dJ = 2πhρr3dr. Тогда момент инерции сплошного цилиндра но так как Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции J с относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы т тела на квадрат расстояния а между осями:
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.87.151 (0.007 с.) |

 При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами mi опишут окружности различных радиусов r, и имеют различные линейные скорости vi. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:
При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами mi опишут окружности различных радиусов r, и имеют различные линейные скорости vi. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова: .
.
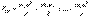 или,
или, 
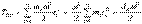
 В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:
В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения: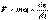

 (1.11), численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости, называется импульсом (количеством движения) этой материальной точки.
(1.11), численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости, называется импульсом (количеством движения) этой материальной точки.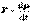
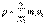 , – импульс системы. Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему.
, – импульс системы. Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему. т.е.
т.е. 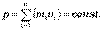

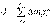 Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:
Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:

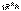 – объем цилиндра, то его масса
– объем цилиндра, то его масса 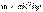 , а момент инерции
, а момент инерции