
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон сохранения движения центра масс.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Из теоремы о движении центра масс можно получить важные следствия. 1). Пусть сумма внешних сил, действующая на систему, равна нулю
Тогда из уравнения (6) следует, что Следовательно, если сумма всех внешних сил, действующих на систему, равна нулю, то центр масс этой системы движется с постоянной по модулю и направлению скоростью, то есть равномерно и прямолинейно. 2). Пусть сумма внешних сил не равна нулю, но эти силы таковы, что сумма их проекций на какую-нибудь ось (например ось Ох) равна нулю: Тогда первое из уравнений (6/) дает:
Следовательно, если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция скорости центра масс системы на эту ось есть величина постоянная. В частности, если в настоящий момент Пример. Движение по горизонтальной плоскости. При отсутствии трения человек с помощью своих мускульных усилий не мог двигаться вдоль горизонтальной плоскости, так как в этом случае сумма проекций на горизонтальную ось Ох всех приложенных к человеку внешних сил (сила тяжести и реакция плоскости) будет равна нулю и центр масс человека вдоль плоскости перемещаться не будет ( Если человек вынесет правую ногу, то левая его нога скользнет назад, а общий центр масс останется на месте. При наличии трения скольжению левой ноги назад будет препятствовать сила трения, которая в этом случае будет направлена вперед. Эта сила и будет внешней силой, которая позволяет человеку перемещаться вперед. Аналогично движение автомобиля.
Сила давления газа в двигателе является внутренней силой. Двигатель передает вращающий момент. При этом точка В стремиться скользнуть влево. Тогда на колесо будет действовать сила трения направленная вправо. Эта внешняя сила и позволит центру тяжести машины двигаться вперед. Рис. 4.2
Теорема об изменении количества движения системы. Количество движения системы.
Количеством движения системы будем называть векторную величину
Рис. 4.3
Как видно из рисунка вектор Найдем формулу с помощью, которой значительно легче вычислять
Беря от обеих частей производную по времени, получим
Отсюда находим
то есть количество движения системы равно произведению массы всей системы на скорость ее центра масс.
Рис. 4.4 Из формулы (8) видно, что если тело движется так, что центр масс остается неподвижным, то количество движения тела равно нулю. Например, количество движения вращающегося вокруг неподвижной оси будет равно нулю. Если движение сложное, то величина
Теорема об изменении количества движения. Рассмотрим систему, состоящую из «n» материальных точек, составим для этой системы дифференциальные уравнения движения (2) и сложим их почленно
Последняя сумма по свойству внутренних сил равна нулю. Кроме того,
Окончательно находим
Уравнение (9) выражает теорему об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения системы равна геометрической сумме всех действующих на систему внешних сил. В проекциях на координате оси будем иметь:
Найдем другое выражение теоремы. Пусть в момент t=0 количество движения равно
Уравнение (11) выражает теорему об изменении количества движения системы за некоторый промежуток времени равно сумме импульсов действующих на систему внешних сил за тот же промежуток времени. В проекциях на координатные оси:
|
|||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 651; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.174.253 (0.009 с.) |

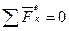 .
. или
или  .
. или
или  .
. , то в любой последующий момент
, то в любой последующий момент  ).
).
 , равную геометрической сумме (главному вектору) количества движения всех точек системы:
, равную геометрической сумме (главному вектору) количества движения всех точек системы: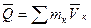 (7)
(7)
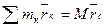 .
. или
или  .
. (8)
(8)
 .
. .
. (9)
(9) (10)
(10) , а в момент t1 становится
, а в момент t1 становится  . Тогда, умножая обе части равенства (9) на dt и интегрируя, получим:
. Тогда, умножая обе части равенства (9) на dt и интегрируя, получим: или
или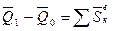 (11)
(11) (12)
(12)


