
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободные колебания без учёта сил сопротивления.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим точку М, движущуюся под действием одной только восстанавливающей силы F, направленной к неподвижному центру и пропорциональной расстоянию от этого центру.
Сила Рис. 3.7 Найдём закон движения точки С, составим дифференциальные уравнения движения
Деля обе части на m и вводя обозначение
приведём уравнение к виду
Уравнение (31) представляет собой дифференциальное уравнение свободных колебаний при отсутствии сопротивления. Решение этого однородного дифференциального уравнения ищут в виде Общее решение уравнения (31) имеет вид:
Если вместо постоянных
Скорость точки в рассматриваемом движении
Колебания, совершаемые точкой по закону (32), называется гармоническими колебаниями. График их при
Рис. 3.8
Рис. 3.9 фаза). Величина колебаний. Промежуток времени Т в течении которого точка совершает одно полное колебание, называется периодом колебаний. По истечении периода фаза изменяется на
Величина Отметим, что свободные колебания при отсутствии сопротивления обладают следующими свойствами: 1. амплитуда и начальная фаза колебаний зависят от начальных условий 2. частота k, а следовательно и период Т от начальных условий не зависят. Рассмотрим влияние постояннойсилы на свободные колебания точки. Пусть на точку М кроме восстанавливающей силы F действует постоянная по модулю и направлению сила Р. Величина силы F по прежнему пропорциональна расстоянию от центра О, т.е. Очевидно, что в этом случае положением точки М будет центр
или
Рис. 3.10 Примем Постоянная сила Р не изменяет характера колебаний, совершаемой точкой под действием восстанавливающей силы F, а только смещает центр этих колебаний в сторону действия силы Р на величину статического отклонения Из (36) и (30) имеем Тогда равенство (35) даст В частности, если Р – сила тяжести
Свободные колебания при сопротивлении, пропорциональном скорости (затухающие колебания) Рассмотрим, как влияет на свободные колебания сопротивления среды, считая, что сила сопротивления пропорциональна первой степени скорости: («–» указывает, что R против v). Пусть на точку при её движении действует восстанавливающая сила Тогда Дифференциальное уравнение будет
Рис. 3.11
Деля обе части на m, получим:
где обозначено
Уравнение (38) представляет собой дифференциальное уравнение
или по аналогии с равенством (30)
Входящая сюда постоянная и являются постоянными интегрирования и определяются по начальным условиям. Колебания, проходящие по закону (38) называют затухающими, т.к. благодаря множителю Промежуток времени
принято называть периодом затухающих колебаний.
Рис. 3.12 Формулу (42), если учесть равенство (35), можно представить в виде:
Из
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 587; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.145.41 (0.007 с.) |

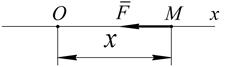 Проекции силы
Проекции силы 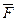 на ось Ox будет равна
на ось Ox будет равна 

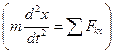
 (30)
(30)
 (31)
(31) . Полагая в уравнении (31)
. Полагая в уравнении (31)  .
. (32)
(32) и
и  ввести постоянные
ввести постоянные 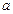 и
и  , такие, что
, такие, что  ,
,  , то получим:
, то получим: или
или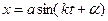 (33)
(33) (34)
(34)

 Рассмотрим точку B, равномерно на окружности из скольжения
Рассмотрим точку B, равномерно на окружности из скольжения  , определяется углом
, определяется углом  . Пусть постоянная угловая скорость вращение радиусов равна
. Пусть постоянная угловая скорость вращение радиусов равна 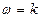 . Тогда в произвольный момент t угол
. Тогда в произвольный момент t угол  и легко увидеть, что проекция М точки В на диаметр движется по закону
и легко увидеть, что проекция М точки В на диаметр движется по закону  - фазой колебаний. Величина
- фазой колебаний. Величина  называется круговой частотой
называется круговой частотой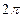 . Следовательно
. Следовательно  откуда
откуда (35)
(35) - частота колебаний.
- частота колебаний. .
. , отстраненной от оси О на расстояние
, отстраненной от оси О на расстояние  , которое определяется равенством
, которое определяется равенством

 (36)
(36) - статическое отклонение точки.
- статическое отклонение точки.
 , и учитывая
, и учитывая  или
или 
 (37)
(37) , то формула (34) имеет вид:
, то формула (34) имеет вид: (37/)
(37/) .
. .
. .
.
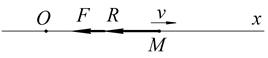
 (38)
(38) (39)
(39) (40)
(40) (41)
(41)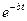 величина
величина  с течением времени убывает, стремясь к нулю.
с течением времени убывает, стремясь к нулю.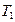 , равный периоду
, равный периоду  т.е. величину
т.е. величину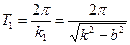 (42)
(42)
 (42/)
(42/)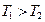 формул видно, что наличие сопротивления увеличивает период колебаний. Однако, когда сопротивление мало
формул видно, что наличие сопротивления увеличивает период колебаний. Однако, когда сопротивление мало  , то величиной
, то величиной 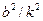 по сравнению с единицей можно пренебречь и считать
по сравнению с единицей можно пренебречь и считать  .
.


