
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложение колебаний одного направленияСодержание книги Поиск на нашем сайте
Бывают случаи, когда смещение x материальной точки представляет собой сумму смещений x1 + x2 + …, каждое из которых есть гармоническое колебание: Выяснение того, как выглядит сумма x1 + x2 + …, как её проще и понятней записать, называют сложением колебаний. Сложение колебаний удобно анализировать с помощью векторных диаграмм. Каждому колебанию соответствует свой вращающийся вектор. Сумма проекций вращающихся векторов есть прекция суммы векторов, а сумму векторов и проекцию её можно легко показать на векторной диаграмме. Рис. 4 поясняет случай сложения двух колебаний. Формулы, относящиеся к этому случаю:
Если частоты исходных колебаний одинаковы, то разность фаз Теперь на вопрос, как записать кинематическое уравнение гармонического колебания, можно ответить двояко: или как одно колебание с амплитудой A и некоторой начальной фазой На основании уравнения гармонических колебаний (32) скорость и ускорение материальной точки запишутся следующим образом:
Амплитуда скорости Av есть произведение амплитуды A на частоту
Д и н а м и к а к о л е б а н и я На основании формулы (36) сила, под действием которой точечное тело совершает гармонические колебания, есть сила типа F = – Cx, (37) где C можно представить как произведение массы и квадрата частоты:
Такую силу называют квазиупругой. Уравнение
Примером квазиупругой силы является сила пружины F = - kx, где k –– жёсткость пружины, показывающая силу пружины при её единичном удлинении (или сокращении). Если на закреплённой с одного конца пружине находится груз массой m, то он будет колебаться с частотой Ещё примером квазиупругой силы является результирующая сил, действующих на точечный груз, подвешенный на нити, отклонённой на малый угол от вертикали (математический маятник). Эта результирующая может быть записана как
Следующий пример – физический маятник. Им называется тело, способное вращаться вокруг оси, проходящей выше центра масс тела (рис. 6). Уравнению динамики вращательного движения можно придать вид
где I –– момент инерции относительно оси O; При малых углах отклонения это уравнение есть уравнение типа (39). В роли x выступает угол, в роли массы – I, в роли коэффициента C – множитель mgd. Поэтому для частоты и периода будут справедливы формулы::
Формулам (41) можно придать тот же вид, что и формулам Гюйгенса, если величину I/md, имеющую размерность длины, обозначить далее через lпр. Величину lпр называют приведённой длиной физического маятника:
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.60.19 (0.005 с.) |

 .
. .
.  . (33)
. (33) . (34)
. (34) можно заменить разностью начальных фаз
можно заменить разностью начальных фаз  .
. , или как сумму двух колебаний с амплитудами a и b
, или как сумму двух колебаний с амплитудами a и b  , причём A2 = a2 +b2,
, причём A2 = a2 +b2,  .
. , (35)
, (35)  . (36)
. (36)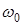 . Ускорение пропорционально смещению x со знаком минус и коэффициент пропорциональности есть квадрат частоты.
. Ускорение пропорционально смещению x со знаком минус и коэффициент пропорциональности есть квадрат частоты. . (38)
. (38)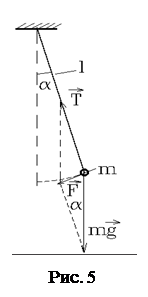
 (39)
(39) есть уравнение динамики простого гармонического колебания (дифференциальное уравнение гармонического колебания).
есть уравнение динамики простого гармонического колебания (дифференциальное уравнение гармонического колебания). .
. (рис. 5). Знак "–" учитывает то, что сила направлена в сторону уменьшения угла отклонения. При малых углах отклонения смещение можно считать прямым отрезком x и, кроме того,
(рис. 5). Знак "–" учитывает то, что сила направлена в сторону уменьшения угла отклонения. При малых углах отклонения смещение можно считать прямым отрезком x и, кроме того, 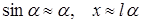 . И тогда получается F=–(mg/l)x. В роли коэффициента C здесь выступает mg/l. Для частоты и периода имеем (формулы Гюйгенса)
. И тогда получается F=–(mg/l)x. В роли коэффициента C здесь выступает mg/l. Для частоты и периода имеем (формулы Гюйгенса) . (40)
. (40)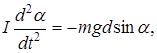
 – соответственно угловое ускорение и плечо силы тяжести; точка С – центр масс.
– соответственно угловое ускорение и плечо силы тяжести; точка С – центр масс. (41)
(41) . (41l)
. (41l)


