
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы для механической системыСодержание книги Поиск на нашем сайте
Законы для механической системы Строго говоря, для описания движения системы из N материальных точек необходимо записать N векторных дифференциальных уравнений, решить их с учётом некоторых начальных условий, проанализировать все решения и сделать суждения. Математически такая задача часто бывает неразрешимой. Поэтому всякий результат (вывод), полученный в отношении движения системы как целого, представляет определённую ценность. Отдельные такие выводы и результаты называются законами движения механической системы. К ним относятся, например, закон изменения импульса, закон сохранения импульса; закон изменения энергии, закон сохранения энергии; закон изменения момента импульса, закон сохранения момента импульса.
З а к о н и з м е н е н и я и м п у л ь с а. З а к о н с о х р а н е н и я и м п у л ь с а Импульсом системы называется вектор В производную d P /dt войдут слагаемые mid v i /dt. По закону Ньютона каждое такое слагаемое можно приравнять результирующей внешней силе F iи результирующей внутренней силе f iсо стороны остальных частиц. При суммировании F i и f i сумма всех внутренних сил будет равна нулю, так как, например, для силы f 12 согласно третьему закону Ньютона найдётся равная по модулю и противоположная сила f 21. Получается, что
где F –– результирующая всех внешних сил, действующих на систему. Это и есть закон изменения импульса для механической системы. Импульс системы можно представить как произведение общей массы m системы на некоторую скорость V C, которую называют скоростью центра масс системы. Формулировка закона изменения импульса в терминах центра масс
От закона изменения импульса легко перейти к закону сохранения импульса: F i = 0, F = 0, P = const. (14) Механическая система, на которую не действуют никакие внешние силы, называется замкнутой системой. Сила есть взятый со знаком «-» градиент потенциальной энергии. Введение потенциальной энергии позволяет сформулировать закон сохранения энергии для материальной точки:
Законы для механической системы Строго говоря, для описания движения системы из N материальных точек необходимо записать N векторных дифференциальных уравнений, решить их с учётом некоторых начальных условий, проанализировать все решения и сделать суждения. Математически такая задача часто бывает неразрешимой. Поэтому всякий результат (вывод), полученный в отношении движения системы как целого, представляет определённую ценность. Отдельные такие выводы и результаты называются законами движения механической системы. К ним относятся, например, закон изменения импульса, закон сохранения импульса; закон изменения энергии, закон сохранения энергии; закон изменения момента импульса, закон сохранения момента импульса.
З а к о н и з м е н е н и я и м п у л ь с а. З а к о н с о х р а н е н и я и м п у л ь с а Импульсом системы называется вектор В производную d P /dt войдут слагаемые mid v i /dt. По закону Ньютона каждое такое слагаемое можно приравнять результирующей внешней силе F iи результирующей внутренней силе f iсо стороны остальных частиц. При суммировании F i и f i сумма всех внутренних сил будет равна нулю, так как, например, для силы f 12 согласно третьему закону Ньютона найдётся равная по модулю и противоположная сила f 21. Получается, что
где F –– результирующая всех внешних сил, действующих на систему. Это и есть закон изменения импульса для механической системы. Импульс системы можно представить как произведение общей массы m системы на некоторую скорость V C, которую называют скоростью центра масс системы. Формулировка закона изменения импульса в терминах центра масс
От закона изменения импульса легко перейти к закону сохранения импульса: F i = 0, F = 0, P = const. (14) Механическая система, на которую не действуют никакие внешние силы, называется замкнутой системой.
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 162; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.57.57 (0.005 с.) |

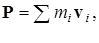 где mi, v i –– масса и скорость i-й материальной точки системы.
где mi, v i –– масса и скорость i-й материальной точки системы.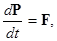 (12)
(12)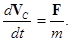 (13)
(13)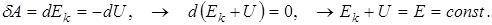 (19)
(19)


