
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоское движение твёрдого тела.Содержание книги Поиск на нашем сайте
При обсуждении кинематики твёрдого тела уже отмечалось, что перемещение любой точки тела можно представить как перемещение центра масс тела и перемещение по дуге некоторого радиуса относительно центра масс. Соответственно работу силы, приложенной в некоторой точке твёрдого тела, можно представить как сумму работы силы на перемещении центра масс и работы на перемещении точки приложения силы относительно центра масс. В соответствии с этим кинетическую энергию плоского движения можно записать в виде
Формулу (29) можно применить к случаю вращения тела около закреплённой оси. Скорость центра масс можно представить как произведение угловой скорости на расстояние d от центра масс до оси вращения. Тогда получится, что
С другой стороны, эту же энергию можно записать как
где I –– момент инерции тела относительно закреплённой оси вращения. Между моментами инерции IC и I должно быть соотношение I = IC + md2. (30) Соотношение (30) выражает теорему Штейнера: Момент инерции относительно некоторой оси вращения равен сумме момента инерции относительно оси, проходящей через центр масс и параллельной данной, и произведения массы тела на квадрат расстояния между осями.
M = Fl, где l –– расстояние между линиями действия сил пары (плечо пары). Второе уравнение динамики плоского движения:
Таким образом, динамика плоского движени твёрдого тела выражается уравнениями (13) и (31).
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ К и н е м а т и к а к о л е б а т е л ь н о г о д в и ж е н и я Колебательные движения –– это движения, повторяющиеся во времени. Простейшей периодической функцией является гармоническая функция cos или sin. Простейшим колебанием является гармоническое колебание, когда в формуле для координаты время входит под знак косинуса или синуса:
Правую часть (32) можно истолковать как проекцию на ось x вектора длиной A, вращающегося в плоскости xy с угловой скоростью
|
|||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 167; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.25.185 (0.009 с.) |

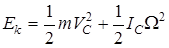 . (29)
. (29) .
.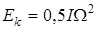 ,
, Что можно сказать о уравнениях динамики плоского движения твёрдого тела? Одно из уравнений – это уравнение (13) движения центра масс. Ещё одно уравнение должно описывать движение относительно центра масс. Обратимся к рис. 3, плоскость которого параллельна вектору внешней силы F. Представим, что в центре масс действуют две равные по модулю, но противоположные силы F l = F и F ll =- F. Введение этих сил не вызовет изменения движения. Теперь три силы можно перегруппировать как F l и F + F ll. Сила F l вызовет только ускорение центра масс в соответствии с уравнением (13). Силы F и F ll не могут вызвать ускорение центра масс, так как результирующая их равна нулю. Они могут вызвать только движение относительно центра масс, то есть вращение в плоскости этих сил. Такие силы называются парой сил. Величину момента пары сил можно подсчитывать не по общей, а по более простой формуле
Что можно сказать о уравнениях динамики плоского движения твёрдого тела? Одно из уравнений – это уравнение (13) движения центра масс. Ещё одно уравнение должно описывать движение относительно центра масс. Обратимся к рис. 3, плоскость которого параллельна вектору внешней силы F. Представим, что в центре масс действуют две равные по модулю, но противоположные силы F l = F и F ll =- F. Введение этих сил не вызовет изменения движения. Теперь три силы можно перегруппировать как F l и F + F ll. Сила F l вызовет только ускорение центра масс в соответствии с уравнением (13). Силы F и F ll не могут вызвать ускорение центра масс, так как результирующая их равна нулю. Они могут вызвать только движение относительно центра масс, то есть вращение в плоскости этих сил. Такие силы называются парой сил. Величину момента пары сил можно подсчитывать не по общей, а по более простой формуле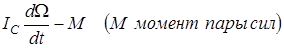 . (31)
. (31)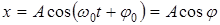 . (32)
. (32)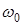 . Начальный угол наклона этого вектора к оси x –
. Начальный угол наклона этого вектора к оси x –  . Поэтому
. Поэтому  называют циклической частотой колебаний. Величины A и
называют циклической частотой колебаний. Величины A и 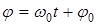 – фазой колебания. Изображение упомянутого вектора называют векторной диаграммой колебания.
– фазой колебания. Изображение упомянутого вектора называют векторной диаграммой колебания.


