
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В консервативных системах полная механическая энергия, равная сумме кинетической и потенциальной энергий, сохраняется.Содержание книги
Поиск на нашем сайте
Эта формулировка подходит и для системы из N материальных точек. В этом случае потенциальная энергия может быть подразделена на потенциальную энергию в поле внешних консервативных сил и потенциальную энергию взаимодействия частиц между собой. Аналогично, кинетическая энергия системы может быть представлена как сумма кинетической энергии движения системы как целого (половина произведения массы всей системы на квадрат скорости центра масс) и кинетической энергии движения частиц относительно центра масс. В случае, если внешнее силовое поле является однородным (как, например, поле силы тяжести), то потенциальную энергию можно записать как энергию тела с массой всей системы и с координатами центра масс. Закон изменения механической энергии формулируется для случая, когда создающие силовое поле внешние тела движутся в выбранной системе отсчёта. Соответствующее этому силовое поле изменяется со временем. Силы называют сторонними, или неконсервативными. Закон изменения энергии:
Изменение полной энергии равно работе сторонних (неконсервативных) сил. К сторонним силам можно отнести и диссипативные силы, действующие внутри системы.
З а к о н и з м е н е н и я м о м е н т а и м п у л ь с а. З а к о н с о х р а н е н и я м о м е н т а и м п у л ь с а Возьмём случай одной материальной точки. Вектор L = [ r, m v ] называется моментом импульса материальной точки. Производная по времени от этой величины будет
Для замкнутой механической системы F i = 0, M = 0, L = const. (22) То есть в замкнутой механической системе момент импульса есть величина постоянная – закон сохранения момента импульса. Этот закон нередко используется при решении задач. Если для конкретной механической системы удалось заметить, что при некотором выборе начала отсчёта момент внешних сил отсутствует или пренебрежимо мал, то момент импульса этой системы надо считать постоянным. Скажем, для системы из двух материальных точек должно быть m1[ r 1, v 1] + m2[ r 2, v 2] = const. Для материальной точки в поле действия центральной силы должно выполняться условие [ r, v ] = const, где r – радиус-вектор материальной точки относительно силового центра. Последнее равенство означает постоянство секторной скорости – площади, “замазываемой” радиус-вектором за единицу времени. На рис. 1 видно, что
В р а щ а т е л ь н о е д в и ж е н и е т в ё р д о г о т е л а. П л о с к о е д в и ж е н и е Законы сохранения и изменения момента импульса особенно ярко проявляются при плоском движении твёрдого тела. Частным случаем плоского движения является вращательное движение, когда частицы движутся по окружностям разных радиусов, центры которых лежат на одной прямой –– оси вращения. Ниже будут рассмотрены простейшие случаи, иллюстрирующие законы изменения и сохранения момента мпульса, сохранения энергии.
для Lz получим Но Сумма
При равномерном вращении величина Lz сохраняется. В общем случае согласно уравнению (21) должно быть dLz/dt = Mz, то есть равномерное вращение будет при условии Mz = 0. Если же момент сил Mz отличен от нуля, то
Уравнение (24) называют уравнением динамики вращательного движения. Все величины имеют прозрачный смысл. Iz –– мера инертности при вращательном движении, Mz –– мера воздействия на вращающееся тело, Случай Формулу, подобную (23), можно записать и для случая вращения симметричного твёрдого тела вокруг своей оси симметрии:
где IC –– момент инерции тела относительно оси симметрии, а значит, относительно оси, проходящей через центр масс. Ось симметрии является свободной осью. Тело может вращаться вокруг такой оси, даже если ось не закреплена. В теоретической механике доказывается, что в любом твёрдом теле (произвольной формы) есть три взаимно перпендикулярные свободные оси (главные оси). При отсутствии момента внешних сил вращающееся вокруг свободной оси тело сохраняет величину угловой скорости и ориентацию оси вращения. Назовём ещё примеры, иллюстрирующие закон сохранения момента импульса. 1. Свободно вращающееся вокруг главной оси тело в какой-то момент резко меняет момент инерции I1 на I2 . Должно выполняться соотношение
где 2. Соосно вращающиеся тела могут взаимодействовать друг с другом при отсутствии моментов внешних сил. Должно выполняться условие
где i –– номер вращающегося тела.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 222; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.188.223 (0.008 с.) |

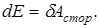 (20)
(20) так как векторное произведение векторов d r /dt и v равно нулю. Множитель md v /dt есть сила F, действующая на материальную точку. Вектор M = [ r, F ] называют вектором момента силы. Отсюда получается уравнение
так как векторное произведение векторов d r /dt и v равно нулю. Множитель md v /dt есть сила F, действующая на материальную точку. Вектор M = [ r, F ] называют вектором момента силы. Отсюда получается уравнение (21)
(21) Оно легко обобщается на случай системы материальных точек, где момент импульса системы есть векторная сумма всех Li – моментов импульса отдельных материальных точек системы. В этом случае под M надо понимать результирующий момент всех внешних сил, так как результирующий момент внутренних сил равен нулю на основании третьего закона Ньютона. Уравнение (21) и называют законом изменения момента импульса.
Оно легко обобщается на случай системы материальных точек, где момент импульса системы есть векторная сумма всех Li – моментов импульса отдельных материальных точек системы. В этом случае под M надо понимать результирующий момент всех внешних сил, так как результирующий момент внутренних сил равен нулю на основании третьего закона Ньютона. Уравнение (21) и называют законом изменения момента импульса. есть высота заштрихованного треугольника, а vdt – основание его. Произведение этих величин есть величина векторного произведения [ r, v ] и вместе с тем это удвоенная площадь, замазанная радиус-вектором за время dt.
есть высота заштрихованного треугольника, а vdt – основание его. Произведение этих величин есть величина векторного произведения [ r, v ] и вместе с тем это удвоенная площадь, замазанная радиус-вектором за время dt. Простейшее движение твёрдого тела – вращение вокруг закреплённой оси. При выборе начала отсчёта на оси вращения момент импульса принадлежащей твёрдому телу i-частицы направлен под некоторым углом
Простейшее движение твёрдого тела – вращение вокруг закреплённой оси. При выборе начала отсчёта на оси вращения момент импульса принадлежащей твёрдому телу i-частицы направлен под некоторым углом  к вектору угловой скорости
к вектору угловой скорости  (рис. 2). При равномерном вращении тела (
(рис. 2). При равномерном вращении тела ( ) вектор L i частицы будет описывать конус с углом 2
) вектор L i частицы будет описывать конус с углом 2  . Учитывая, что
. Учитывая, что  ,
, .
.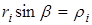 есть радиус вращения i-й частицы. Для проекции момента импульса всего твёрдого тела получается
есть радиус вращения i-й частицы. Для проекции момента импульса всего твёрдого тела получается  .
. называется моментом инерции твёрдого тела относительно данной оси вращения. Таким образом
называется моментом инерции твёрдого тела относительно данной оси вращения. Таким образом (23).
(23). . (24)
. (24) –– мера “отклика” вращающегося тела на воздействие. Момент сил относительно оси вращения Mz (проекция вектора M на ось z) обусловлен касательными силами (силами, перпендикулярными оси вращения).
–– мера “отклика” вращающегося тела на воздействие. Момент сил относительно оси вращения Mz (проекция вектора M на ось z) обусловлен касательными силами (силами, перпендикулярными оси вращения). есть проявление закона сохранения момента импульса.
есть проявление закона сохранения момента импульса. , (25)
, (25) , (26)
, (26) – угловые скорости до и после смены момента инерции.
– угловые скорости до и после смены момента инерции. , (27)
, (27)


