
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория пар сил. Теоремы о парахСодержание книги Поиск на нашем сайте
Пара сил — совокупность двух параллельных друг другу сил равных по величине и направленных в противоположные стороны. Пара сил не может быть более упрощена (заменена одной силой) и представляет собой новую силовую характеристику механического взаимодействия. Теорема о моменте пары сил. Момент пары сил не зависит от выбора центра привидения и равен произведению любой из сил пары на плечо пары, взятый со знаком «+» при вращении пары против часовой стрелки или со знаком «-» при вращении по часовой. Плечо пары сил — длина перпендикуляра опущенного из любой точки линии действия одной силы к линии действия другой силы этой пары. Теорема об эквивалентности пар сил в плоскости. Пары сил, лежащие в одной плоскости, эквивалентны, если их моменты численно равны и одинаковы по знаку. Следствие. Пару сил, не изменяя ее действие на твердое тело, можно переносить в любое место в плоскости ее действия, поворачивать ее плечо на любой угол, а также изменять это плече и модули сил, не изменяя величины ее момента и направления вращения. Следовательно, основной характеристикой пары сил является ее момент. Теорема об эквивалентности пар сил в пространстве. Пары сил в пространстве эквивалентны, если их моменты геометрически равны. Следствие. Не изменяя действия пары сил на твердое тело, пару сил можно переносить в любую плоскость, параллельную плоскости ее действия, а также изменять ее силы и плечо, сохраняя неизменным модуль и направление ее момента. Вектор момента пары сил можно переносить в любую точку, т.е. момент пары сил является свободным вектором. Вектор момента пары сил определяет все три ее элемента: положение плоскости действия пары, направление вращения и числовое значение момента. Теорема о сложении пар сил на плоскости. Систему пар сил можно заменить парой сил, момент которой равен алгебраической сумме моментов исходных пар. Кинематическое состояние тела не изменяется. Условие равновесия системы пар сил:
18. Статические инварианты и динамические винты Инварианты системы сил — величины, не зависящие от выбора центра приведения. Первый векторный инвариант — главный вектор системы сил Главный момент не является инвариантом т.к. зависит от центра привидения. Однако существует величина, связанная с главным вектором и не зависящая от центра приведения. Однако существует величина, связанная с главным вектором и не зависящая от центра привидения: 1) 2) 3) Второй скалярный инвариант — скалярное произведение главного вектора на вектор главного момента.
Главный минимальный момент также инвариантная величина:
Динамический винт — совокупность действующих на тело силы F и пары сил с моментом М, лежащей в плоскости перпендикулярной силе F. К динамическому винту приводится в наиболее общем случае произвольная система сил, действующих на тело. Дальнейшее упрощение динамического винта не возможно, т.е. его нельзя заменить одной силой и одной парой сил. Можно лишь сложив F с одной из сил пары привести его к двум скрещивающимся силам.
Центры тяжести простейших фигур
Фермы. Методы расчета ферм
Способ вырезания узлов. Суть способа заключается в том, что мысленно вырезают каждый узел фермы, прикладывают к нему известные силы и реакции стержней, которые направляют от узла, т.к. неизвестно какие стержни фермы растянуты, а какие сжаты, изначально полагают, что все стержни растянуты, а затем составляются уравнения равновесия сил, приложенных к каждому узлу. Расчет фермы начинают с узлов, к которым приложено не более двух неизвестных сил для плоской фермы, и не более трех для пространственной. Метод Риттера. Ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из которых) требуется определить усилия, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, т. е. считая их растянутыми. Затем составляют уравнения моментов относительно точек Риттера (точка пересечения двух из трех перерезанных стержней). Из полученных уравнений определяются усилия в стержнях.
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.177.179 (0.006 с.) |

 .
.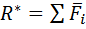 .
.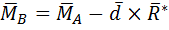

 .
. .
. .
.
 Центр тяжести дуги окружности.
Центр тяжести дуги окружности.

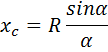 Центр тяжести объема четырехгранной пирамиды.
Центр тяжести объема четырехгранной пирамиды.




 Центр тяжести площади сектора.
Центр тяжести площади сектора.

 Центр тяжести конуса.
Центр тяжести конуса.

 Фермой называется геометрически не изменяемая шарнирно-стрежневая конструкция. Если все оси фермы лежат в одной плоскости, то ферму называют плоской. Точки, в которых сходятся оси стержней, называют узлами фермы, а те узлы, которыми ферма опирается на основание, называются опорными узлами. Стержни плоской фермы, расположенные по верхнему контуру, образуют верхний пояс фермы, а расположенные по нижнему контуру — нижний пояс фермы. Вертикальные стержни называются стойками, а наклонные — раскосами.
Фермой называется геометрически не изменяемая шарнирно-стрежневая конструкция. Если все оси фермы лежат в одной плоскости, то ферму называют плоской. Точки, в которых сходятся оси стержней, называют узлами фермы, а те узлы, которыми ферма опирается на основание, называются опорными узлами. Стержни плоской фермы, расположенные по верхнему контуру, образуют верхний пояс фермы, а расположенные по нижнему контуру — нижний пояс фермы. Вертикальные стержни называются стойками, а наклонные — раскосами.


