Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные задачи кинематики точки и телаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Основная задача кинематики точки заключается в разработке способов задания движения точки и методов определения основных кинематических характеристик движения. Основная задача кинематики твердого тела заключается в разработке способов задания движения и методов, позволяющих на основе небольшого числа характеристик, общих для всех точек находить кинематические характеристики каждой точки тела. Задать движение точки, значит указать математический аппарат, с помощью которого в любой заданный наперед момент времени определить положение точки в пространстве.
3. Векторный, координатный и естественный способ задания движения точки Задать движение точки, значит задать математический аппарат, с помощью которого можно в любой заданный наперед момент времени определить положение точки в пространстве.
С течением времени точка изменяет свое положение в пространстве тела отсчета. Поэтому радиус-вектор изменяется как по направлению, так и по величине и представляет собой некоторую векторную функцию скалярного аргумента t,
Если функции известны или заданы, то речь идет о координатном способе задания движения.
С течением времени дуговая координата изменяется и представляет собой некоторую функцию
4. Определение скорости и ускорения при векторном способе задания движения. При векторном способе задания движения положение движущейся точки в каждый момент времени определяется радиус-вектором
Вектор скорости точки Допустим, что в начальный момент точка имеет скорость
Вектор ускорения направлен по касательной к годографу скорости — геометрическому месту концов векторов скорости движущейся точки, отложенных от одной и той же произвольной точки пространства.
5. Определение скорости и ускорения при координатном способе задания движения точки Пусть заданы уравнения движения точки:
Вычислив проекции скорости на оси декартовых координат, можно определить модуль и направление вектора скорости по следующим формулам:
Вычислив проекции ускорения на координатные оси можно определить модуль и направление ускорения по следующим формулам:
6. Определение скорости и ускорения при естественном способе задания движения точки
Условимся алгебраическую величину скорости обозначать символом
т.е. модуль скорости равен абсолютному значению производной от дуговой координаты точки по времени.
Проекция ускорения точки на касательную равна второй производной от дуговой координаты точки по времени или первой производной от алгебраической величины скорости точки по времени.
Поступательное движение тела. Задание движения. Распределение скоростей и ускорений точек тела Поступательным движением твердого тела называется такое движение, при котором любая прямая, соединяющая две точки тела, движется параллельно самой себе. Теорема. Все точки твердого тела, движущегося поступательно, описывают одинаковые (совпадающие при наложении) траектории и в каждый момент времени имеют геометрически равные скорости и ускорения. Уравнениями поступательного движения твердого тела являются уравнения движения любой точки этого тела — обычно уравнения движения его центра тяжести:
Общие для всех точек твердого тела, движущегося поступательно, скорость
Вращательное движение. Задание движения Вращательным называется такое движение тела, при котором остаются неподвижными все его точки, лежащие на некоторой прямой, называемой осью вращения. При этом движении все остальные точки тела движутся в плоскостях перпендикулярных оси вращения, и описывают окружности, центры которых лежат на этой оси. При вращении тела угол поворота Величина, характеризующая быстроту изменения угла поворота
Величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорением тела.
Уравнение равномерного вращения тела. Вращение тела с постоянной скоростью называется равномерным.
Уравнение равнопеременного вращения тела. Вращение тела, при котором угловое ускорение постоянно, называют равнопеременным вращением.
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 845; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.199.242 (0.011 с.) |

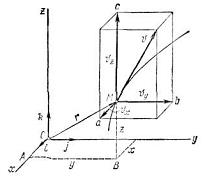
 Возьмем тело отсчета. Выберем на нем некоторую точку О. Чтобы определить положение точки М в пространстве тела отсчета введем в рассмотрение радиус-вектор.
Возьмем тело отсчета. Выберем на нем некоторую точку О. Чтобы определить положение точки М в пространстве тела отсчета введем в рассмотрение радиус-вектор. . Если функция
. Если функция  задана или известна, то речь идет о векторном способе задания точки.
задана или известна, то речь идет о векторном способе задания точки. Введем в рассмотрение тело отсчета. С телом отсчета жестко свяжем декартовую систему координат. Чтобы определить положение точки М в пространстве тела отсчета достаточно знать ее координаты. С течением времени координаты точки будут изменяться и представлять собой некоторые функции скалярного аргумента t.
Введем в рассмотрение тело отсчета. С телом отсчета жестко свяжем декартовую систему координат. Чтобы определить положение точки М в пространстве тела отсчета достаточно знать ее координаты. С течением времени координаты точки будут изменяться и представлять собой некоторые функции скалярного аргумента t.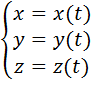 .
. Пусть нам известна траектория движения точки. На этой траектории выбираем произвольную точку О. Положение точки М на траектории можно задать с помощью дуговою координаты.
Пусть нам известна траектория движения точки. На этой траектории выбираем произвольную точку О. Положение точки М на траектории можно задать с помощью дуговою координаты. Если функция задана речь идет о естественном способе задания движения точки.
Если функция задана речь идет о естественном способе задания движения точки. который является функцией времени
который является функцией времени  При перемещении точки ее радиус-вектор получает приращение
При перемещении точки ее радиус-вектор получает приращение  . Отношение вектора перемещения
. Отношение вектора перемещения  к промежутку времени
к промежутку времени 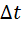 , в течение которого совершается это перемещение, представляет собой вектор средней скорости
, в течение которого совершается это перемещение, представляет собой вектор средней скорости  движения точки:
движения точки: 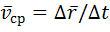 .
. Вектор скорости точки в данный момент времени равен производной от радиус-вектора точки по времени:
Вектор скорости точки в данный момент времени равен производной от радиус-вектора точки по времени:
 направлен по касательной к траектории в сторону движения точки.
направлен по касательной к траектории в сторону движения точки.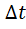 получает приращение
получает приращение  . Разделив приращение
. Разделив приращение  на промежуток времени
на промежуток времени 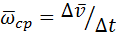 . Вектор ускорения точки равен первой производной от скорости или второй производной от радиус-вектора точки по времени.
. Вектор ускорения точки равен первой производной от скорости или второй производной от радиус-вектора точки по времени.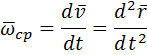

 Проекции скорости точки на неподвижные оси декартовых координат равны первым производным от соответствующих координат точки по времени:
Проекции скорости точки на неподвижные оси декартовых координат равны первым производным от соответствующих координат точки по времени:
 ;
;  ;
;  ;
; .
.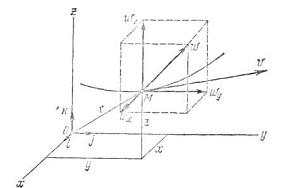 Проекции ускорения точки на неподвижные оси декартовых координат равны вторым производным от соответствующих координат точкипо времени или первым производным по времени от проекций скорости на соответствующие оси.
Проекции ускорения точки на неподвижные оси декартовых координат равны вторым производным от соответствующих координат точкипо времени или первым производным по времени от проекций скорости на соответствующие оси.
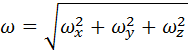 ;
;  ;
;  ;
; 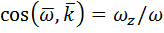 .
.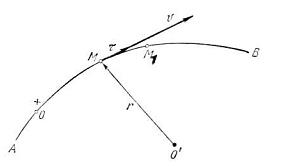 Определим скорость точки, если известна ее траектория AB, начало и направление отсчета дуговой координаты, и уравнение движения точки
Определим скорость точки, если известна ее траектория AB, начало и направление отсчета дуговой координаты, и уравнение движения точки 
 , а модуль скорости — буквой
, а модуль скорости — буквой  . Тогда:
. Тогда: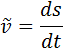
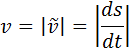



 ускорение
ускорение  называют скоростью и ускорением поступательного движения твердого тела.
называют скоростью и ускорением поступательного движения твердого тела. изменяется в зависимости от времени:
изменяется в зависимости от времени:  .
. с течением времени называется угловой скоростью тела.
с течением времени называется угловой скоростью тела.