
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия Пространственной системы произвольно расположенных силСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Произвольной пространственной системой сил называется система сил, линии действия которых не лежат в одной плоскости. Отсюда вытекает условие равновесия произвольной пространственной системы сил.
В геометрической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент системы равнялись нулю R = 0, Mo = 0. В аналитической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на три координатные оси и суммы моментов всех сил относительно этих осей были равны нулю
ΣFkx = 0, ΣFky = 0, ΣFkz = 0, Mx(Fk) = 0, My(Fk) = 0, Mz(Fk) = 0. Центр тяжести. Способы определение центра тяжести. Координаты центра тяжести плоского тела и составленных сечений. Центр тяжести Центр тяжести тела - точка приложения силы тяжести (равнодействующей гравитационных сил).
Центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Определение центра тяжести Определение центра тяжести произвольного тела путем последовательного сложения сил, действующих на отдельные его части,— трудная задача; она облегчается только для тел сравнительно простой формы. Пусть тело состоит только из двух грузов с массами m1 и m2, соединенных стержнем (рис. 126). Если масса стержня мала по сравнению с массами m1 и m2, то ею можно пренебречь. На каждую из масс действует сила тяжести: P1=m1g, Р2=m2g; обе они направлены вертикально вниз, т. е. параллельно друг другу. Как мы уже знаем, равнодействующая двух параллельных сил приложена в точке О, которая определяется из условия
Следовательно, центр тяжести делит расстояние между двумя массами в отношении обратном отношению масс. Если это тело подвесить в точке О, оно останется в равновесии.
Определение координат центра тяжести
Центр тяжести однородных плоских тел (плоских фигур) Очень часто приходится определять центр тяжести различных плоских тел и геометрических плоских фигур сложной формы. Для плоских тел можно записать: V = Ah, где А — площадь фигуры, h — ее высота. Тогда после подстановки в записанные выше формулы получим:
где Ак — площадь части сечения; хк, ук — координаты ЦТ частей сечения. Выражение Координаты центра тяжести сечения можно выразить через статический момент:
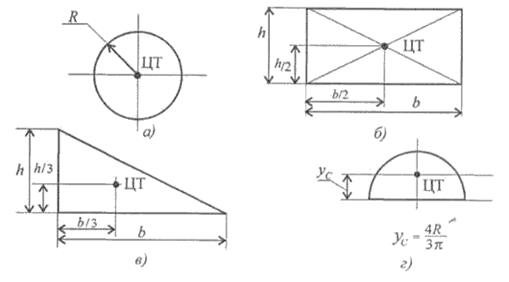
Оси, проходящие через центр тяжести, называются центральными осями. Статический момент относительно центральной оси равен нулю. Определение координат центра тяжести плоских фигур Примечание. Центр тяжести симметричной фигуры находится на оси симметрии. Центр тяжести стержня находится на середине высоты. Положения центров тяжести простых геометрических фигур могут быть рассчитаны по известным формулам (рис. 8.3: а) — круг; б) — квадрат, прямоугольник; в) — треугольник; г) — полукруг).
Скорость точки Скорость точки
Ускорение точки Ускорение точки
|
|||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |




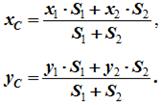
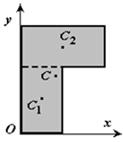 Рисунок 1.8
5Дополнение (метод отрицательных площадей или объемов). Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
Рисунок 1.8
5Дополнение (метод отрицательных площадей или объемов). Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
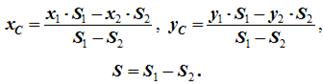
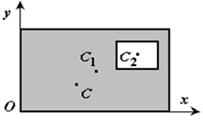 Рисунок 1.9
Рисунок 1.9
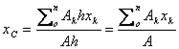 ;
; 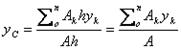 ;
;  ,
,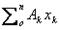 называют статическим моментом площади (Sy.).
называют статическим моментом площади (Sy.).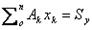 ;
; 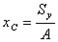 ;
; 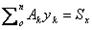 ;
; 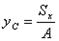 .
.
 тогда
тогда
 средняя скорость точки за промежуток времени Dt. Скорость точки в данный момент времени
средняя скорость точки за промежуток времени Dt. Скорость точки в данный момент времени
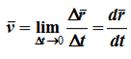
 Скорость точки – это кинематическая мера ее движения, равная производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета. Вектор скорости направлен по касательной к траектории точки в сторону движения.
Скорость точки – это кинематическая мера ее движения, равная производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета. Вектор скорости направлен по касательной к траектории точки в сторону движения.
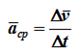 характеризует изменение вектора скорости за малый промежуток времени Δt. Ускорение точки в данный момент времени
характеризует изменение вектора скорости за малый промежуток времени Δt. Ускорение точки в данный момент времени

 Ускорение точки – это мера изменения ее скорости, равная производной по времени от скорости этой точки или второй производной от радиус-вектора точки по времени. Ускорение характеризует изменение вектора скорости по величине и направлению и направлено в сторону вогнутости траектории.
Ускорение точки – это мера изменения ее скорости, равная производной по времени от скорости этой точки или второй производной от радиус-вектора точки по времени. Ускорение характеризует изменение вектора скорости по величине и направлению и направлено в сторону вогнутости траектории.



