
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение эпюр крутящих моментов.Содержание книги
Поиск на нашем сайте Стержень испытывает кручение, если в его поперечных сечениях возникают крутящие моменты, т.е. моменты, лежащие в плоскости сечения. Обычно эти крутящие моменты Тк возникают под действием внешних моментов Т (рис. 2.1). Внешние моменты передаются на вал, как правило, в местах посадки на него шкивов, зубчатых колес и т.п. Однако и поперечная нагрузка, смещенная относительно оси стержня, вызывает крутящие моменты (рис. 2.2), но в указанном слечае
в поперечных сечениях наряду с крутящими моментами возникают и другие внутренние усилия - поперечные силы и изгибающие моменты. Вращающиеся и работающие на кручение стержни называют валами. Вместо аксонометрического изображения будем применять главным образом плоское, как более простое. Внешние скручивающие моменты и внутренние крутящие моменты будем изображать в виде линии с двумя кружочками. В одном из них будем ставить точку, обозначающую начало стрелки (на нас), в другом - крестик, обозначающий конец стрелки, направленный от нас (рис. 2.3). Для определения крутящих моментов Тк возникающих в сечениях вала под действием внешних скручивающих моментов или поперечной нагрузки, будем применять метод сечений. Сделаем мысленный разрез стержня (рис. 2.3), например по а - а, отбросим одну часть стержня, в данном случае левую, и рассмотрим равновесие оставшейся правой части.
Взаимодействие частей стержня заменим крутящим моментом Тк, уравновешивающим внешний момент Т. Для равновесия отсеченной части необходимо, чтобы алгебраическая сумма всех моментов, действующих на нее, была равна нулю. Отсюда в рассматриваемом случае получим, что Тк = Т. Если на отсеченную часть будет действовать несколько внешних моментов, то, проведя аналогичное рассуждения, можно убедиться, что крутящий момент в сечении численно равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения. Для наглядного представления о характере распределения и величине крутящих моментов по длине стержня строят эпюры (графики) этих моментов. Построение их вполне аналогично построению эпюр продольных сил при растяжении или сжатии. Для построения эпюр необходимо условиться о правиле знаков. Общепринятого правила знаков для крутящих моментов не существует. Может быть принято любое правило знаков. Важно лишь принятое правило выдержать на всем протяжении эпюры.
Примем следующее правило знаков (рис. 2.4). Крутящий момент в сечении а - а считается положительным, когда внешний момент вращает отсеченную часть против часовой стрелки, если смотреть на отсеченную часть со стороны сечения. Если же внешний момент вращает отсеченную часть по часовой стрелке (при взгляде со стороны сечения), то крутящий момент в сечении будем считать отрицательным. Построение эпюры крутящих моментов поясним на следующем примере (рис. 2.5): рассмотрим вал CD, опирающийся на подшипники B и A и находящийся в равновесии под действием приложенных к нему в сечениях E, K и L моментов. Сделав сечение а - а где-либо на участке DL и рассмотрев равновесие правой отсеченной части, убедимся, что Тк = 0. Если мы сделаем затем сечение b - b в любом месте участка LK, то из условия равновесия правой от сечения части получим Тк = 20 кН * м. Момент считаем положительным в соответствии с принятым правилом знаков. Сделав сечение с - с на участке KE из условия равновесия правой части, получаем 20 - 30 - Тк = 0. Откуда Тк = -10 кН * м.
Получившаяся эпюра имеет форму двух прямоугольников. Важно заметить, что в местах приложения внешних моментов ординаты эпюры скачкообразно изменяюися на величину приложенного здесь внешнего момента. Если заданы поперечные нагрузки, вызывающие кручение стержня (рис. 2.2), то предварительно вычисляют внешние скручивающие моменты, создаваемые этими силами. В случае, представленном на рис. 2.2, внешний скручивающий момент от силы F равен T = Fr. После определения внешних моментов определяют внутренние крутящие моменты и строят эпюры, как указано выше. Напряжение при кручении Вращающийся стержень, работающий на кручение называют 0%92%D0%B0%D0%BB_(%D1%82%D0%B5%D1%85%D0%BD%D0%B8%D0%BA%D0%B0)"валом. Стержень, используемый как упругий элемент, который работает на скручивание, называется 0%A2%D0%BE%D1%80%D1%81%D0%B8%D0%BE%D0%BD"торсионом. Касательные напряжения
где r — расстояние от оси кручения. Очевидно, что касательные напряжения достигают наибольшего значения на поверхности вала при
где Wp — 0%9F%D0%BE%D0%BB%D1%8F%D1%80%D0%BD%D1%8B%D0%B9_%D0%BC%D0%BE%D0%BC%D0%B5%D0%BD%D1%82_%D1%81%D0%BE%D0%BF%D1%80%D0%BE%D1%82%D0%B8%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F&action=edit&redlink=1"полярный момент сопротивления. Это даёт возможность записать условие прочности при кручении в таком виде:
Используя это условие, можно или по известным силовым факторам, которые создают крутящий момент Т, найти полярный момент сопротивления и далее, в зависимости от той или иной формы, найти размеры сечения, или наоборот — зная размеры сечения, можно вычислить наибольшую величину крутящего момента, которую можно допустить в сечении, которое в свою очередь, позволит найти допустимые величины внешних нагрузок.
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 772; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |





 , возникающие в условиях кручения, определяются по формуле:
, возникающие в условиях кручения, определяются по формуле: ,
, и при максимальном крутящем моменте
и при максимальном крутящем моменте  , то есть
, то есть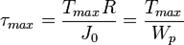 ,
, .
.


