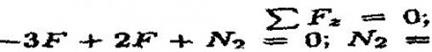Внутненние силы в поперечном сечении

Напряжение полное, нормальное, касательное.

Напряжением называется интенсивность действия внутренних сил в точке тела, то есть, напряжение — это внутреннее усилие, приходящееся на единицу площади. По своей природе напряжение — это поверхностная нагрузка, возникающая на внутренних поверхностях соприкасания частей тела. Напряжение, так же как и интенсивность внешней поверхностной нагрузки, выражается в единицах силы, отнесенных к единице площади:Па=Н/м² (МПа = 10⁶ Н/м², кгс/см²=98 066 Па ≈ 10⁵Па, тс/м² и т. д.).

Рассечем тело произвольным сечением Выделим небольшую площадку ∆A. Внутреннее усилие, действующее на нее, обозначим∆ R . Полное среднее напряжение на этой площадке р =∆ R ∆ A. Найдем предел этого отношения при ∆ A 0. Это и будет полным напряжение на данной площадке (точке) тела.

p =lim A 0 A R

Полное напряжение p , как и равнодействующая внутренних сил, приложенных на элементарной площадке, является векторной величиной и может быть разложено на две составляющие: перпендикулярное к рассматриваемой площадке – нормальное напряжение σ_n и касательное к площадке – касательное напряжение n. Здесь n – нормаль к выделенной площадке1.

Касательное напряжение, в свою очередь, может быть разложено на две составляющие, параллельные координатным осям x, y, связанным с поперечным сечением – nx ny. В названии касательного напряжения первый индекс указывает нормаль к площадке,второй индекс — направление касательного напряжения.

p = n nx nx

Отметим, что в дальнейшем будем иметь дело главным образом не с полным напряжением p , а с его составляющими σ x xy xz. В общем случае на площадке могут возникать два вида напряжений: нормальное σ и касательное τ.

 

Растяжение, сжатие. Продольные силы и их эпюры.

Относительное продольное растяжение (сжатие) твердого тела сопровождается его относительным сужением (расширением) M / d, где d - поперечный размер образца. [ 1 ]

Отношение продольного растяжения р к относительному продольному удлинению 8Х называется коэффициентом Е упругости при растяжении. [ 2 ]

Коэффициент продольного растяжения - величина, обратная модулю Юнга. [ 3 ]

Деформация продольного растяжения или сжатия сопровождается изменением поперечных размеров деформируемого стержня. [ 4 ]

Характеристики продольного растяжения менее чувствительны к прочности связи, чем другие механические свойства. Бэйкер и Крэтчли [2] показали, что для оптимизации усталостных характеристик композита Al - Si02 необходима много более прочная вязь, чем для оптимизации продольных. Проблема оптимизации связи наиболее актуальна, для систем псевдопервого класса, и для полного понимания их поведения многое еще предстоит сделать. [ 5 ]

При продольном растяжении (рис. 5.1) процесс деформации прекращается, когда упругие силы становятся равными растягивающей силе F. [ 6 ]

Растяжение и сжатие

Растяжением или сжатием называют вид нагружения, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор -продольная сила.
Продольные силы меняются по длине бруса. При расчётах после определения величин продольных сил по сечениям строится график - эпюра продольных сил.
Условно назначают знак продольной силы Если продольная сила направлена от сечения, то брус растянут. Растяжение считают положительной деформацией.
Если продольная сила направлена к сечению, то брус сжат. Сжатие считают отрицательной деформацией. Примеры построения эпюр

 

Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплён в стене (закрепление «заделка») (рис. 30.)
Делим брус на участки закрепления.

Участком закрепления считают часть бруса между внешними силами.
На представленном рисунке 3 участка нагружения.
Расчёт начинаем со свободного конца бруса, чтобы не определять величины реакции в опорах.
Участок 1:

 

Продольная сила положительна, участок 1 растянут. Участок 2:

 

=F. Продольная сила положительна, участок 2 растянут.
Участок.'
Продольная сила отрицательна, участок з сжат. Полученное значение равно реакции в заделке.
Под схемой бруса строим эпюру продольной силы (рис.31.).
Эпюра продольной силы строится только под брусом.

 

Эпюрой продольной силы называется график распределения продольной силы вдоль от бруса.
Ось эпюры параллельна продольной оси. Нулевая линия проводится тонкой линией. Значения чисел откладывают от оси, положительные - вверх, отрицательные вниз.
В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz.
Правило контроля: в месте приложения внешней силы на эпюре должен быть скачек на величину приложенной силы.
На эпюре проставляют значения Nz. Величины продольных сил откладывают в заранее выбранном масштабе.
Эпюра по контуру обводится толстой линией и обводится поперёк оси.
Принцип смягчения граничных условий гласит: в точках тела, удалённых от мест нагрузки, модуль внутренних сил мало зависит от способа закрепления. Поэтому при решении задач не уточняют способ закрепления.

Продольное сжатие

Разрушение при продольном сжатии может происходить в различных формах, которые показаны на рис.1:

- микровыпучивание волокон при упругом или пластическом состоянии матрицы;

- микровыпучивание волокон после нарушения адгезионной связи

между ними и матрицей;

- расслаивание;

- выпучивание слоя;

- сдвиговое разрушение слоя;

- разделение слоев из-за поперечного растяжения в направлении

толщины слоя (поперечное расслаивание от растяжения).

Микровыпучивание волокон при упругих напряжениях в матрице возникает в слоях с весьма малой объемной долей волокон. Переход матрицы в пластическое состояние и отслаивание волокон от матрицы возникает, как правило, при объемной доле волокон y? 0,4.

Экспериментальные данные по продольному сжатию показывают, что слой не может выдерживать достаточно высокую сжимающую нагрузку, чтобы достигнуть полной прочности. При разрушении слоя от сжимающей нагрузки напряжение в волокнах значительно меньше их ожидаемой прочности на сжатие.

а – микровыпучивание; б – отслаивание волокна от матрицы;

в – выпучивание слоя; г – сдвиговые разрушения