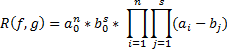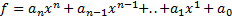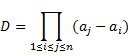Параграф 8. Многочлены над произвольными полями

Пусть р- произвольное числовое поле.

Как известно, над полями R и C всякий многочлен ненулевой степени единственным образом представим в виде разложения на линейные множители. Причем линейные множители могут иметь степень меньшую или равную степени исходного уравнения.

Далее будем рассматривать многочлены ненулевых степеней.

Как известно из свойств делимости многочленов для любого полинома его делителем будут многочлены нулевой степени, то есть числа из поля Р. Из этих же свойств имеет место тот факт, что делителями произвольного многочлена f будут делители вида c*f(x) которые имеют степень равную degF.

Подводя итог сказанному, делителями многочлена являются многочлены нулевой степени или степени равной степени исходного.

Возникает вопрос, имеет ли произвольный многочлен f(X) c Коэффициентами из поля р делители, степени которых больше нуля но меньше степени исходного многочлена?

Ответ: Подобное не всегда имеет место.

Произвольный многочлен f degf=n (>0) с коэффициентами из произвольного числового поля р называется приводимым в поле Р, если его можно представить в виде произведения как минимум двух многочленов, степени которых строго меньше N но больше нуля.

Произвольный многочлен f degf=n (>0) с коэффициентами из произвольного числового поля р называется не приводимым над полем р, если его можно представить в виде произведения как минимум двух многочленов, при этом степень одного из них всегда будет нулевой, а степень другого в точности равна n.

Многочлен f не приводим над полем р, если его нельзя представить в виде произведения многочленов, степени которых отлична от нуля и n.

Основные свойства неприводимых многочленов над полем р:

1) Всякий многочлен первой степени является неприводимым.

2) Если многочлен неприводим над полем р, то и всякий многочлен вида с*f(x) так же будет не приводим.

3) F(x) – произвольный многочлен над р, а g(x) неприводимый многочлен над р, то либо f делится на g, либо они взаимно просты (f так же не приводим)

Кольцо многочленов изоморфно кольцу ценных чисел. В кольце Z важную роль играют простые числа, и их аналогии в кольце многочленов играют неприводимые многочлены.

Теорема Евклида (утрированная):

Всякий многочлен ненулевой степени представим в виде разложения на неприводимые многочлены множители.

Теорема о разложении на неприводимые множители:

Если многочлен f(x) (Степень больше нуля), с коэффициентами из поля р разложим на произведение неприводимых множителей 2-мя способами (и более), то либо количество множителей в произведениях совпадает, либо при соответствующей нумерации делителей множители в этих произведениях пропорциональны.

Примечание:

Произвольный многочлен f Над полем р можно преставать в виде разложения на неприводимые множители не единственным образом.

Понятие простого или кратного корня аналогичны уже имеющимся, а так же и другие термины.

Теорема о разложении на неприводимые множители над полями R и C:

1) Всякий многочлен первой степени над полями R и C является неприводимым

2) Многочлены второй степени над полем R является неприводимым, если его дискриминат отличен от нуля.

3) Всякий многочлен степени большей 1 над полем С является приводимым.

Дополнительные сведения о полиномах:

Пусть f(x) – многочлен ненулевой степени с коэффициентами из некоторого поля р

Одной из важнейших задач считается определение корней многочлена f(x) Над полем р. Если окажется что многочлен не имеет корней над полем р, то существует такое расширение поля Р, содержащее поле Р в котором многочлен имеет корень.

Без потери общности можно считать, что степень рассматриваемого многочлена больше 1. Это дает возможность разложить многочлен на неприводимые множители. Если какой-либо из неприводимых множителей из разложения имеет корень над полем Р, то и сам многочлен f(x) так же будет иметь корень над этим полем.

Теорема(о существовании корня):

Для всякого многочлена f(x), неприводимого над полем Р, существует такое расширение р, в котором полином f(x) имеет корни. Все минимальное расширение поля р, удовлетворяющее первой части теоремы, и (имеющие) содержащие корень многочлена f(x) будут изоморфными.

Следствие из теоремы:

Если лежащий в расширении р корень а многочлена f(x) является так же корнем некоторого многочлена g(x) то многочлен f будет делителем многочлена g.

Расширение Р, в котором многочлен имеет корни, так же называется полем разложения многочлена.

Теорема (о поле разложения):

Всякий многочлен с коэффициентами из поля Р имеет свое поле разложение Р(расширение).

Расширение Р называется полем разложения многочлена, если оно содержит в точности все корни многочлена.

Результат и дискриминант.

Пусть дан многочлен f с коэффициентами из поля р. Если многочлен зависит от нескольких переменных, то такой набор чисел из р, при котором после подстановки их вместо переменных в многочлен f он принимает значение нуля, называется решение многочлена f.

Всякий многочлен имеет решение.

Два многочлена называются взаимно простыми если они не имеют общих решений (или корней)

Два многочлена обладают общим корнем тогда и только тогда, когда они не являются взаимно простыми над некоторым полем Р.

Для решения вопроса о наличии общих корней для двух многочленов вводится понятие результата, который определяется следующим образом.

Теорема о результате:

Два многочлена f(x) и g(x) имеют общий корень тогда и только тогда, когда из результат равен нулю.

Результат двух многочленов может быть представлен в виде полинома выраженного через коэффициенты многочленов f И g или в виде детеминанта порядка n+s.

Он дохуя большой и я его не могу писать.

Пусть дан многочлен

Пусть а1,а2,..,аn. – корни многочлена f(x).

Возникает вопрос, будут ли среди данных чисел равные между собой. Они будут, если величина называемая дискриминантом f(x) будет равна нулю.

Многочлен f будет обладать кратными корнями тогда и только тогда, когда его дискриминант равен нулю, а так же в случае когда многочлен f и его первая производная обладает общими корнями.