
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параграф 1. Базис лвп. Понятие лвп.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть к – произвольное числовое поле. Е – непустое множество n-мерных упорядоченных наборов (векторов). Это так же означает, что n-мерные вектора из множества Е можно умножать на элемент из поля К. А так же рассматривать всевозможные линейные комбинации из поля К. Первое определение линейного пространства: V(k) – непустое множество называется линейным векторным пространством если для n – мерных векторов множества V выполнены аксиомы ЛВП: 1) Свойство замкнутости ЛВП относительно сложения векторов и умножения вектора на число из К
2) Существование нулевого элемента
3) Существование противоположного элемента: Для любого ненулевого вектора
4) Закон сложения и умножения векторов на число a. Коммутативности: b. Ассоциативности: c. Дистрибутивности: 5) Дополнительные законы a. Закон дистрибутивности относительно сложения скаляров:
b. Ассоциативности: c. Операции сложения и умножения на скалярах называются внутренними законами композиции. Второе определение ЛВП: Непустое множество V вместе с определениями сложения и умножения на число называется ЛВП, если выполнено условие. 1) Является абелевой (коммутативной) группой 2) Множество V относительно умножения на число образует моноид (выполнен закон дистрибутивности относительно сложения скаляров)
Пусть Система Е называется системой порождающих если любой вектор из ЛВП V представим в виде линейной комбинации векторов из системы Е
Базисом ЛВП называется множество всех его линейных независимых векторов или множество состоящее из максимального количества всех линейно независимых векторов ЛВП. Лемма о порождающих: Всякое линейное векторное пространство содержит систему порождающих. Доказательство (набросок): Пользуясь определением системы порождающих и тем фактом что ЛВП по определению непустое, будем строить требуемую систему: Произвольным образом выберем ненулевой вектор. С помощью чего рассмотрим нетривиальные линейные комбинации с этим вектором, в результате чего получим некоторое множество векторов порожденных этим вектором. Конечно же, ЛВП этим множеством не ограничивается. Добавим к исходному порождающему вектору другой, который линейно не выражается через данный вектор. Используя полученную систему из 2-х векторов рассмотрим все возможные их нетривиальные линейные комбинации и в результате получим некоторое множество векторов, порожденных векторами исходной системы. Продолжая выше описанный процесс, в итоге получаем некоторую систему векторов, которая окажется системой порождающих. Примечание к Лемме о порождающих: Если из системы порождающих исключить какой – либо вектор являющийся нетривиальной линейной комбинацией других векторов этой системы, то оставшиеся система так же будет системой порождающих. Лемма о базисе: Всякая система порождающих содержит базис. Доказательство: Пользуясь наброском доказательство леммы(о порождающих) и используя вторую лемму о них, можно построить систему векторов, которая будет содержать все линейно независимые вектора ЛВП. Примечание к лемме о базисе: Может оказаться что в системе порождающих подмножество всех линейно независимых векторов исходной системы может и не быть базисом. Если это имеет место, то эту систему дополняем другими линейно независимыми векторами ЛВП до базиса. Если попалась такая система порождающих, то она является системой порождающих линейного подпространства исходного ЛВП. Размерностью линейного векторного пространства называется количество векторов в базисе этого пространства. Теорема о базисах: Линейное векторное пространство содержит бесконечное(множество) количество базисов. Конечно-мерное ЛВП – это множество полиномов одной переменной. Пусть дана система векторов Линейной оболочкой натянутой на систему векторов Теорема о линейных оболочках: Линейная оболочка, натянутая на произвольную конечную систему векторов образует подпространство исходного ЛВП. Следствие: Линейная оболочка совпадает с исходным ЛВП в том случае когда система является базисом ЛВП (натянута на базис) Даны две системы векторов:
Данные две системы называются эквивалентными, если вектора одной системы линейно выражаются через вектора другой и наоборот. Предложение о линейной независимости эквивалентных систем векторов: Если каждая из систем является линейно независимой то они состоят из одинакового количества векторов Примечание(к предложению): Пусть одна из систем является линейно независимой. Тогда количество векторов другой системы не меньше количества векторов в первой системе. Пусть дано Отображение f называется гомоморфизмом, если выполнены следующие условия: 1) Образ суммы векторов равен сумме образов этих векторов
2) Образ произведения вектора на скаляр равен произведению образа вектора на этот же скаляр
3) Образ произвольной линейной комбинации из ЛВП V равен линейной комбинации образов этих векторов с теми же скалярами (эквивалентное условие)
Гомоморфизмами f называется изоморфным, если он является взаимно однозначным соответствием. Если между двумя ЛВП можно установить взаимно однозначное соответствие (изоморфизм), то данные ЛВП называются изоморфными.
Отношение изоморфизма между ЛВП обладают следующими свойствами. 1) Рефлексивность 2) Транзитивность 3) Симметричность Отношение обладающие указанными свойствами называется отношением эквивалентности Теорема об изоморфных ЛВП: Любые два изоморфных ЛВП имеют одинаковую размерность.
Параграф 2. Подпространства Пусть дано ЛВП V Непустое множество v’ называется подпространством ЛВП V если выполнены условия: 1) Сумма любых двух векторов из множества v’ также является вектором этого множества
2) Произведение любого вектора V’ на скаляр(число) так же является вектором данного множества V’
Ядро гомоморфизма Пусть дан гомоморфизм Ядром гомоморфизма f называется множество всех таких векторов из ЛВП V, образом которых является нулевой вектор ЛВП W.
Образ гомоморфизма Образом гомоморфизма f называется множество все нетривиальных векторов ЛВП W являющихся образами ненулевых векторов из ЛВП V:
Теорема о ядре и образе гомоморфизма: Пусть Ядро гомоморфизма f является подпространством ЛВП V
Образ гомоморфизма f является подпространством ЛВП W.
Доказательство: 1) Покажем что ядро гомоморфизма f является подпространство ЛВП V. - Выберем 2 элемента - Проверим выполняются ли понятие подпространства и основные свойства понятия гомоморфизма:
Из равенства (1) видно, что сумма двух векторов из ядра имеет образ нуль –вектора ЛВП W. Это означает что сумма двух векторов принадлежит ядру гомоморфизма (Первое условие определения подпространства.)
Из неравенства (2) следует, что произведение произвольного скаляра на произвольный вектор x из ядра, так же является вектором из ядра (второе условие определения подпространства) 2) Покажем, что образ гомоморфизма f является подпространством ЛВП W - Выберем x’ и y’ из образа f - Проверим выполняется ли понятие подпространства и основные свойства понятия гомоморфизма.
Так как сумма векторов x’ и y’ не является нуль-вектором Доказательство второго свойства гомоморфизма основываются на приведенных выше выкладках. Теорема о простейших свойствах гомоморфизмов: Пусть 1) 2) Теорема о простейших свойствах изомофризма: Пусть 1) Образом любого ненулевого вектора из V является ненулевой вектор из W
2) 3) Образами векторов, образующих линейно независимую систему в ЛВП V, являются векторами их ЛВП W, которые так же образуют линейно независимую систему.
4) Пусть дана произвольная линейно зависимая система векторов из ЛВП V, причем их линейная комбинация (не тривиальная), приравнена к
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 752; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.162.21 (0.009 с.) |





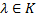


 существует противоположный вектор
существует противоположный вектор






 произвольная совокупность векторов из ЛВП.
произвольная совокупность векторов из ЛВП.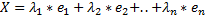




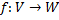 отображающее ЛВП V в ЛВП W.
отображающее ЛВП V в ЛВП W.
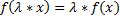



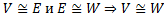

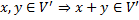

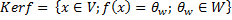
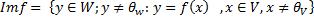


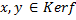
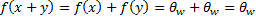 (1)
(1)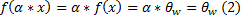
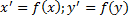
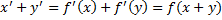
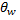 и согласно определению ядра, эта сумма является образом сумы двух ненулевых векторов из ЛВП V.
и согласно определению ядра, эта сумма является образом сумы двух ненулевых векторов из ЛВП V.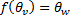

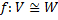 . Имеют место следующие простейшие свойства:
. Имеют место следующие простейшие свойства:
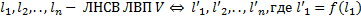 , такие ЛНВС ЛВП W/
, такие ЛНВС ЛВП W/ , с некоторыми скалярами
, с некоторыми скалярами  тогда образом этой системы будет являтся так же линейно зависимая система векторов. При чем нетривиальная линейная комбинация образов приравненная к
тогда образом этой системы будет являтся так же линейно зависимая система векторов. При чем нетривиальная линейная комбинация образов приравненная к 


