Как определить момент инерции маховика по коэффициенту неравномерности хода

Момент инерции маховика, обеспечивающий заданное значение коэффициента неравномерности хода δ, наиболее точно определяется по методу Виттенбауэра или, иначе, по диаграмме «энергия-масса». По данному методу момент инерции для энергетических машин определяется в следующей последовательности

1) Строится зависимость приведённого момента инерции Iп механизма от угла поворота φ звена приведения за цикл установившегося движения. Причём, данный график строится повёрнутым на 90 градусов для удобства использования. 2) Определяется приведённая сила, а по ней затем и приведённый крутящий движущий момент Mпр для всех положений механизма за один цикл установившегося движения и строится график зависимости Mпр(φ) 3) Графическим интегрированием графика Mпр(φ) строится график зависимости работы движущих сил Ад от угла поворота ведущего звена Ад=Ад(φ). Соединяется прямой линией начало и конец полученного графика и получается график зависимости работы сил сопротивления АС за цикл, АС= АС(φ). 4) Строится график изменения кинетической энергии механизма за цикл ΔА = =ΔА(φ). Разность работ ΔА находится по выражению ΔAi=Aдi-Aci. 5) Совместным графическим решением, методом исключения параметра φ графиков Iп=Iп(φ) и ΔA=ΔA(φ)строится график «энергия-масса», т.е. зависимость ΔA=ΔA(Iп)=ΔT1 6) Находятся углы ψmax и ψmin и проводятся касательные под этими углами к графику «энергия-масса». Касательные отсекают на оси ординат отрезок (kl),. 7) Замеряют отрезок (kl) в миллиметрах и подставляя его в формулу для определения момента инерции (IM) маховика, находят момент инерции маховика..

21)Задачи динамич.анализа: 1. Прямая задача динамики (силовой анализ механиз- ма) — по заданному закону движения определить дейст- вующие на его звенья силы, а также реакции в кинемати- ческих парах механизма. 2. Обратная задача динамики — по заданным силам, приложенным к механизму, определить истинный закон движения механизма. В динамический анализ механизмов могут быть включе- ны и задачи уравновешивания и виброзащиты.
22)Задачи динамич.синтеза.: Динамич. синтез механизмов рассматривает задачи создания механизмов и машин. составив прежде всего расчетную формулу для определения приведенного момента инерции I группы звеньев, необходимого для обес- печения заданного значения.
23)Назначение и класс-ция кулчаков.мех-ов: Кулачковые механизмы предназначены для преобразования вращательного движения входного звена в прерывистое, возвратно-поступательное или качательное движение выходного звена. Кулачковые механизмы классифицируются по трём основным признакам. В зависимости от движения выходного звена они могут быть – с поступательным движением; с вращающимся или качающимся выходным звеном, со сложным движением выходного звена. В зависимости от способа замыкания кулачковые механизмы бывают — кинематического или силового замыкания. В зависимости от формы входного звена кулачковые механизмы бывают с плоским или с пространственным кулачком.
24)Силовой анализ кулачкового мех-ма: анализ кулачкового механизма с поступательно действует сила Р21 направленная по нормали п-п. Угол а образован нормалью п-п с направлением движения толкателя 2.Угол а является углом давления. Угол 12 g = 90°— а - угол передачи. Уравнение равновесия толкателя запишется в виде R21 × cosa -T - F = 0 где Т- приведенные в точку В2 сила полезных сопротивлений, сила пружины и сила инерции, F- приведенная сила трения в опоре толкателя. Движение толкателя осуществляется составляющей R21 ¢ = R21 × cosa. А вторая составляющая R21 ¢¢ = R21 ×sin a - вредная и вызывает перекос толкателя и увеличивает силы реакций в его опорах. Поэтому необходимо, чтобы угол а был по возможности меньше.

25)Синтез кулач.мех-ма по допуск.углу давления: Параметры кулачка определяются из кинематических, динамических и конструктивных условий. Кинематические условия обеспечивают заданный закон движения. Динамические, обеспечивают высокий КПД исключают заклинивание, (по допускаемому углу давления). Конструктивные условия выполняют требование прочности. Для кулачковых механизмов с роликовым выходным звеном минимальный радиус кулачка и другие основные размеры (для некоторых схем) определяются по допускаемому углу давления αд.
26)Законы движения выходн-х звеньев.: Необходимый закон движения выходного звена кулачкового механизма достигается за счет придания входному звену (кулачку) соответствующей формы. Кулачок может совершать вращательное, поступательное или сложное движение. Выходное звено, если оно совершает поступательное движение, называют толкателем, а если качательное— коромыслом. Для снижения потерь на трение в высшей кинематической паре применяют дополнительное звено-ролик.Кулачковые механизмы применяются как в рабочих машинах, так и в разного рода командоаппаратах.
27)Критерии синтеза кулач-го мех-ма

Кулачковые механизмы предназначены для преобразования вращательного движения входного звена в прерывистое, возвратно-поступательное или качательное движение выходного звена. Кулачковые механизмы классифицируются по трём основным признакам. В зависимости от движения выходного звена они могут быть – с поступательным движением; с вращающимся или качающимся выходным, со сложным движением выходного звена. В зависимости от способа замыкания кулачковые механизмы бывают — кинематического или силового замыкания. В зависимости от формы входного звена кулачковые механизмы бывают с плоским или с пространственным кулачком. Требования к исходным данным для проектирования. Для проектирования кулачковых механизмов необходимо знать: - кинематическую схему механизма; - закон изменения ускорения ведомого звена в функции обобщенной координаты на различных фазовых углах;некоторые основные параметры (угол давления, эксцентриситет, ход ведомого звена). Параметры кулачка определяются из кинематических, динамических и конструктивных условий. Кинематические условия обеспечивают заданный закон движения. Динамические, обеспечивают высокий КПД исключают заклинивание, (по допускаемому углу давления). Конструктивные условия выполняют требование прочности. Единого универсального критерия, учитывающего весь сложный комплекс вопросов, связанных с выбором закона движения толкателя, не существует. Поэтому при оценке эффективности профиля кулачка устанавливают комплекс заданных условий и ограничений и располагают их в порядке убывающей важности. Наиболее типичным графиком зависимости между перемещением толкателя и углом поворота кулачка является кривая для поступательно перемещающегося толкателя. На этом графике внутри цикла можно выделить четыре фазы и соответствующие им фазовые углы поворота кулачка: угол удаления угол дальнего стояния, угол сближения и угол ближнего стояния. Сумма фазовых углов называется рабочим профильным углом. Иначе это центральный угол, внутри которого расположен рабочий профиль кулачка

Первый этап синтеза - структурный. Структурная схема определяет число звеньев механизма; число, вид и подвижность кинематических пар; число избыточных связей и местных подвижностей. При структурном синтезе необходимо обосновать введение в схему механизма каждой избыточной связи и местной подвижности. Определяющими условиями при выборе структурной схемы являются: заданный вид преобразования движения, расположение осей входного и выходного звеньев. Входное движение в механизме преобразуется в выходное, например, вращательное во вращательное, вращательное в поступательное и т.п. Если оси параллельны, то выбирается плоская схема механизма. При пересекающихся или перекрещивающихся осях необходимо использовать пространственную схему. В кинематических механизмах нагрузки малы, поэтому можно использовать толкатели с заостренным наконечником. В силовых механизмах для повышения долговечности и уменьшения износа в схему механизма вводят ролик или увеличивают приведенный радиус кривизны контактирующих поверхностей высшей пары.

Второй этап синтеза - метрический. На этом этапе определяются основные размеры звеньев механизма, которые обеспечивают заданный закон преобразования движения в механизме или заданную передаточную функцию. Как отмечалось выше, передаточная функция является чисто геометрической характеристикой механизма, а, следовательно, задача метрического синтеза чисто геометрическая задача, независящая от времени или скоростей. Основные критерии, которыми руководствуется проектировщик, при решении задач метрического синтеза: минимизация габаритов, а, следовательно, и массы; минимизация угла давления в вышей паре; получение технологичной формы профиля кулачка.

 

 

28 Профилирование кулачка: При плоском: 1) Проводим окруж-ть кулачка.2)Угол делим на равные участки.3) R равным R=Rsr+ из точки О делаем засечки Rк.4)Из точек с Штрихом проводим перпендикуляр к лучям.5) Проводим внут.огибающую в пределах .Откладываем ост.фазовые углы.в пределах делаем дугу зеркально. При остром: 1.Делим фазы подъема, верхнего выстоя и опускания на диаграмме S=f(φ1)на некоторое количество равных частей. Фазу нижнего выстоя можно не делить. 2.Находим графически значения перемещений толкателя: 3.Радиусом r=r_min проводим окружность и через центр 0 – линию движения толкателя. 4.В соответствии с разметкой углов φ₁ на диаграмме s=f(ϕ1)из центра 0 проводим лучи. Вдоль лучей, начиная от проведенной окружности, откладываем отрезки S₁,S₂,…,S_n. 5.Соединяя полученные точки 1′,2′,…,n ′ плавной кривой получим профиль кулачка. φ_раб = δ_раб = φ_у + φ_дв + φ_с

29)Методика проф.кулачка при роликовом толкателе:1) Проводим окруж-ть кулачка.2)Угол делим на равные участки.3) R равным R=Rsr+ из точки О делаем засечки Rк. надо обвести полученные точки плавной кривой, которая и будет искомым профилем кулачка при угле удаления «j y». Профиль симметричного кулачка на углах «j Д», «j С», «jБ» получается аналогично методике для плоского толкателя.
Только сначала полученный профиль будет являться центровым, то есть перемещение центра ролика. Затем надо в точках пересечения лучей с профилем провести окружности диаметром, равным диаметру ролика. А затем провести внутреннюю огибающую к этим окружностям, которая и будет истинным профилем кулачка. Радиус ролика r следует брать: r» 0,2 Rmin.
30) Допускаемый угол давление в рычажных мех-мах: Как уже отмечалось, при проектировании механизмов нужно учитывать весьма важный параметр, характеризующий условие передачи сил и работоспособность механизма — угол давления ϑ (угол между вектором силы, приложенной к ведомому звену, и вектором скорости точки приложения движущей силы; трение и ускоренное движение масс при этом пока не учитываются). Угол давления не должен превышать допустимого значения: ϑmax ≤ ϑдоп.

1)Что изучает ТММ: Теория механизмов изучает свойства отдельных типовых механизмов, применяемых в самых различных машинах, приборах и устройствах. При этом рассматриваются механизмы как совокупности связанных между собой тел, обладающих различными формами движения. Изучать кинематические и динамические характеристики механизмов в зависимости от их геометрических параметров и действующих на механизмы сил.
2) Звеном в ТММ называется твердое тело, входящее в состав механизма. Под твердым телом в ТММ понимается любая совокупность деталей, не имеющих между собой относительного движения. Кинематической парой называется подвижное соединение двух звеньев. Кинематической цепью называется система звеньев, образующих между собой кинематические пары. Число степеней свободы -это совокупность независимых координат перемещения и/или вращения полностью определяющая положение системы или тела.
3) для плоского механизма имеем: W = 3n-2P5-P4. В механизмах с незамкнутыми кинематическими цепями число подвижных звеньев равно числу кинематических пар и формула: W = P5+2P4+3Р3+4Р2+5P1.
4) Графическое определение кинематических параметров кулачк механизмов. угол удаления φ_y угол дальнего выстоя φ_дв угол сближения φ_с угол ближнего выстоя φ_бв. Сумма трех углов образует угол φ_раб = δ_раб, который называется рабочим углом φ_раб = δ_раб = φ_у + φ_дв + φ_с

5)Определение мин радиуса для плоскгого,качающегося и игольчатого толкателя: Известны: схема механизма, ход толкателя, закон изменения ускорения толкателя S¢¢ = S¢¢(t) или S¢¢ = S¢¢(j), угловая скорость w кулачка, все фазовые углы допускаемый угол a давления. Толкатель – острый. Графическим интегрированием (Рис.8.5.) диаграммы S¢¢ = S¢¢(j) получают диаграммы скорости S¢ = S¢(j) и перемещения S = S(j) толкателя. Затем определяются масштабные коэффициенты полученных диаграмм. Сначала по известному ходу h толкателя определяют масштабный коэффициент оси S по формуле: () y (мм) h м S S max 1 m =, () мм м. Затем определяется масштабный коэффициент оси j по выражению: движущимся толкателем (рис. 8.3.). Без учёта сил трения в точке В2 на толкатель () (0...4), L j y ряд mj =, где j y – угол удаления в радианах, L(0...4)- длина оси j в миллиметрах. Масштабные коэффициенты осей S¢ и S¢¢ определяют по формулам: ×H ¢ = mj m m S S; ×H = ¢ ¢¢ mj m m S S. где H – отрезок в миллиметрах (см. рис.8.5.), постоянная интегрирования. Более подробно методика графического интегрирования изложена в разделе динамического синтеза, при определении момента инерции маховика. Для определения минимального радиуса кулачка 0 Rmin r = необходимо построить зависимость скорости S толкателя от его перемещения S: S¢ = S¢(S), (рис. 8.6.). Для этого на вертикальной оси S откладываем ординаты (1-1¢) y, (2-2¢) y, (3-3¢) y и (4-4¢) y взятые из графика S = S(j) (см. рис. 5). При этом масштабный коэффициент mSR, в котором откладываются эти ординаты, может быть произвольной, или равный mSR = mS Затем, через точки 1¢, 2¢, 3¢, 4¢ (см. рис. 8.6.) проводим горизонтальные линии, перпендикулярные оси S. На этих перпендикулярах откладываем ординаты S i y ¢, взятые из графика S = S(j). Эти ординаты откладывают в масштабе mSR, то есть по осям S и S¢ (должны быть одинаковые масштабные коэффициенты. Затем точки 0, 1¢, 2¢, 3¢, 4¢ обводятся плавной кривой и получается зависимость S¢ = S¢(S), (рис. 8.6.). затем к полученному графику проводится касательная под углом давления a. Эта касательная пересекает ось S в точке В. Расстояние, равное отрезку (ОВ), и будет минимальным радиусом кулачка Rmin, истинная величина которого в метрах равна R (OB) (м) min mSR
6)Профилирование кулачка: При плоском: 1) Проводим окруж-ть кулачка.2)Угол делим на равные участки.3) R равным R=Rsr+ из точки О делаем засечки Rк.4)Из точек с Штрихом проводим перпендикуляр к лучям.5) Проводим внут.огибающую в пределах .Откладываем ост.фазовые углы.в пределах делаем дугу зеркально. При остром: 1.Делим фазы подъема, верхнего выстоя и опускания на диаграмме S=f(φ1)на некоторое количество равных частей. Фазу нижнего выстоя можно не делить. 2.Находим графически значения перемещений толкателя: 3.Радиусом r=r_min проводим окружность и через центр 0 – линию движения толкателя. 4.В соответствии с разметкой углов φ₁ на диаграмме s=f(ϕ1)из центра 0 проводим лучи. Вдоль лучей, начиная от проведенной окружности, откладываем отрезки S₁,S₂,…,S_n. 5.Соединяя полученные точки 1′,2′,…,n ′ плавной кривой получим профиль кулачка. φ_раб = δ_раб = φ_у + φ_дв + φ_с
7)Угол давления в кулачковых механизмах и его влияние на КПД: Надо иметь ввиду, что при вращении кулачка по часовой стрелке, ординаты S i y ¢ откладывают вправо от оси S, а если вращение против часовой стрелки, то влево от оси S. Угол а за оборот принимает различные значения и в одном (на практике а=30°...40° - для поступательных, а=45°...50° - для коромысловых толкателей) положении принимает максимальное значение аmaх. С увеличением угла давления а, уменьшается коэффициент полезного действия, что видно из следующих выражений. 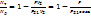Мгновенный КПД h кулачкового механизма без учета трений в высшей паре и в опоре кулачка равен: h=1- (1) где NT - мощность, затрачиваемая на преодоление сил трения в опоре толкателя, NД - мощность движущих сил, F - приведенная сила трения в опоре толкателя, V2 - скорость толкателя. Кулачковый механизм заклинит, если будет выполнено условие: R21 ¢ = R21 × cosa £ F. При заклинивании КПД равен нулю и это будет при угле давления, который называется критическим углом ак. Критический угол давления ак уменьшается с увеличением габаритов механизма. Заклинивает механизм, как правило, на фазе подъема. Поэтому, для устранения заклинивания надо, чтобы угол давления во всех положениях был меньше критического a max < aк. Угол а зависит от величины минимального радиуса 0 r. Чем больше 0 r, тем меньше угол а

8)Динамич.модель мех-ма: Положение механизма с W = 1 вполне определяется од- ной координатой, которая называется обобщенной коор- динатой. В качестве обобщенной координаты чаще всего принимают угловую координату звена, совершающего вра- щательное движение. В этом случае динамическая модель будет (рис. 6.7) представлена в виде: ϕ1 = ϕM — обобщенная угловая координата модели; ω1 = ωM— угловая скорость модели; пр Σ M — суммарный приведенный момент (обобщенная сила — эквивалент всей заданной нагрузки, приложенной к механизму); пр Σ J — суммарный приведенный момент инерции, являю- щийся эквивалентом инерционности механизма.