
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерии выбора типа привода машинСодержание книги Поиск на нашем сайте
Силовой расчёт зуб.передач: При проведении расчета нам необходима информация о размерах зубчатых колес и положении контактной нормали в высшей КП. Для эвольвентной передачи необходимо знать радиусы основных rb1 , rb2 или начальных окружностей rw1 , rw2 и угол зацепления aw, т.к rbi =rw1 × cos aw . По этим размерам в масштабе изображается кинематическая схема механизма, на которую наносятся все известные силы и моменты. Главные вектора и моменты сил инерции рассчитываются по формулам Фi = - mi× aSi, MФi = ISi×ei , так как кинематические параметры aSi, ei механизма при кинетостатическом расчете заданы. Определим подвижность, число избыточных связей в механизме, а также число неизвестных в силовом расчете: Wпл = 3× 2 - 2×2 - 1×1 = 1, qпл = 1 + 0 - 1 = 0, ns = 2×2 + 1×1 + 1 = 6, т.е. в нашем механизме неизвестно 6 компонент реакций, для решения задачи силового расчета необходимо составить 6 уравнений кинетостатики. Структурный анализ механизма показывает, что механизм состоит из одного первичного механизма (звено 1 и стойка) и монады (структурной группы, состоящей из одного звена 2). Анализ начнем со второго звена так, как к нему приложен заданный момент спротивления. 1. Звено 2. Уравнения равновесия для звена 2: векторное уравнение силового равновесия å F = 0; F21 + G2 + F20 = 0; уравнение моментов относительно точки В å MB = 0; Mc2 + MФ2 + F21× rb2 = 0. В начале решается уравнение моментов и определяется величина силы F21. Затем графически в масштабе mF, по векторному уравнению сил строится многоугольник сил (рис.25), из которого определяется величина и направление реакции F20. 2. Звено 1. Расчетная схема для звена 1 приведена на рис. 26. Уравнения равновесия для звена 1: векторное уравнение силового равновесия å F = 0; F12 + G1 + F10 = 0; уравнение моментов относительно точки А å MА = 0; Mc1 - MФ1 + F12× rb1 = 0.
Для звена 1 движущий момент Mд1 рассчитывается по уравнению моментов, а величина и направление реакции F10 определяется графически (рис.27), построением плана сил в масштабе mF. Теорема Жуковского : Если векторы всех сил, приложенных в различных точках звеньев и уравновешенных на механизме, перенести параллельно самим себе в одноименные точки повернутого плана скоростей, то сумма моментов всех указанных сил относительно полюса плана будет равна нулю (повернутый план скоростей- это обыкновенный план, повернутый на 90° в любую сторону) Чтобы найти приведенную массу или приведенный момент инерции надо найти кинетическую энергию всех звеньев механизма и приравнять ее к кинетической энергии звена приведения. Кинетическая энергия звена приведения выражается через приведенную массу mП(кр) либо через приведенный момент инерции () 2 I П кг× м. При плоскопараллельном движении звена его кинетическая энергия находится из выражения:Т= Положение механизма с W = 1 вполне определяется од- ной координатой, которая называется обобщенной коор- динатой. В качестве обобщенной координаты чаще всего принимают угловую координату звена, совершающего вра- щательное движение. В этом случае динамическая модель будет (рис. 6.7) представлена в виде: ϕ1 = ϕM — обобщенная угловая координата модели; ω1 = ωM— угловая скорость модели; пр Σ M — суммарный приведенный момент (обобщенная сила — эквивалент всей заданной нагрузки, приложенной к механизму); пр Σ J — суммарный приведенный момент инерции, являю- щийся эквивалентом инерционности механизма. 18).Неравномерность хода машин: Важной задачей является наивыгоднейшее соотношение сил, масс и скоростей звеньев механизма. Но скорости почти всегда колеблются, что: 1) вызывает дополнительные динамические нагрузки в кинематических парах; 2) понижает КПД машины и её надёжность; 3) могут вызвать значительные упругие колебания в звеньях или машине (потеря прочности и мощности); 4) могут ухудшить тот технологический процесс, который выполняет машина или механизм. Колебания скоростей могут быть периодическими (при установившемся движении) и непериодическими. Регулирование колебаний скоростей при установившемся движении обычно выполняется подбором масс звеньев, которые аккумулируют, а затем отдают энергию. Часто в качестве масс используют маховик. Используют при изучении понятие средней скорости механизма. Методы гашения колебаний Динамические гасители или антивибраторы широко применяются в машинах работающих в установившихся режимах для отстройки от резонансных частот. Динамические гасители могут быть выполнены в виде упругого или физического маятника.Виды: Пружинный одномассный инерционный гаситель, Катковый инерционный динамический гаситель, Маятниковые инерционные динамические гасители, Ударные гасители колебаний, пружинныеударные гасители Силовой расчёт зуб.передач: При проведении расчета нам необходима информация о размерах зубчатых колес и положении контактной нормали в высшей КП. Для эвольвентной передачи необходимо знать радиусы основных rb1 , rb2 или начальных окружностей rw1 , rw2 и угол зацепления aw, т.к rbi =rw1 × cos aw . По этим размерам в масштабе изображается кинематическая схема механизма, на которую наносятся все известные силы и моменты. Главные вектора и моменты сил инерции рассчитываются по формулам Фi = - mi× aSi, MФi = ISi×ei , так как кинематические параметры aSi, ei механизма при кинетостатическом расчете заданы. Определим подвижность, число избыточных связей в механизме, а также число неизвестных в силовом расчете: Wпл = 3× 2 - 2×2 - 1×1 = 1, qпл = 1 + 0 - 1 = 0, ns = 2×2 + 1×1 + 1 = 6, т.е. в нашем механизме неизвестно 6 компонент реакций, для решения задачи силового расчета необходимо составить 6 уравнений кинетостатики. Структурный анализ механизма показывает, что механизм состоит из одного первичного механизма (звено 1 и стойка) и монады (структурной группы, состоящей из одного звена 2). Анализ начнем со второго звена так, как к нему приложен заданный момент спротивления. 1. Звено 2. Уравнения равновесия для звена 2: векторное уравнение силового равновесия å F = 0; F21 + G2 + F20 = 0; уравнение моментов относительно точки В å MB = 0; Mc2 + MФ2 + F21× rb2 = 0. В начале решается уравнение моментов и определяется величина силы F21. Затем графически в масштабе mF, по векторному уравнению сил строится многоугольник сил (рис.25), из которого определяется величина и направление реакции F20. 2. Звено 1. Расчетная схема для звена 1 приведена на рис. 26. Уравнения равновесия для звена 1: векторное уравнение силового равновесия å F = 0; F12 + G1 + F10 = 0; уравнение моментов относительно точки А å MА = 0; Mc1 - MФ1 + F12× rb1 = 0.
Для звена 1 движущий момент Mд1 рассчитывается по уравнению моментов, а величина и направление реакции F10 определяется графически (рис.27), построением плана сил в масштабе mF. критерии выбора типа привода машин Выбор типа привода является частью общей задачи разработки и создания машины новой конструкции. При этом необходимо учитывать 1) назначение механизма или машины, для которой проектируется данный привод; 2) наличия того или иного источника энергии; 4) характер нагрузки на привод; 5) кинематические параметры машины, т. е. необходимые угловые и линейные перемещения, скорости, законы движения исполнительного устройства машины. 6) число точек и точность позиционирования или точность воспроизведения движения машины; 7) режима работы привода и обеспечения соответствующей механической характеристики; 8) физическое состояние объекта, перемещаемого исполнительным устройством машины (твердое, хрупкое, жидкое тело); 9) условия эксплуатации машины и прежде всего характеристики окружающей среды: пожароопасность, загрязнение, температуру, механические воздействия, ресурс, экономичность и другие факторы. 12)Опред.сил по индик.диаграмам ДВС и компресс.: Рассмотрим определение движущей силы по индикаторной диаграмме двухтактного ДВС, (рис. 4.8) Индикаторная диаграмма - это зависимость давления газа в цилиндре от перемещения S поршня. Рабочий цикл происходит за один оборот вала Рис.4.8 Рассмотрим характерные участки индикаторной диаграммы. Участок "ав " — расширение газов и превращение тепловой энергии в механическую работу; Участок "вс " - выброс газов в атмосферу с последующей продувкой цилиндра. В точке "с " этот процесс заканчивается и начинается обратный ход поршня. Участок "се "- обратный ход поршня с изменением давления. В точке "d " продувка заканчивается и начинается сжатие, до точки "е ". В точке "е " происходит воспламенение смеси и далее на участке "еа " идет процесс сгорания смеси. Затем на участке "ав " цикл повторяется. Итак, полный рабочий цикл совершается за 2хода поршня (прямой и обратный), или за один оборот коленчатого вала. Ординаты индикаторной диаграммы в некотором масштабе являются давлением газа на поршень. Тогда: на участке "авс "- действующая сила; на участке "cde "- действие силы на поршень при его обратном ходе, то есть действие уже сил сопротивления. Произведение давления на площадь поршня дает силу. Эта сила приводится к кривошипу (пальцу) и определяется ее величина Рп для каждого из 12-13ти положений механизма. По этой силе определяется крутящий момент по формуле M2д=Pп l, где l - длина кривошипа. Положительные силы действуют при расширении газа (участок "авс "), (вверх от оси абсцисс), отрицательные - для сжатия (ниже оси абсцисс). В качестве примера определим силу Рк, действующую по индикаторной диаграмме на поршень диаметром D в точке " г ". Следовательно, кривая "авс " характеризует изменения движущей силы при расширении газов, а кривая "cde " в том же масштабе дает представление об изменении действующих на поршень сил при обратном его движении, когда они по существу являются силами сопротивления. Зависимость движущих сил от хода поршня Pg = f(S) удобно строить, развернув индикаторную диаграмму так, что положительные силы (ординаты), соответствующие ходу расширения, отложены вверх от оси абсцисс, а отрицательные для хода сжатия - вниз от оси абсцисс. Пример такой зависимости представлен на рисунке 4.9 для центрального кривошипно-шатунного механизма. Расчёт выполнен для значений параметров: Н=78 мм; Рmax = 2 МПа; Д= 72 мм 13)Опред.привел сил и Кр.моментов: Приведенные силы находим по теореме Жуковского, используя повернутый план скоростей, Находим уравновешивающие силы.Составим уравнение Жуковского для определения силы Fy. УР.общего вида: Теорема Жуковского : Если векторы всех сил, приложенных в различных точках звеньев и уравновешенных на механизме, перенести параллельно самим себе в одноименные точки повернутого плана скоростей, то сумма моментов всех указанных сил относительно полюса плана будет равна нулю (повернутый план скоростей- это обыкновенный план, повернутый на 90° в любую сторону) Чтобы найти приведенную массу или приведенный момент инерции надо найти кинетическую энергию всех звеньев механизма и приравнять ее к кинетической энергии звена приведения. Кинетическая энергия звена приведения выражается через приведенную массу mП(кр) либо через приведенный момент инерции () 2 I П кг× м. При плоскопараллельном движении звена его кинетическая энергия находится из выражения:Т= Положение механизма с W = 1 вполне определяется од- ной координатой, которая называется обобщенной коор- динатой. В качестве обобщенной координаты чаще всего принимают угловую координату звена, совершающего вра- щательное движение. В этом случае динамическая модель будет (рис. 6.7) представлена в виде: ϕ1 = ϕM — обобщенная угловая координата модели; ω1 = ωM— угловая скорость модели; пр Σ M — суммарный приведенный момент (обобщенная сила — эквивалент всей заданной нагрузки, приложенной к механизму); пр Σ J — суммарный приведенный момент инерции, являю- щийся эквивалентом инерционности механизма. 18).Неравномерность хода машин: Важной задачей является наивыгоднейшее соотношение сил, масс и скоростей звеньев механизма. Но скорости почти всегда колеблются, что: 1) вызывает дополнительные динамические нагрузки в кинематических парах; 2) понижает КПД машины и её надёжность; 3) могут вызвать значительные упругие колебания в звеньях или машине (потеря прочности и мощности); 4) могут ухудшить тот технологический процесс, который выполняет машина или механизм. Колебания скоростей могут быть периодическими (при установившемся движении) и непериодическими. Регулирование колебаний скоростей при установившемся движении обычно выполняется подбором масс звеньев, которые аккумулируют, а затем отдают энергию. Часто в качестве масс используют маховик. Используют при изучении понятие средней скорости механизма.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.58.68 (0.008 с.) |

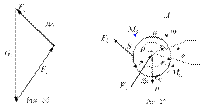
 В выражении первое слагаемое это кинетическая энергия вращательного движения, а второе- поступательного. S- центр тяжести звена. Кинетическая энергия всего механизма равна сумме кинетических энергий всех звеньев: T=å(
В выражении первое слагаемое это кинетическая энергия вращательного движения, а второе- поступательного. S- центр тяжести звена. Кинетическая энергия всего механизма равна сумме кинетических энергий всех звеньев: T=å(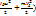 Где n- число подвижных звеньев в механизме. Уравнения кинетической энергии звена приведения, выраженные через массу mП и момент инерции Iп, имеют вид: Т=
Где n- число подвижных звеньев в механизме. Уравнения кинетической энергии звена приведения, выраженные через массу mП и момент инерции Iп, имеют вид: Т=  ; Т=
; Т=  где ν- скорость точки приведения. Iп - приведенный момент инерции относительно оси вращения. Приравняв правые части сначала,а затем получаем приведенную массу mП и приведенный момент инерции IП:
где ν- скорость точки приведения. Iп - приведенный момент инерции относительно оси вращения. Приравняв правые части сначала,а затем получаем приведенную массу mП и приведенный момент инерции IП:  å[I(
å[I( +mi(
+mi(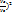 ] Iп=å[Is(
] Iп=å[Is( +mi(
+mi(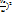 ]
]
 ;
;  ;
;  . Для всего механизма энергия равна: Т = T1+3Т2+ТH. Кинетическая энергия звена приведения равна Т=Iп
. Для всего механизма энергия равна: Т = T1+3Т2+ТH. Кинетическая энергия звена приведения равна Т=Iп  . Приравняв правые части выражений (T) и подставляя в них значения их величин, получаем приведенный момент инерции механизма:
. Приравняв правые части выражений (T) и подставляя в них значения их величин, получаем приведенный момент инерции механизма:  +
+ 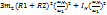
 ,а (Fпр.)= -(Fу.) А Мпр.кр.= -(Fпр.*L1) где L1—длина кривошипа.
,а (Fпр.)= -(Fу.) А Мпр.кр.= -(Fпр.*L1) где L1—длина кривошипа.


