
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механическое движение и его видыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Простейшей формой движения материи является механическое движение – перемещение тел или их частей относительно друг друга. Классическая механика Галилея–Ньютона изучает законы движения макроскопических тел, скорости которых меньше скорости света. Законы движения макроскопических тел со скоростями, близкими к скорости света, изучает релятивистская механика А. Эйнштейна. Квантовая механика изучает движение микроскопических тел – атомов и элементарных частиц. Любое движение твердого тела можно разложить на два основных вида движения – поступательное и вращательное. Поступательным называется движение, при котором любая прямая, жестко связанная с телом, остается параллельной самой себе. При этом все точки тела движутся по одинаковым траекториям. Вращательным называется движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой. Эта прямая называется осью вращения. Тело, относительно которого мы рассматриваем положение других тел в пространстве, называется телом отсчета. С телом отсчета связывается система отсчета – совокупность системы координат и часов. Для описания движения материальной точки и твердого тела наиболее часто используется декартова система координат (рисунок 1).
Рисунок 1 – Определение положения материальной точки
Положение материальной точки в данный момент времени характеризуется тремя координатами x, y и z или радиус-вектором Кинематические характеристики механического движения Поступательное движение Рассмотрим движение материальной точки вдоль произвольной кривой (рисунок 2). Траектория – линия, описываемая материальной точкой при движении в пространстве от точки (1) до точки (2). В зависимости от формы траектории движение бывает прямолинейным или криволинейным.
Рисунок 2 – Определение пути и перемещения Перемещение Путь – сумма длин отрезков траектории от точки (1) до точки (2). При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения равен пройденному пути Δ s.
Для характеристики движения материальной точки вводится векторная величина – скорость, которая определяет быстроту и направление движения. Модуль скорости равен производной пути по времени:
Мгновенная скорость направлена по касательной к траектории. В системе СИ скорость измеряется в м/с. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение:
В системе СИ ускорение измеряется в м/с2. Скорость тела может изменяться как по величине (модулю), так и по направлению. Вектор ускорения принято представлять в виде двух составляющих: тангенциальной и нормальной (рисунок 3). Тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю:
Тангенциальное ускорение направлено по касательной к траектории параллельно вектору скорости в случае ускоренного движения и в противоположную сторону в случае замедленного. Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению. Нормальное ускорение направлено к центру кривизны траектории и численно равно
где R - радиус кривизны траектории в данной точке.
Рисунок 3 – Определение составляющих ускорения (ускоренное движение)
Вектор нормального ускорения и вектор тангенциального ускорения направлены перпендикулярно друг другу. Вектор полного ускорения
Вращательное движение При вращательном движении твердого тела вокруг неподвижной оси все точки тела описывают окружности разных радиусов, центры которых находятся на оси вращения. Все точки тела движутся с разными линейными скоростями и ускорениями и проходят за одно и то же время разные пути. При этом у гол поворота, угловая скорость и угловое ускорение для всех точек тела оказываются одинаковыми (рисунок 4).
Рисунок 4 – Вращение тела вокруг неподвижной оси
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:
где j - угол поворота. Направление угловой скорости определяется по правилу правого винта: если направление вращения тела совпадает с направлением вращения правого винта (буравчика), то направление поступательного движения винта совпадает с направление вектора угловой скорости. В СИ угловая скорость измеряется в рад/с.
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:
В системе СИ угловое ускорение измеряется в рад/с2. Направление вектора углового ускорения определяется по следующему правилу: при ускоренном движении направление углового ускорения совпадает по направлению с направлением угловой скорости, а при замедленном движении направление угловой скорости антипараллельно направлению углового ускорения.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 490; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.147.193 (0.01 с.) |


 , проведенным из начала системы координат в данную точку.
, проведенным из начала системы координат в данную точку.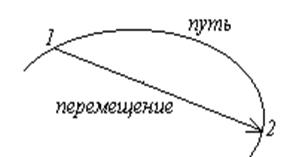
 – вектор, соединяющий начальную (1) и конечную (2) точки траектории, по которой двигалась материальная точка некоторый промежуток времени.
– вектор, соединяющий начальную (1) и конечную (2) точки траектории, по которой двигалась материальная точка некоторый промежуток времени. . (2.1.1)
. (2.1.1)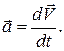 (2.1.2)
(2.1.2) . (2.1.3)
. (2.1.3) , (2.1.4)
, (2.1.4)
 ,
,  , (2.1.5)
, (2.1.5)
 (2.1.6)
(2.1.6) (2.1.7)
(2.1.7)


