
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. Задачі динамічного програмування.
Задача розподілу коштів Нехай існує n стратегій розвитку підприємства. Кожна стратегія вимагає вкладення коштів xj, при прогнозованому прибутку Fj. Знайти оптимальний розподіл коштів С по відповідних стратегіях, який забезпечував би максимальний прибуток. Таблиця 3.1Прогнозовані прибутки реалізації проектів
Коштів можна вкласти не більше с=5. Математичну постановку задачі можна записати наступним чином
xj – сума коштів по кожному проекту Dj – множина варіантів розподілу коштів по j-му проекту. Для розв'язання задачі використаємо метод динамічного програмування. Штучно введемо багатокроковий процес, вважаючи, що на кожному етапі виділяються кошти одному із підприємств. Стан системи Sj на j-му етапі описуємо загальною сумою коштів, розподілених після цього етапу, а управління – сумою коштів хj, виділених для відповідного підприємства. При прийнятті рішення на j-му кроці отримується виграш
При цьому система переходить в стан Sj
Основне функціональне рівняння динамічного програмування визначатиме умовно-оптимальний виграш наступним чином:
Умовно-оптимальний виграш останнього етапу матиме простіший вигляд:
Наступні обчислення для побудови оптимального розподілу коштів зручно оформити у вигляді таблиць. Обчислення починаємо з останнього етапу, знаходячи m=3
m=2
Щоб знайти умовно-оптимальні виграші другого етапу порівнюємо значення W2, які відповідають однаковим станам S1. Ту стрічку якій відповідає максимальне значення умовно-оптимального прибутку позначаємо міткою “V”, якщо таких стрічок є декілька, то їх позначаємо міткою “*”. Для першого етапу аналізуємо лише такі управління, які приводять до початкового стану S0 = 0.
Умовно-оптимальні прибутки цього етапу стають оптимальними, оскільки орієнтуються на дійсний початковий стан. Ланцюжки оптимальних управлінь знаходимо в ході перегляду побудованих таблиць в порядку зростання номерів етапів. Формувати ланцюжки починаємо з оптимальних управлінь першого етапу, які помічені *, або V. (для даної задачі починаємо формувати одразу два ланцюжки). У відповідні таблички заносимо управління та прибутки першого етапу. Для відповідних кінцевих станів першого етапу в попередній табличці вибираємо помічені управління. Якщо ці управління помічені *, то утворюєм відповідну кількість нових ланцюжків з ідентичними управліннями на попередніх етапах. Так в даній задачі утворився третій ланцюжок оптимального управління. Кожен із наведених управлінь (розподілів коштів) забезпечує сумарний прибуток 17.
Метод дає економію в переборі варіантів коли перехід до більшості станів здійснюється за допомогою декількох управлінь. Тобто оптимізація за формулою (3.16) приводить до суттєвого зменшення аналізованих варіантів управлінь, оскільки із багатьох варіантів залишається один або декілька. Це трапляється коли множини варіантів розподілу співпадають для всіх проектів, а їх значення утворені з постійним кроком. Коли в кожний стан веде один шлях, метод зводиться до повного перебору при виконанні обмеження на суму коштів. В таких випадках доцільніше використовувати рекурсивний алгоритм (алгоритм з поверненням).
Рекурсивні алгоритми Формується початковий розподіл коштів одразу по всіх етапах, який потім прагнуть покращити, причому завідомо неоптимальні варіанти виключаються. Початковий план будується за принципом максимального включення: початковим етапам кошти виділяються по максимуму. Якщо при цьому останньому з етапів виділено максимальну кількість коштів, то початковий план – оптимальний. Далі, починаючи з останнього етапу (m), іде поступовий перерозподіл коштів за рахунок попереднього (m-1). З попереднього знімається така кількість коштів, щоби прибуток на останньому етапі збільшувався. Коли кошти попереднього етапу вичерпуються переходять до більш раннього (m-2). При виділенні коштів з етапу m-2 для етапу m-1 кошти знову виділяються за принципом максимального включення. Після цього наступні модифікації починаються із відбирання коштів знову з етапу m-1. При побудові кожного нового варіанту його прибуток порівнюється із найкращим з попередньо досягнутих. При ручних обчисленнях зручно помічати (*) варіанти, які не є оптимальними. Якщо в даному варіанті отримано кращий виграш, то вже він помічається як поточний оптимальний варіант. Алгоритм завершується при неможливості побудови нових варіантів. Варіанти, які на той момент були поточно-оптимальними будуть визначати оптимальні управління даного процесу. Даний алгоритм легко програмується з використанням рекурсивних процедур. Приклад: В умовах попередньої задачі отримаємо наступну послідовність варіантів розподілу, яка приведе до тих же оптимальних розподілів, які отримуються методом динамічного програмування.
Теорія ігор
В багатьох сферах людської діяльності часто зустрічаються проблема прийняття управлінських рішень в умовах невизначеності. Ситуації, в яких ефективність рішення, що приймається однією стороною, залежать від дій іншої сторони, називаються конфліктними. Конфліктна ситуація буде антагоністичною, якщо збільшення виграшу однієї із сторін на деяку величину приведе до зменшення виграшу іншої сторони на таку ж величину. Гра є математичною моделлю реальної конфліктної ситуації, аналіз якої ведеться згідно відповідних правил. В загальному випадку правила визначають послідовність ходів, обсяг інформації кожної сторони про поведінку іншої та результат гри. Якщо в грі беруть участь дві сторони, вона називається парною, а якщо більше – то множинною. Учасники множинної гри можуть утворювати коаліції. Множинна гра перетворюється в парну, коли її учасники утворюють дві постійні коаліції. Сторони, що беруть участь у грі (конфлікті) називаються гравцями. Стратегією гравця є сукупність правил, які визначають вибір варіанту дій при кожному особистому ході гравця в залежності від ситуації, що склалася в грі. В простій одноходовій грі поняття стратегії та вибору ходу гравця співпадають. Гра називається скінченною, якщо число стратегій гравців скінченне і нескінченно, якщо хоча б у одного з гравців число стратегій нескінченне. Стратегія гравця називається оптимальною якщо вона забезпечує даному гравцю при багаторазовому повторенні гри максимально можливий середній виграш або мінімально можливий середній програш, незалежно від поведінки суперника. Вибір однієї з передбачених правилами гри стратегій та її здійснення називають ходом. Ходи бувають особисті та випадкові. В особистому ході гравець свідомо вибирає один із можливих варіантів дій та здійснює його. При випадковому ході вибір відбувається не гравцем а механізмом випадкового вибору. Використовують два способи описання ігор: позиційний та нормальний. Позиційний спосіб пов’язаний зводиться до графа послідовних кроків (дереву гри). Нормальний спосіб полягає представленні стратегій гравців та платіжної функції, яка визначає для кожної сукупності стратегій, що вибрані гравцями, виграш кожної із сторін. Якщо в партії виграш одного з гравців рівний програшу інших, то таку гру прийнято називати грою з нульовою сумою. Для опису парної гри з нульовою сумою використовують платіжну матрицю, елементи якої визначають суму виграшу першого гравця та програшу другого гравця при виборі ними відповідних стратегій. Приклад 1.Побудова платіжної матриці. Розглянемо парну скінченну парну гру з нульвою сумою. Кожен з гравців може записати одну із цифр {1,2,3}. Якщо різниця між очками додатня, то перший гравець виграє різницю, якщо від’ємна, то другий гравець виграє різницю. При рівності очок – нічия. Нижче наведено матрицю описаної гри
Гра 2Х2 без сідлових точок
Нехай гравець А має m а гравець В – n стратегій. Враховуючи, що при відсутності сідлових точок нижня та верхня ціни гри не співпадають (
Стратегії гравців для яких імовірності використання в оптимальних мішаних стратегіях більші нуля, називаються активними. В основній теоремі теорії ігор доводиться, що всяка скінченна парна гра з нульовою сумою має хоча б один розв’язок в мішаних стратегіях. В найпростіших випадках цей розв’язок нескладно знайти аналітично з використанням простого графічного аналізу.
Крім того слід врахувати, що
покладаючи
Прирівнюючи (4.11) та (4.12), отримаємо рівняння відносно р1:
яке при конкретних значеннях коефіцієнтів платіжної матриці розв'язується елементарно. До рівняння (4.14) можна прийти також шляхом простого геометричного аналізу (див.рисунок). Для цього через кінці одиничного відрізка осі абсцис проведемо перпендикуляри, на яких будемо відкладати виграш гравця А при використанні чистих стратегій. Нехай лівому відрізку відповідає стратегія А1, а правому – А2. Відповідно на лівому перпендикулярі будуємо відрізки а11 та а12, а на правому – відрізки а21 та а22. Для побудови відрізка прямої, що відповідатиме результату гри при використанні другим гравцем стратегії В1, проведемо аналіз співвідношень (4.11), (4.13). Рівняння (4.11) визначає пряму, аргументом якої служить p1, а умова (4.13) зводить її до відрізка.
Побудуємо цей відрізок прямої за його крайніми точками. Зокрема в точці А1 p1=1 i Для знаходження оптимального значення
Щоб знайти точне числове значення величини . Оптимальна мішана стратегія гравця В знаходиться аналогічно. Однак відрізки, які будуть відкладатися на вертикалях В1 та В2 повинні відповідати вже результатам гри при цих стратегіях.Гравець В передбачає найбільш несприятливі для себе дії гравця A отримуючи верхню межу програшу – ламану A1NA2, ціну гри Слід відзначити, що розв'язок гри не завжди визначається точкою перетину ліній, що визначають результати гри для певних стратегій. На наступному малюнку показано, коли нижня границя виграшу гравця А співпадає з лінією В2В2.
Стратегія В1 для гравця В явно невигідна, тому гравець А аналізує лише його стратегію В2, вибираючи єдину оптимальну для себе стратегію А2. Отже дана гра має сідлову точку А2В2.Наступний малюнок представляє також випадок наявності сідлової точки, хоча точка перетину оціночних прямих існує. Тут оптимальною є стратегії А1В2
Спрощення ігор
Якщо платіжна матриця гри не містить сідлової точки, то складність розв'язання задачі можна значно знизити, якщо зменшити розмірність платіжної матриці шляхом викреслювання дублюючих та заздалегідь невигідних стратегій. Дублюючим стратегіям відповідають рівні стрічки (стовпчики) платіжної матриці. Якщо всі елементи i-ої стрічки (стовпчика) платіжної матриці не більші відповідних елементів стрічки (стовпчика) j, то стратегія Аі (Вj) називається заздалегідь невигідною. Тема 3. Задачі динамічного програмування.
Динамічне програмування – це математичний метод оптимізації рішень, які приймаються в ході багато етапного процесу з метою оптимізації значення результуючої змінної за весь період управління. Для реалізації цієї мети, управління на кожному кроці повинно враховувати всі наслідки прийнятого рішення для майбутніх періодів. При цьому прийняття рішення на останньому кроці буде найпростішим, оскільки відпаде необхідність враховувати наслідки дій в майбутньому. На цьому кроці можна вибрати оптимальне управління виходячи з умов кроку. Тому процес динамічного програмування починається з останнього етапу і розгортається до першого. Однак, щоби прийняти рішення на останньому етапі (m) потрібно знати результат попереднього етапу (m-1). Оскільки його немає, то потрібно зробити різні допущення щодо стану S процесу управління після завершення попереднього кроку і при кожному із можливих станів вибрати оптимальне управління останнього етапу. Розв'язавши цю задачу, ми знайдемо умовно оптимальне управління на m-тому кроці, тобто управління, яке дозволить прийняти оптимальне рішення при будь-якому можливому стані системи на попередньому кроці. Нехай умовно-оптимальне управління кроку m побудовано. Робимо всеможливі допущення про стан системи після (m-2) кроку і для кожного з них знаходимо таке управління на (m-1) кроці, щоби виграш за останні два кроки був максимальним. Таким чином знаходимо умовно-оптимальне управління для кроку (m-1). Продовжуємо процес, аж до побудови умовно-оптимального управління для першого кроку. Після цього ми можемо знайти оптимальне управління всього процесу. Оскільки нам відомий стан процесу S0 перед його плануванням, то проходячи по кожному етапу від першого до m-го згідно умовно оптимальних управлінь будемо визначати реальні стани оптимального процесу в цілому а також оптимальні управління кожного етапу, які і складуть оптимальне управління всім процесом. Таким чином в процесі оптимізації управління методом динамічного програмування багатокроковий процес проходиться двічі: - перший раз – від кінця до початку, в результаті чого знаходяться умовні оптимальні управління та виграші кожного етапу; - другий раз – від початку до кінця, в результаті чого знаходяться вже дійсні оптимальні управління кожного етапу.
Принцип Беллмана та основне функціональне рівняння динамічного програмування.
В основу поетапної процедури побудови оптимального управління лежить принцип Беллмана: - яким би не був стан системи S системи в результаті певної кількості кроків, управління на найближчому кроці повинно вибиратися так, щоби воно в сукупності з оптимальним управлінням на всіх наступних кроках, приводило до максимального виграшу на всіх наступних кроках, включаючи даний. Позначимо через Нехай ми вибираємо довільне управління
який залежить як від стану системи, так і від вибраного управління. Крім того ми отримаємо деякий виграш на наступних кроках. Згідно принципу оптимальності будемо вважати, що він максимальний. Щоби знайти цей виграш ми повинні знати стан системи перед наступним і+1-им кроком. Цей новий стан буде залежати від стану системи Si-1 та проведеного управління Ui
Виграш, який ми таким чином отримаємо на кроці і буде складати
Однак згідно принципу оптимальності ми повинні вибрати таке управління Ui, при якому величина виграшу на даному кроці буде максимальна
Управління
а рівняння (3.4) називається основним функціональним рівнянням динамічного програмування. Вона дозволяє встановити умовний оптимальний виграш на кроці і, коли цей виграш відомий для кроку і+1. Для останнього кроку потрібно просто максимізувати виграш при всіх допустимих станах системи перед останнім етапом:
Якщо в умові задачі задається область кінцевих станів Se, то оптимізація проводиться не по всіх можливих управліннях
Знаючи умовно оптимальне управління (3.6) на останньому кроці можемо за основним функціональним рівнянням динамічного програмування (3.4) знайти всі умовно-оптимальні виграші та умовно-оптимальні управління до першого кроку
а також побудувати ланцюжок,
який визначатиме це оптимальне управління:
Задача розподілу коштів Нехай існує n стратегій розвитку підприємства. Кожна стратегія вимагає вкладення коштів xj, при прогнозованому прибутку Fj. Знайти оптимальний розподіл коштів С по відповідних стратегіях, який забезпечував би максимальний прибуток. Таблиця 3.1Прогнозовані прибутки реалізації проектів
Коштів можна вкласти не більше с=5. Математичну постановку задачі можна записати наступним чином
xj – сума коштів по кожному проекту Dj – множина варіантів розподілу коштів по j-му проекту. Для розв'язання задачі використаємо метод динамічного програмування. Штучно введемо багатокроковий процес, вважаючи, що на кожному етапі виділяються кошти одному із підприємств. Стан системи Sj на j-му етапі описуємо загальною сумою коштів, розподілених після цього етапу, а управління – сумою коштів хj, виділених для відповідного підприємства. При прийнятті рішення на j-му кроці отримується виграш
При цьому система переходить в стан Sj
Основне функціональне рівняння динамічного програмування визначатиме умовно-оптимальний виграш наступним чином:
Умовно-оптимальний виграш останнього етапу матиме простіший вигляд:
Наступні обчислення для побудови оптимального розподілу коштів зручно оформити у вигляді таблиць. Обчислення починаємо з останнього етапу, знаходячи m=3
m=2
Щоб знайти умовно-оптимальні виграші другого етапу порівнюємо значення W2, які відповідають однаковим станам S1. Ту стрічку якій відповідає максимальне значення умовно-оптимального прибутку позначаємо міткою “V”, якщо таких стрічок є декілька, то їх позначаємо міткою “*”. Для першого етапу аналізуємо лише такі управління, які приводять до початкового стану S0 = 0.
Умовно-оптимальні прибутки цього етапу стають оптимальними, оскільки орієнтуються на дійсний початковий стан. Ланцюжки оптимальних управлінь знаходимо в ході перегляду побудованих таблиць в порядку зростання номерів етапів. Формувати ланцюжки починаємо з оптимальних управлінь першого етапу, які помічені *, або V. (для даної задачі починаємо формувати одразу два ланцюжки). У відповідні таблички заносимо управління та прибутки першого етапу. Для відповідних кінцевих станів першого етапу в попередній табличці вибираємо помічені управління. Якщо ці управління помічені *, то утворюєм відповідну кількість нових ланцюжків з ідентичними управліннями на попередніх етапах. Так в даній задачі утворився третій ланцюжок оптимального управління. Кожен із наведених управлінь (розподілів коштів) забезпечує сумарний прибуток 17.
Метод дає економію в переборі варіантів коли перехід до більшості станів здійснюється за допомогою декількох управлінь. Тобто оптимізація за формулою (3.16) приводить до суттєвого зменшення аналізованих варіантів управлінь, оскільки із багатьох варіантів залишається один або декілька. Це трапляється коли множини варіантів розподілу співпадають для всіх проектів, а їх значення утворені з постійним кроком. Коли в кожний стан веде один шлях, метод зводиться до повного перебору при виконанні обмеження на суму коштів. В таких випадках доцільніше використовувати рекурсивний алгоритм (алгоритм з поверненням).
Рекурсивні алгоритми Формується початковий розподіл коштів одразу по всіх етапах, який потім прагнуть покращити, причому завідомо неоптимальні варіанти виключаються. Початковий план будується за принципом максимального включення: початковим етапам кошти виділяються по максимуму. Якщо при цьому останньому з етапів виділено максимальну кількість коштів, то початковий план – оптимальний. Далі, починаючи з останнього етапу (m), іде поступовий перерозподіл коштів за рахунок попереднього (m-1). З попереднього знімається така кількість коштів, щоби прибуток на останньому етапі збільшувався. Коли кошти попереднього етапу вичерпуються переходять до більш раннього (m-2). При виділенні коштів з етапу m-2 для етапу m-1 кошти знову виділяються за принципом максимального включення. Після цього наступні модифікації починаються із відбирання коштів знову з етапу m-1. При побудові кожного нового варіанту його прибуток порівнюється із найкращим з попередньо досягнутих. При ручних обчисленнях зручно помічати (*) варіанти, які не є оптимальними. Якщо в даному варіанті отримано кращий виграш, то вже він помічається як поточний оптимальний варіант. Алгоритм завершується при неможливості побудови нових варіантів. Варіанти, які на той момент були поточно-оптимальними будуть визначати оптимальні управління даного процесу. Даний алгоритм легко програмується з використанням рекурсивних процедур. Приклад: В умовах попередньої задачі отримаємо наступну послідовність варіантів розподілу, яка приведе до тих же оптимальних розподілів, які отримуються методом динамічного програмування.
Теорія ігор
В багатьох сферах людської діяльності часто зустрічаються проблема прийняття управлінських рішень в умовах невизначеності. Ситуації, в яких ефективність рішення, що приймається однією стороною, залежать від дій іншої сторони, називаються конфліктними. Конфліктна ситуація буде антагоністичною, якщо збільшення виграшу однієї із сторін на деяку величину приведе до зменшення виграшу іншої сторони на таку ж величину. Гра є математичною моделлю реальної конфліктної ситуації, аналіз якої ведеться згідно відповідних правил. В загальному випадку правила визначають послідовність ходів, обсяг інформації кожної сторони про поведінку іншої та результат гри. Якщо в грі беруть участь дві сторони, вона називається парною, а якщо більше – то множинною. Учасники множинної гри можуть утворювати коаліції. Множинна гра перетворюється в парну, коли її учасники утворюють дві постійні коаліції. Сторони, що беруть участь у грі (конфлікті) називаються гравцями. Стратегією гравця є сукупність правил, які визначають вибір варіанту дій при кожному особистому ході гравця в залежності від ситуації, що склалася в грі. В простій одноходовій грі поняття стратегії та вибору ходу гравця співпадають. Гра називається скінченною, якщо число стратегій гравців скінченне і нескінченно, якщо хоча б у одного з гравців число стратегій нескінченне. Стратегія гравця називається оптимальною якщо вона забезпечує даному гравцю при багаторазовому повторенні гри максимально можливий середній виграш або мінімально можливий середній програш, незалежно від поведінки суперника. Вибір однієї з передбачених правилами гри стратегій та її здійснення називають ходом. Ходи бувають особисті та випадкові. В особистому ході гравець свідомо вибирає один із можливих варіантів дій та здійснює його. При випадковому ході вибір відбувається не гравцем а механізмом випадкового вибору. Використовують два способи описання ігор: позиційний та нормальний. Позиційний спосіб пов’язаний зводиться до графа послідовних кроків (дереву гри). Нормальний спосіб полягає представленні стратегій гравців та платіжної функції, яка визначає для кожної сукупності стратегій, що вибрані гравцями, виграш кожної із сторін. Якщо в партії виграш одного з гравців рівний програшу інших, то таку гру прийнято називати грою з нульовою сумою. Для опису парної гри з нульовою сумою використовують платіжну матрицю, елементи якої визначають суму виграшу першого гравця та програшу другого гравця при виборі ними відповідних стратегій. Приклад 1.Побудова платіжної матриці. Розглянемо парну скінченну парну гру з нульвою сумою. Кожен з гравців може записати одну із цифр {1,2,3}. Якщо різниця між очками додатня, то перший гравець виграє різницю, якщо від’ємна, то другий гравець виграє різницю. При рівності очок – нічия. Нижче наведено матрицю описаної гри
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.146.180 (0.01 с.) |
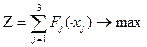 (3.11)
(3.11)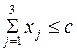 (3.12)
(3.12)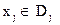 (3.13)
(3.13)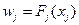 (3.14)
(3.14)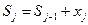 (3.15)
(3.15)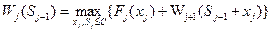 (3.16)
(3.16)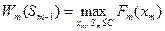 (3.17)
(3.17)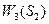 на основі відповідних значень х3 а також таблиці (3.1). Для кожного стану S2 розглядаємо всеможливі розподіли коштів на другому етапі та їх відповідні виграші
на основі відповідних значень х3 а також таблиці (3.1). Для кожного стану S2 розглядаємо всеможливі розподіли коштів на другому етапі та їх відповідні виграші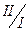
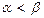 ), природнім є бажання гравця А збільшити свій виграш а гравця В – зменшити програш. Пошук компромісу приводить до використання складної стратегії, яка називається мішаною. Мішані стратегії гравців будемо позначати відповідно
), природнім є бажання гравця А збільшити свій виграш а гравця В – зменшити програш. Пошук компромісу приводить до використання складної стратегії, яка називається мішаною. Мішані стратегії гравців будемо позначати відповідно 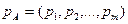 та
та 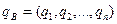 , де pi, qj – імовірності використання чистих стратегій Аі та Вj., причому
, де pi, qj – імовірності використання чистих стратегій Аі та Вj., причому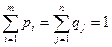 (4.7)
(4.7) Розглянемо найпростіший випадок – гру 2х2 без сідлової точки. Оскільки сідлової точки не існує, то всі стратегії гравців будуть активними. При використанні оптимальної мішаної стратегії гравцем А ціна результат гри буде рівний її ціні при виборі довільної стратегії гравцем В:
Розглянемо найпростіший випадок – гру 2х2 без сідлової точки. Оскільки сідлової точки не існує, то всі стратегії гравців будуть активними. При використанні оптимальної мішаної стратегії гравцем А ціна результат гри буде рівний її ціні при виборі довільної стратегії гравцем В: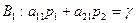 (4.8)
(4.8) (4.9)
(4.9)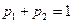 (4.10)
(4.10)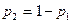 отримуємо
отримуємо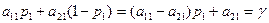 (4.11)
(4.11)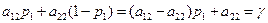 (4.12)
(4.12)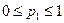 (4.13)
(4.13)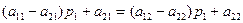 (4.14)
(4.14)
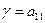 . В точці А2 р1=0 і
. В точці А2 р1=0 і 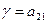 . Оскільки пряма однозначно визначається двома точками, то сполучивши точки (0,а11) і (1,а21), отримаємо графік залежності результату гри при стратегії В1 від імовірності р1. Величина р1 будується на відрізку [0,1] як віддаль поточної точки до точки А2 (віддаль до одиниці). Аналогічно будується пряма для стратегії В2, що сполучає точки (0,а21) і (1,а22).
. Оскільки пряма однозначно визначається двома точками, то сполучивши точки (0,а11) і (1,а21), отримаємо графік залежності результату гри при стратегії В1 від імовірності р1. Величина р1 будується на відрізку [0,1] як віддаль поточної точки до точки А2 (віддаль до одиниці). Аналогічно будується пряма для стратегії В2, що сполучає точки (0,а21) і (1,а22).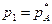 побудуємо нижню границю виграшу гравця І, тобто ломану B2NB1. Із цієї нижньої межі виграшів гравець І прагне вибрати максимальне значення, якому відповідає точка N. Ордината цієї точки рівна ціні гри а абсциса
побудуємо нижню границю виграшу гравця І, тобто ломану B2NB1. Із цієї нижньої межі виграшів гравець І прагне вибрати максимальне значення, якому відповідає точка N. Ордината цієї точки рівна ціні гри а абсциса 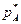 дозволяє знайти параметри оптимальної мішаної стратегії гравця І:
дозволяє знайти параметри оптимальної мішаної стратегії гравця І: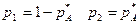 (4.15)
(4.15)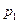 , потрібно розв'язати рівняння (4.14).
, потрібно розв'язати рівняння (4.14).
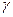 та параметри
та параметри  своєї оптимальної мішаної стратегії.
своєї оптимальної мішаної стратегії.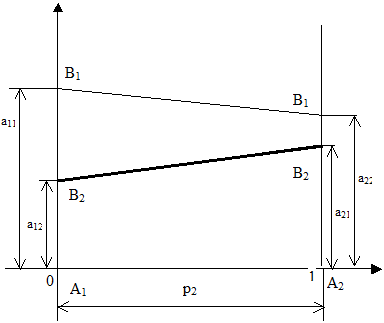

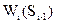 умовний оптимальний виграш, який отримується на всіх наступних кроках починаючи від і-го до останнього. Він рівний максимальному виграшу, який можна отримати на всіх цих кроках разом, якщо перед і-м кроком система перебувала в стані Sі-1. Вважаємо, що цей виграш досягається за допомогою умовно-оптимального управління
умовний оптимальний виграш, який отримується на всіх наступних кроках починаючи від і-го до останнього. Він рівний максимальному виграшу, який можна отримати на всіх цих кроках разом, якщо перед і-м кроком система перебувала в стані Sі-1. Вважаємо, що цей виграш досягається за допомогою умовно-оптимального управління 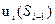 .
.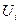 на і-му кроці. При цьому ми отримуємо деякий виграш
на і-му кроці. При цьому ми отримуємо деякий виграш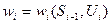 (3.1)
(3.1)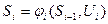 (3.2)
(3.2)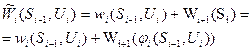 (3.3)
(3.3)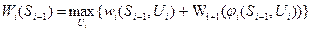 (3.4)
(3.4)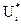 , при якому досягається цей максимум буде умовно-оптимальним управлінням на даному кроці
, при якому досягається цей максимум буде умовно-оптимальним управлінням на даному кроці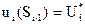 (3.5)
(3.5)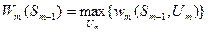 (3.6)
(3.6)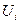 , а лише по тих управліннях
, а лише по тих управліннях 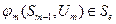 (3.7)
(3.7)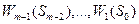 та
та 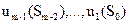 . Оскільки дійсний початковий стан системи
. Оскільки дійсний початковий стан системи 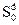 відомий, то можемо знайти оптимальний виграш при управлінні даною системою
відомий, то можемо знайти оптимальний виграш при управлінні даною системою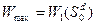 (3.8)
(3.8)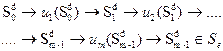 (3.9)
(3.9)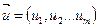 (3.10)
(3.10)


