
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка задачі інтерполяціїСодержание книги
Поиск на нашем сайте
Задача інтерполяції полягає в наступному: на відрізку
Потрібно побудувати функцію Ця задача стає однозначною, якщо замість довільної функції
Геометрично ця задача зводиться до побудови кривої, що збігалася б із заданими значеннями функції у вузлах інтерполяції (рис.2.1). Формули інтерполяції звичайно використовуються для значень При оцінюванні похибки результату повинні враховуватися як похибка методу інтерполяції (залишковий член), так і похибка округлення при обчисленнях. Інтерполяційні формули Ньютона
Інтерполяційні формули Ньютона, як правило, застосовуються для побудови інтерполяційного многочлена у випадку рівновіддалених вузлів, використовуючи горизонтальні таблиці різностей (таблиця 1). Перша інтерполяційна формула Ньютона призначена для інтерполяції й екстраполяції на початку таблиці, тобто в точках, близьких до
де
При
При
Залишковий член визначається за формулою:
де На практиці часто зустрічається потреба для функції, що задана у формі таблиці, підібрати аналітичну формулу, що представляє з деякою точністю задані табличні значення функції. Така формула називається емпіричною. Для побудови емпіричної формули варто враховувати загальні властивості функції. Якщо в таблиці різностей Приклад 2.1. Прийняв шаг Рішення. Побудуємо таблицю кінцевих різностей:
Прийняв
де Підставимо q у рівняння (*), отримаємо:
– емпірична формула для заданої функції.
Друга інтерполяційна формула Ньютона застосовується для інтерполяції та екстраполяції наприкінці таблиці, тобто в точках близьких до
де
Залишковий член визначається за формулою
де
Формула Лагранжа Розглянуті 1-а і 2-а інтерполяційні формули Ньютона придатні лише у випадку рівновіддалених вузлів інтерполяції. Для довільно заданих вузлів інтерполяції використовують інтерполяційну формулу Лагранжа. Побудуємо спочатку поліном
Аналогічно побудуємо поліном
І, нарешті, побудуємо поліном, що приймає в точках
Отримана формула (2.8) називається інтерполяційною формулою Лагранжа. Вона призначена для безпосередньої побудови інтерполяційного многочленна. Коефіцієнти Для обчислення коефіцієнтів Лагранжа може бути використана наведена нижче схема Ейткена. У таблиці
………………………………………………………………
Позначимо добуток елементів першого рядка через
Отже,
Похибка розрахунку має наступний вид:
де Для покращення наближення інтерполяційного полінома до функції Всі інтерполяційні формули виходять з інтерполяційної формули Лагранжа при відповідному виборі вузлів. Приклад 2.2. Для функції побудувати інтерполяційний поліном Лагранжа, вибравши вузли
Рішення. Обчислюємо відповідні значення функції:
Застосовуючи формулу (2.8), отримаємо:
або
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 814; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.163.120 (0.006 с.) |

 задані
задані  точки,
точки,  що називаються вузлами інтерполяції, і значення деякої функції
що називаються вузлами інтерполяції, і значення деякої функції  в цих точках
в цих точках (2.2)
(2.2) ( функція інтерполяції), що приймає у вузлах інтерполяції ті ж значення, що і
( функція інтерполяції), що приймає у вузлах інтерполяції ті ж значення, що і 
 ступеня не вище
ступеня не вище  , тобто такий, що
, тобто такий, що (2.3)
(2.3)
 . Якщо
. Якщо  чи
чи  , то розглядається задача екстраполяції функції.
, то розглядається задача екстраполяції функції. , де
, де  мало по абсолютній величині
мало по абсолютній величині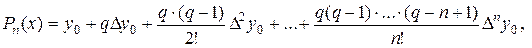 (2.4)
(2.4) – кількість кроків, необхідних для досягнення точки
– кількість кроків, необхідних для досягнення точки 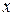 , виходячи з точки
, виходячи з точки 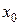 ;
;

 кінцеві різниці (узяті з таблиці 1, підкреслені лінією).
кінцеві різниці (узяті з таблиці 1, підкреслені лінією). одержуємо лінійну інтерполяцію
одержуємо лінійну інтерполяцію
 маємо квадратичну інтерполяцію
маємо квадратичну інтерполяцію .
.
 – точне значення функції.
– точне значення функції.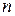 -і різниці функції постійні, то за емпіричну формулу приймають відповідну першу інтерполяційну формулу Ньютона.
-і різниці функції постійні, то за емпіричну формулу приймають відповідну першу інтерполяційну формулу Ньютона. , побудувати на відрізку
, побудувати на відрізку  інтерполяційний поліном Ньютона для функції
інтерполяційний поліном Ньютона для функції  .
.



 ,
,  , маємо:
, маємо: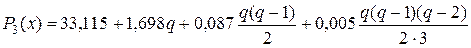 (*),
(*), .
.
 :
: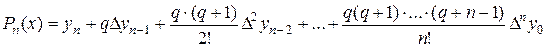 , (2.5)
, (2.5) кількість кроків, необхідних для досягнення точки
кількість кроків, необхідних для досягнення точки  ;
;
 (2.6)
(2.6) , що приймає у точці
, що приймає у точці  значення
значення  , а у решті точок
, а у решті точок  значення
значення 
 .
. , що приймає у точці
, що приймає у точці  значення
значення  , а у решті точок
, а у решті точок  – значення
– значення  :
: . (2.7)
. (2.7) задані значення
задані значення  . Він буде дорівнювати сумі:
. Він буде дорівнювати сумі:

 . (2.8)
. (2.8) в цій формулі називаються коефіцієнтами Лагранжа.
в цій формулі називаються коефіцієнтами Лагранжа. розташовують таким чином:
розташовують таким чином:








 , другого через
, другого через  і т.д. (
і т.д. ( ), а добуток елементів головної діагоналі (елементи підкреслені) через
), а добуток елементів головної діагоналі (елементи підкреслені) через  . Звідки витікає, що
. Звідки витікає, що (2.9)
(2.9)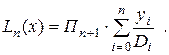
 , (2.10)
, (2.10) – значення інтерполяційного полінома Лагранжа у точці
– значення інтерполяційного полінома Лагранжа у точці  ,
,  ,
,  .
. ,
,  ,
,  .
.




