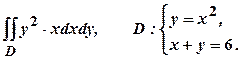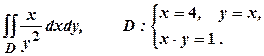Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Властивості подвійного інтегралаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Сталий множник можна винести за знак подвійного інтеграла:
2. Подвійний інтеграл алгебраїчної суми дорівнює відповідній сумі інтегралів від складових:
3. Якщо область інтеграл по всій області
4. Якщо в замкненій області вольняють співвідношення
5. Абсолютна величина інтеграла не перевищує інтеграла від абсолютної величини підінтегральної функції:
6. Теорема про середнє. Якщо замкненій області
де Обчислення подвійного інтеграла в Декартових координатах
Нехай функція
Якщо поміняти місцями
В останній формулі інтегрування ведеться спочатку по Нехай функція
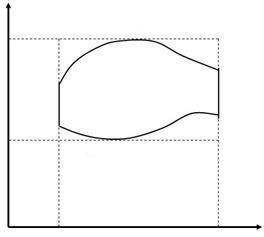
Рис. 1.2 Визначимо у цьому прямокутнику функцію
Функція
Звідси отримаємо наступну формулу:
Якщо область інтегрування
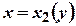
Рис. 1.3
Якщо область ніж у двох точках, то у цьому випадку область
Зразки розв’язування задач
Приклад 1. Обчислити інтеграл
Розв’язання. Шуканий інтеграл дорівнює
Для функції Тому
Шуканий подвійний інтеграл дорівнює:
Приклад 2. Змінити порядок інтегрування у повторному інтегралі
Розв’язання. Побудуємо область інтегрування D, визначивши криві та прямі, якими обмежена ця область (рис. 1.4).
Рис. 1.4 Область
Приклад 3. Обчислити подвійний інтеграл
Рис.1.5 Для обчислення заданого інтеграла краще скористатися формулою (1.3):
Приклад 4. Розставити границі інтегрування двома способами й обчислити подвійний інтеграл
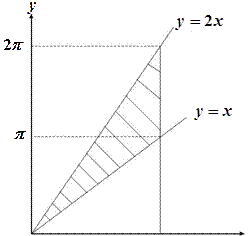
якщо область інтегрування обмежена лініями: Розв’язання. Область інтегрування зображена на рис. 1.6.
Рис. 1.6 Для обчислення заданого інтеграла скористаємось спочатку формулою (1.3.):
Останній інтеграл проінтегруємо за частинами:
Якщо для обчислення даного інтеграла скористатися формулою (1.4), то
Отже, область D треба розбити на дві області, після чого маємо:
тобто ми одержали такий же результат, що й раніше.
Приклад 5. Змінити порядок інтегрування й обчислити повний інтеграл
Розв’язання. Побудуємо область інтегрування D, яка обмежена кривою
Рис 1.7 Спроектуємо область D на вісь Таким чином,
Завдання для самостійної роботи Ι. Змінити порядок інтегрування у повторному інтегралі:
а) б) в) г)
ΙΙ. Обчислити подвійний інтеграл: а) б) в) г)
Обчислення подвійного інтеграла в полярній системі координат.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 631; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.7.115 (0.011 с.) |

 .
.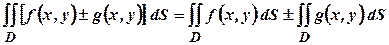 .
. розкласти на скінчене число частин, тоді подвійний
розкласти на скінчене число частин, тоді подвійний .
.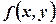 і
і 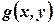 непевні й, задо-
непевні й, задо-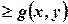 , тоді справедлива нерівність:
, тоді справедлива нерівність: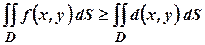 .
.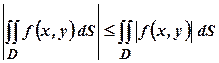 .
.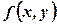 і
і 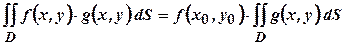 ,
,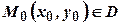 .
.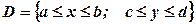 . Вираз
. Вираз 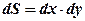 є елементом площі в декартових прямокутних координатах. Подвійний інтеграл від функції
є елементом площі в декартових прямокутних координатах. Подвійний інтеграл від функції 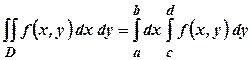 . (1.2)
. (1.2)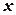 і
і 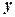 в (1.2), то буде справедливою рівність:
в (1.2), то буде справедливою рівність: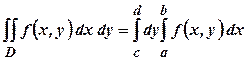 .
.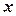 при сталому
при сталому 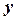 , а потім одержаний результат інтегрується по
, а потім одержаний результат інтегрується по 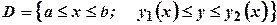 , де
, де 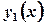 і
і  функції, які неперервні на відрізку
функції, які неперервні на відрізку 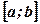 . Візьмемо область
. Візьмемо область 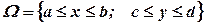 , де
, де 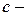 найменше значення
найменше значення 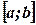 ,
, 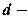 найбільше значення
найбільше значення 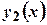 в
в  (рис. 1.2).
(рис. 1.2).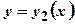
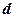
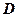
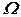
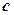

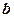
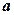
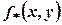 такими рівностями:
такими рівностями: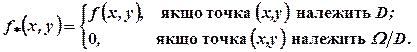
 кусково-неперервна в прямокутнику
кусково-неперервна в прямокутнику  .
.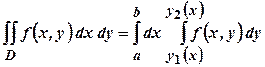 . (1.3)
. (1.3) (рис.1.3), то, змінюючи у формулі (1.3) роль
(рис.1.3), то, змінюючи у формулі (1.3) роль 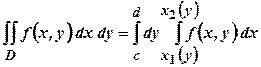 . (1.4)
. (1.4)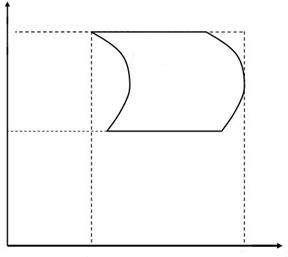
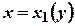

 , якщо область
, якщо область 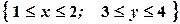 .
.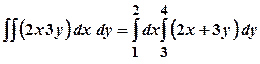 .
. , яка розглядається як функція від
, яка розглядається як функція від 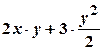 .
.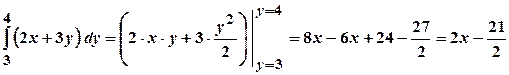 .
.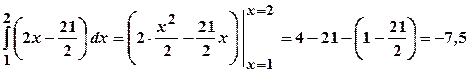 .
.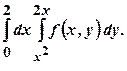
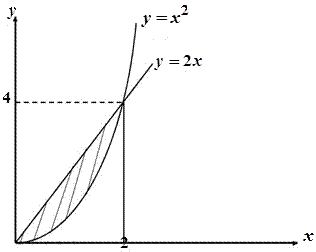
 аналітично має вигляд:
аналітично має вигляд: 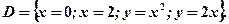 Межі інтегрування вибираємо по змінній
Межі інтегрування вибираємо по змінній 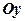 . Область
. Область 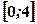 осі
осі 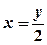 до
до 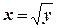 . Таким чином, змінивши порядок інтегрування, матимемо:
. Таким чином, змінивши порядок інтегрування, матимемо: .
.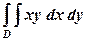 , якщо область
, якщо область 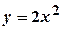 ;
; 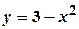 ;
;  .
.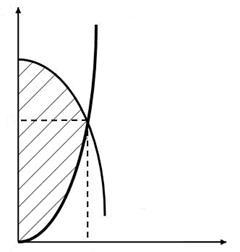 Розв’язання. Область інтегрування зображена на рис. 1.5.
Розв’язання. Область інтегрування зображена на рис. 1.5.

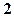
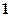

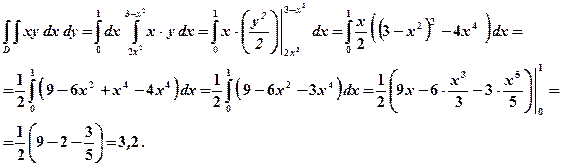
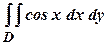 ,
,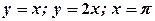 .
.
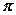
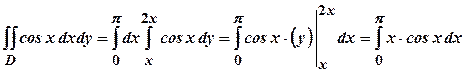 .
.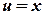 ;
; 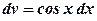 ;
; 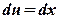 ;
;  . Тоді
. Тоді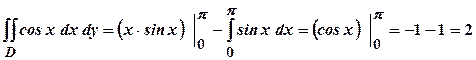 ;
;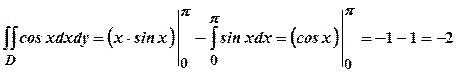 .
.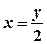 і
і  при
при 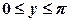 ;
;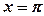 при
при  .
.
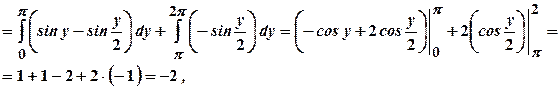
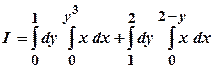 .
.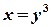 , прямою
, прямою 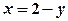 та віссю
та віссю 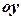 (рис.1.7.).
(рис.1.7.).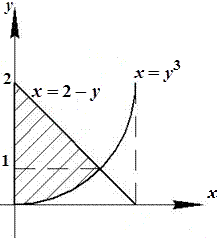
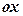 у відрізок
у відрізок 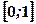 , на якому
, на якому 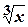 до
до 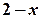 .
.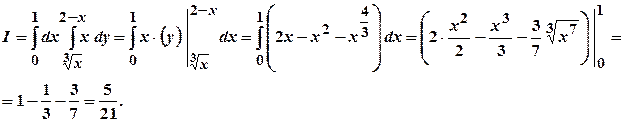
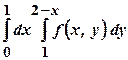 ;
;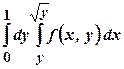 ;
;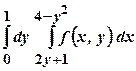 ;
;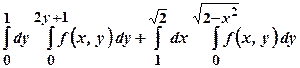 .
.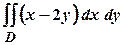 ,
,