
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дослідити на збіжність інтеграли.Содержание книги Поиск на нашем сайте
9.
Підінтегральна функція має на проміжку інтегрування особливу точку Виберемо для порівняння функцію
10.
Підінтегральна функція має особливу точку Виберемо для порівняння функцію
11.
Маємо, що Розглянемо
12.
Підінтегральна функція має особливу точку
Порівняємо функцію правої частини нерівності із функцією
Границя скінченна і дорівнює нулю. Оскільки інтеграл
Завдання для самостійної роботи Дослідити на збіжність (розбіжність) і обчислити інтеграли:
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Дослідити на збіжність інтеграли:
11. 12. 13. 14. Розділ 3 ЗАСТОСУВАННЯ ВИЗНАЧЕНОГО ІНТЕГРАЛА ДО ЗАДАЧ ГЕОМЕТРІЇ Обчислення площ плоских фігур Визначений інтеграл від додатної неперервної функції
В разі, коли


Якщо функція
Площу фігури, обмеженої кривими
У випадку, коли фігура обмежена кривою
Якщо крива задана параметричними рівняннями
де

У полярній системі координат площа криволінійного сектора, обмеженого
Зразки розв’язування задач Обчислити площі фігур, обмежених лініями.
1.
Розв’язання Побудуємо дані лінії і визначимо фігуру, площу якої треба знайти.
Площа визначається за формулою (3.1):
 
2.
Розв’язання Зобразимо фігуру, площу якої шукаємо.
Тоді
3.
Розв’язання Фігура обмежена параболою
Як бачимо, фігура симетрична відносно осі Будемо мати:
4. Розв’язання Побудуємо дані лінії.
5.
Розв’язання Побудуємо параболу
Отже, парабола
6.
Канонічний вид параболи
Парабола симетрична відносно прямої
За формулою (3.4) знайдемо площу:
7. Розв’язання Побудуємо дані гіперболу та пряму.
Отже,
8. Розв’язання Побудуємо дані лінії.
Як бачимо, фігура розташована у I чверті, тому оберемо А саме: де Отримаємо:
Перейдемо до розглядання прикладів обчислення площ у параметричній системі координат для циклоїди та кардіоїди. Обидві ці криві мають механічне походження та описуються точкою кола радіуса
9. Знайти площу фігури обмеженої віссю
Розв’язання Поглянемо на вигляд цієї кривої.
Параметр
Таким чином, площа однієї арки циклоїди втричі більше площі кола, що котиться.
10. Знайти площу, обмежену кардіоїдою
Розв’язання
Наведемо вигляд цієї кривої.
Для обчислення площі використаємо формулу (3.6).
Обчислимо Тоді
Отримаємо:
Тепер ознайомимося із цікавими кривими у полярній системі координат.
11. Обчислити площу, обмежену лемніскатою Бернуллі Розв’язання
Прослідкуємо, як змінюється кут При Таким чином, на чверті площі полярний кут змінюється в межах від
Вся площа
12.Обчислити площу однієї пелюстки рози, яка задається рівнянням Зауваження. Зазначимо, що криві задані рівняннями Щоб знайти площу однієї пелюстки, визначимо, як змінюється полярний кут Нехай При Розв’язання
Повернемось до нашого прикладу: Описуючи площу однієї пелюстки, радіус-вектор пробігає кут від Тоді
13.Обчислити площу, обмежену петлею декартового листа, який визначається рівнянням Розв’язання
Для обчислення площі перейдемо до полярних координат, поклавши Отримаємо:
Так
Винесемо в знаменнику
Зробимо заміну Отже, Ще раз зробимо заміну Тоді:
Отримаємо:
Завдання для самостійної роботи Обчислити площі фігур, обмежених лініями:
1.
2.
3.
4.
5.
6. 7.
8.
9.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 581; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.161.178 (0.01 с.) |

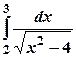 .
. . Розглянемо
. Розглянемо  .
. , інтеграл від якої
, інтеграл від якої  збігається
збігається  . Згідно з ознакою порівняння, заданий інтеграл також збігається.
. Згідно з ознакою порівняння, заданий інтеграл також збігається. .
.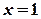 . Розглянемо
. Розглянемо  .
. , інтеграл від якої
, інтеграл від якої  розбігається
розбігається  . Знову застосовуючи ознаку порівняння, робимо висновок, що наш інтеграл також розбігається.
. Знову застосовуючи ознаку порівняння, робимо висновок, що наш інтеграл також розбігається. .
. - особлива точка для підінтегральної функції.
- особлива точка для підінтегральної функції. і оберемо для порівняння функцію
і оберемо для порівняння функцію  . Застосуємо граничну ознаку порівняння, а саме:
. Застосуємо граничну ознаку порівняння, а саме: , а інтеграл
, а інтеграл  збігається
збігається  . Згідно граничній ознаці порівняння,
. Згідно граничній ознаці порівняння,  .
. . Маємо
. Маємо  .
. , після чого застосуємо граничну ознаку порівняння:
, після чого застосуємо граничну ознаку порівняння: .
. збігається
збігається  також збігається. Тоді за ознакою порівняння збігається і інтеграл
також збігається. Тоді за ознакою порівняння збігається і інтеграл  ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;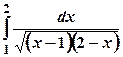 ;
; ;
;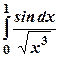 ;
; , заданої на відрізку
, заданої на відрізку  , чисельно дорівнює площі криволінійної трапеції, обмеженої графіком функції
, чисельно дорівнює площі криволінійної трапеції, обмеженої графіком функції  і прямими
і прямими  (рис. 3.1):
(рис. 3.1): . (3.1)
. (3.1) на
на  . (3.2)
. (3.2) .
. та
та  і прямими
і прямими  за умови, що
за умови, що 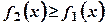 (рис.3.3) знаходять за формулою
(рис.3.3) знаходять за формулою . (3.3)
. (3.3)
 та прямими
та прямими  (рис.3.4), її площу знаходять за формулою
(рис.3.4), її площу знаходять за формулою . (3.4)
. (3.4)
 , де
, де  - неперервні функції, що мають неперервні похідні на відрізку
- неперервні функції, що мають неперервні похідні на відрізку  , то площа криволінійної трапеції, обмеженої цією кривою, прямими
, то площа криволінійної трапеції, обмеженої цією кривою, прямими  та відрізком
та відрізком  , визначається за формулою:
, визначається за формулою: , (3.5)
, (3.5) і
і  - значення параметра
- значення параметра  , при яких
, при яких 
 .
.
 неперервною кривою
неперервною кривою  ,
, та відповідними відрізками променів
та відповідними відрізками променів  (рис. 3.5), дорівнює
(рис. 3.5), дорівнює . (3.6)
. (3.6) .
.
 кв. од.
кв. од. .
.


 кв. од.
кв. од. .
. і прямою
і прямою  .
. Щоб визначити межі інтегрування, знайдемо абсциси точок перетину ліній
Щоб визначити межі інтегрування, знайдемо абсциси точок перетину ліній  , звідки
, звідки  .
. , тому обчислимо площу її правої половини, а загальний результат подвоємо.
, тому обчислимо площу її правої половини, а загальний результат подвоємо. кв. од.
кв. од. .
. Фігура на відрізку
Фігура на відрізку  обмежена зверху
обмежена зверху  , знизу прямою
, знизу прямою  . Її площу знайдемо за формулою (3.3):
. Її площу знайдемо за формулою (3.3): кв. од.
кв. од. .
. . Приведемо рівняння до канонічного виду, виділивши повний квадрат:
. Приведемо рівняння до канонічного виду, виділивши повний квадрат: .
. і перетинає вісь
і перетинає вісь  .
. На відрізку
На відрізку  функція
функція 


 кв. од.
кв. од. .
. :
: тоді
тоді  .
. .
. Точки перетину з віссю
Точки перетину з віссю  , тоді
, тоді , звідки
, звідки ,
,  .
.


 кв. од.
кв. од. .
. Для знаходження абсцис точок перетину графіків розв’яжемо систему рівнянь:
Для знаходження абсцис точок перетину графіків розв’яжемо систему рівнянь: , тоді
, тоді  ,
,  ,
,  , звідки
, звідки  .
.

 кв. од.
кв. од.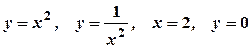 .
. Точки перетину графіків:
Точки перетину графіків: , тоді
, тоді  ,
,  , звідки
, звідки  .
. . На відрізку
. На відрізку  фігура зверху обмежена спочатку графіком функції
фігура зверху обмежена спочатку графіком функції  ), а потім графіком
), а потім графіком  (якщо
(якщо  ). Тому площу всієї фігури знайдемо як суму двох площ, кожну з яких обчислимо за формулою (3.1).
). Тому площу всієї фігури знайдемо як суму двох площ, кожну з яких обчислимо за формулою (3.1). ,
, кв. од.,
кв. од.,  кв. од.
кв. од. кв. од.
кв. од. , що котиться без ковзання по деякій лінії. Для циклоїди цією лінією буде пряма, а для кардіоїди – знов коло радіуса
, що котиться без ковзання по деякій лінії. Для циклоїди цією лінією буде пряма, а для кардіоїди – знов коло радіуса  та однією аркою циклоїди
та однією аркою циклоїди .
.
 до
до  . Використавши формулу (3.5), маємо:
. Використавши формулу (3.5), маємо:


 кв. од.
кв. од. ,
, .
. Крива симетрична відносно осі
Крива симетрична відносно осі  та
та  відповідають значення параметрів
відповідають значення параметрів  .
. :
:  .
.



 .
. кв. од.
кв. од. .
.
 , коли радіус-вектор точки на лемніскаті описує чверть шуканої площі.
, коли радіус-вектор точки на лемніскаті описує чверть шуканої площі. ,
,  . Визна-чимо, чому дорівнює кут
. Визна-чимо, чому дорівнює кут  в рівняння кривої, отримаємо:
в рівняння кривої, отримаємо:  ,
,  ,
,  , звідки
, звідки  .
. . Тоді за формулою (3.6):
. Тоді за формулою (3.6): .
. кв. од.
кв. од. .
. (або
(або  ), де
), де  - постійні величини, називаються розами. Якщо
- постійні величини, називаються розами. Якщо  - пелюсток, якщо
- пелюсток, якщо  , звідки
, звідки  .
. , при
, при 
 . Тобто кут
. Тобто кут  .
.
 - 3-х пелюсткова роза.
- 3-х пелюсткова роза.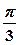 .
.

 кв. од.
кв. од. .
. ,
,  .
.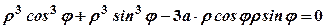 ,
, ,
, .
. як при заміні
як при заміні  на
на  , а
, а  . Тому шукану площу можна розглядати як подвоєну площу
. Тому шукану площу можна розглядати як подвоєну площу  . При цьому радіус-вектор
. При цьому радіус-вектор  повертається від початкового положення
повертається від початкового положення 
 .
. за дужки:
за дужки:
 .
. ,
,  . Нові межі інтегрування:
. Нові межі інтегрування:  ,
,  .
. .
.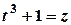 ,
,  ,
,  ,
,  .
. .
. кв. од.
кв. од. ,
,  ;
; ,
,  ,
,  ;
; ,
,  ;
; ,
,  ,
,  ,
, 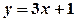 ,
,  ;
;

 ,
,  ;
; .
.


