
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обчислення довжини дуги плоскої кривоїСодержание книги Поиск на нашем сайте
Нехай крива задана рівнянням
Вираз
У разі параметричного задання кривої
Якщо ж гладка крива задана рівнянням
Зразки розв’язування задач 1. Знайти довжину кола.
Розв’язання
Візьмемо коло радіуса
Щоб використати формулу (3.7) знайдемо
Знайдемо довжину чверті кола, що лежить в першій координатній чверті. Обчислимо вираз Маємо: Абсциса Розв’яжемо цю ж задачу, якщо коло задано параметричними рівняннями:
Щоб застосувати формулу (3.9) обчислимо
На всьому колі параметр
Ще більш простим буде розв’язування цієї задачі, якщо рівняння кола задати у полярних координатах. Покладемо Полярна вісь співпадає з додатнім напрямком осі
2. Знайти довжину ланцюгової лінії
Розв’язання Знайдемо
Обчислимо:
3. Знайти довжину дуги лінії
Розв’язання Застосуємо формулу (3.8):
Отже,
(Модуль знято тому, що
4. Обчислити довжину дуги кривої
Розв’язання Застосуємо формулу (3.7): Тоді Отримаємо:
5. Знайти довжину астроїди
Розв’язання
Наведемо вигляд цієї кривої. Користуючись симетрією, обчислимо довжину дуги, що розташована у першій чверті. Вона становитиме чверть від всієї довжини дуги. З рівняння дістанемо:
Піднесемо обидві частини рівності до степеня Тоді Обчислимо Маємо: Тоді
6. Знайти довжину однієї арки циклоїди
Розв’язання
Згадаємо приклад 9 попереднього параграфа: параметр Застосуємо формулу (3.9): Обчислимо
Тоді Тобто довжина однієї арки циклоїди у вісім разів більше радіуса кола, яке її утворює.
7. Знайти довжину дуги кривої
Розв’язання Знайдемо
Тоді
Тоді 8. Визначити довжину всієї кривої Штейнера
Розв’язання
Якщо
Будемо мати:
Маємо: Отже,
9. Знайти довжину кардіоїди
Розв’язання
Для використання формули (3.10) обчислимо Маємо: тоді
У той час, коли точка на кардіоїді пробігає всю криву, її полярний кут змінюється від
10. Знайти довжину дуги кривої
Довжину дуги обчислимо за формулою (3.10). Для цього знайдемо диференціал дуги Маємо:
Тоді
Визначимо, як змінюється полярний кут, коли точка, що рухається по кривій, пробігає її всю. Нехай При Отже,
11. Знайти довжину дуги першого витка спіралі Архімеда
Обчислимо
Тоді
Обчислимо інтеграл: =
Тобто отримали:
Маємо:
Завдання для самостійної роботи Обчислити довжини дуг ліній:
1. 2. 3.
4. 5.
6. 7. Обчислення об’ємів тіл обертання Нехай функція Об’єм тіла, яке утворюється при обертанні навколо осі трапеції, обмеженої кривою
Якщо задані дві неперервні криві
 
У разі параметричного задання кривої рівняннями
 , де , де 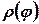 - неперервна функція при - неперервна функція при  . Тоді об’єм тіла, утвореного обертанням навколо полярної осі плоскої фігури, обмеженої кривою . Тоді об’єм тіла, утвореного обертанням навколо полярної осі плоскої фігури, обмеженої кривою  та двома полярними радіусами та двома полярними радіусами  і і  , які відповідають кутам , які відповідають кутам 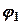 та та  (рис.3.9), обчислюється за формулою (рис.3.9), обчислюється за формулою
Зразки розв’язування задач 1. Знайти об’єм кулі.
Розв’язання
Нехай куля утворена обертанням навколо осі Для обчислення використаємо формулу (3.11), враховуючи, що
Отже,
2. Обчислити об’єм тіла, утвореного обертанням навколо осі
Розв’язання Скористаємось формулою (3.12):
=
3. Знайти об’єм тіла, утвореного обертанням навколо осі Розв’язання
Рівняння Щоб знайти межі інтегрування, шукаємо ординати точок перетину ліній:
Зважаючи на симетрію тіла відносно осі
В завданнях 4 – 7 обчислити об’єми тіл, утворених обертанням навколо осі
4.
Розв’язання Знайдемо межі інтегрування:
За формулою (3.12):
5.
Розв’язання
Знайдемо точки перетину графіків функцій Наша парабола Так як на відрізках
Тоді
6.
Розв’язання РHjpdH
 та пряму та пряму  . Вони перетинаються в точці: . Вони перетинаються в точці:
Пряма Вітка параболи з віссю Знайдемо об’єм тіла як різницю між об’ємами
Маємо:
7.
Розв’язання
Для обчислення об’єму скористаємось формулою (3.14). Знайдемо
8. Знайти об’єм тіла, утвореного обертанням однієї арки циклоїди
Розв’язання
Знайдемо Тоді
Обчислимо останній інтеграл:
Отже,
9. Обчислити об’єм тіла, отриманого обертанням кривої Розв’язання
Рівняння
Завдання для самостійної роботи Обчислити об’єми тіл, утворених обертанням плоских фігур навколо координатних осей:
1.
2.
3.
4.
5.
6. Знайти об’єм тіла, утвореного обертанням кривої
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1536; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |

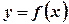 ,
,  , причому
, причому  неперервна разом із своєю похідною на
неперервна разом із своєю похідною на  . Тоді довжина дуги кривої визначається формулою
. Тоді довжина дуги кривої визначається формулою . (3.7)
. (3.7) називається диференціалом дуги. В разі, коли крива задається рівнянням
називається диференціалом дуги. В разі, коли крива задається рівнянням  довжина дуги кривої обчислюється так:
довжина дуги кривої обчислюється так: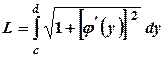 . (3.8)
. (3.8) , довжина дуги дорівнює:
, довжина дуги дорівнює: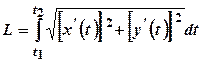 . (3.9)
. (3.9) в полярних координатах, то
в полярних координатах, то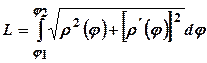 . (3.10)
. (3.10) з центром в початку координат. Його рівняння
з центром в початку координат. Його рівняння  .
. . Знак плюс відповідає верхній половині кола, знак мінус – нижній.
. Знак плюс відповідає верхній половині кола, знак мінус – нижній.
 .
. ,
,  , тоді
, тоді  , тобто
, тобто 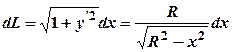 .
. точки кола в першій чверті змінюється від
точки кола в першій чверті змінюється від  до
до  . Довжина кола
. Довжина кола  .
.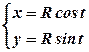 .
. .
. .
. змінюється від
змінюється від  . Тому
. Тому .
. ,
,  . Рівняння кола:
. Рівняння кола:  ,
,  , тобто
, тобто  , звідки
, звідки  .
. , а полярний кут
, а полярний кут  , коли точка пробігає все коло, змінюється від
, коли точка пробігає все коло, змінюється від 
 між точками з абсцисами
між точками з абсцисами  і
і  .
. , тоді
, тоді 

 .
. . За формулою (3.7):
. За формулою (3.7): 
 .
. від точки
від точки  до
до  .
. , тоді
, тоді 
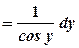 .
.
 .
. - кут першої чверті і
- кут першої чверті і  ).
). від точки
від точки  до
до 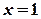 (
( ).
). ,
,  .
. .
.
 .
. .
.
 .
. 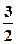 . Отримаємо:
. Отримаємо:  .
. .
.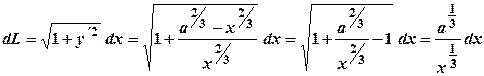 .
. .
. .
. .
. ,
,  .
.
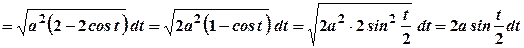 .
.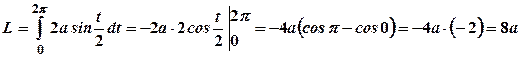 .
. ,
,  від
від  до
до  .
. :
:  ,
, .
.


 .
. .
.
 , рухоме коло описує третину всієї кривої. Знайдемо
, рухоме коло описує третину всієї кривої. Знайдемо  ,
, .
.


 .
.
 .
. .
. .
. Наведемо вигляд цієї кривої.
Наведемо вигляд цієї кривої. та
та 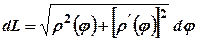 .
. ,
,  ,
,

 .
.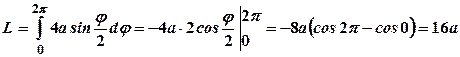 .
.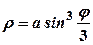 .
. Розв’язання
Розв’язання
 .
.
 .
. , тоді
, тоді  , звідки
, звідки  .
. , при
, при 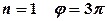 .
.
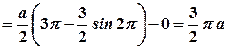 .
. .
. Розв’язання
Розв’язання , тоді
, тоді 
 , де
, де  .
. .
.

 .
. , звідки
, звідки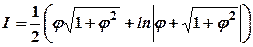 .
.
 .
. 
 від
від  ;
; ,
,  ;
; ,
, 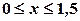 ;
;

 ,
,  ,
,  (рис.3.6), дорівнює
(рис.3.6), дорівнює . (3.11)
. (3.11) такі, що
такі, що  ,
,  при
при 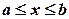 , то об’єм тіла, отриманого обертанням навколо осі
, то об’єм тіла, отриманого обертанням навколо осі  (рис.3.7), обчислюється за формулою
(рис.3.7), обчислюється за формулою . (3.12)
. (3.12) Об’єм тіла, утвореного обертанням навколо осі
Об’єм тіла, утвореного обертанням навколо осі  криволінійної трапеції, обмеженої неперервною кривою
криволінійної трапеції, обмеженої неперервною кривою  , прямою
, прямою  ,
, 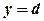 (рис.3.8), дорівнює
(рис.3.8), дорівнює . (3.13)
. (3.13) ,
,  , об’єми утворених тіл обертання навколо осі
, об’єми утворених тіл обертання навколо осі  , (3.14)
, (3.14) . (3.15)
. (3.15)
 . (3.16)
. (3.16) .
. .
.



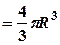 куб. од.
куб. од. ,
,  ,
,  ,
, 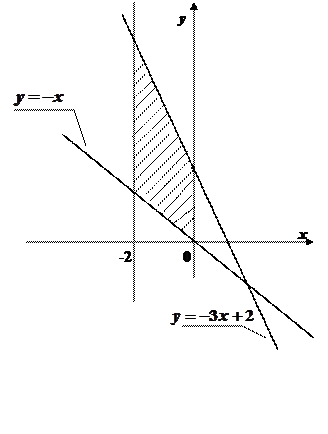





 куб. од.
куб. од. та
та  , віссю симетрії якої є вісь
, віссю симетрії якої є вісь  , тоді
, тоді  , звідки
, звідки  ,
,  .
.
 , за формулою (3.13) маємо:
, за формулою (3.13) маємо:


 куб. од.
куб. од. ,
,  ,
,  , тоді
, тоді  , тоді
, тоді  , звідки
, звідки  . При
. При  маємо
маємо  .
.


 куб. од.
куб. од. ,
,  ,
,  Зобразимо фігуру, при обертанні якої утворюється шукане тіло.
Зобразимо фігуру, при обертанні якої утворюється шукане тіло. , звідки
, звідки  ,
,  . Знайдемо
. Знайдемо  .
. .
. та
та  фігура обмежена різними лініями, то об’єм тіла знайдемо як суму об’ємів
фігура обмежена різними лініями, то об’єм тіла знайдемо як суму об’ємів  , де
, де
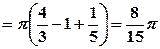 ,
,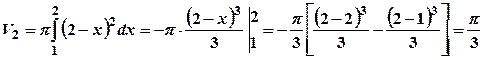 .
. куб. од.
куб. од.



 ,
, 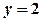 .
. перетинає вісь
перетинає вісь  .
. - об’ємом тіла, утвореного обертанням гілки параболи, та
- об’ємом тіла, утвореного обертанням гілки параболи, та  - об’ємом конуса, утвореного обертанням прямої.
- об’ємом конуса, утвореного обертанням прямої.

 куб. од.
куб. од.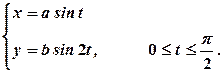
 . Тоді
. Тоді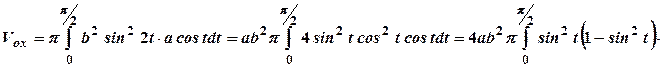

 куб. од.
куб. од.

 .
.
 .
.

 куб. од.
куб. од. навколо полярної осі.
навколо полярної осі. з центром у точці
з центром у точці  . Зрозуміло, що
. Зрозуміло, що  .
.  Для обчислення об’єму використаємо формулу (3.16). Будемо мати:
Для обчислення об’єму використаємо формулу (3.16). Будемо мати: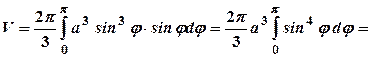

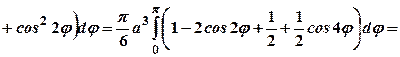
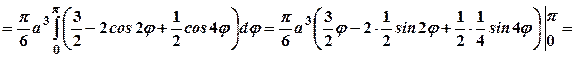
 куб. од.
куб. од. ,
,  ,
,  ?
? ,
,  ,
, 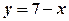 ,
,  ?
?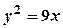 ,
,  ,
, 
 навколо полярної осі
навколо полярної осі 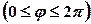 .
.


