
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обчислення площі поверхні тіл обертанняСодержание книги Поиск на нашем сайте
Площа поверхні, утвореної обертанням навколо осі
Якщо гладка крива задана рівнянням
У разі параметричного задання кривої рівняннями
Площа поверхні, отриманої обертанням навколо полярної осі криволінійного сектора, обмеженого неперервною кривою
Зразки розв’язування задач 1. Знайти площу поверхні сфери, як тіла обертання.
Розв’язання
Нехай сфера утворена обертанням кола
Обчислимо
Отже, за формулою (3.17):
Площа поверхні сфери дорівнює
2. Знайти бічну поверхню параболоїда, утвореного обертанням параболи Розв’язання Якщо
Тепер Маємо:
3. Знайти площу поверхні, утвореної обертанням навколо осі Розв’язання
Скористуємось формулою (3.17). Спочатку знайдемо
Отже,
Позначимо
Звідки Повернемося до обчислення площі поверхні:
4. Знайти площу поверхні, отриманої обертанням прямої Розв’язання Виразимо
5. Обчислити поверхню тора, утвореного обертанням кола Розв’язання
Поверхня тора дорівнює сумі поверхонь, утворених обертанням дуг
Для дуги Обчислимо Отже,
Відрізок інтегрування симетричний, тобто
6. Знайти площу поверхні, утвореної обертанням навколо осі Розв’язання Застосуємо формулу (3.19), для цього знайдемо
Тоді отримаємо:
7. Знайти поверхню тіла, утвореного обертанням однієї арки циклоїди Розв’язання
Використовуючи формулу (3.19), обчислимо спочатку Тоді
Отже,
8. Знайти площу поверхні, утвореної обертанням кардіоїди
Розв’язання Використаємо формулу (3.21), для цього знайдемо:
9. Обчислити площу поверхні тіла, утвореного обертанням лемніскати Розв’язання
Тоді Обчислимо
Тоді
Завдання для самостійної роботи Обчислити площі поверхонь тіл, утворених обертанням кривих навколо відповідної осі:
1.
2.
3.
4.
5. Знайти поверхню сфери, заданої в полярних координатах.
Л І Т Е Р А Т У Р А 1. Дубовик В.П., Юрик І.І. Вища математика: Навч. посібник. – К.: А.С.К., 2001. 2. Овчинников П.П. та інші. Вища математика: Підручник. У 2 ч. – К.: Техніка, 2004. 3. Шипачёв В.С. Высшая математика: Учебник для вузов. – М.: Высшая школа, 1998. 4. Шкіль М.І., Колесник Т.В. Вища математика. У 3-х кн.. – К: Либідь, 1994. 5. Вища математика: Збірник задач: Навчальний посібник / За ред. В.П. Дубовика, І.І. Юрика. – К.: А.С.К., 2004. 6. Шипачёв В.С. Задачник по высшей математике: Учебное пособие для вузов.- М.: Высшая школа, 2002. 7. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч.: Учебное пособие для вузов. – М.: Высшая школа, 2000.
Навчальне видання
Кадильникова Тетяна Михайлівна Шинковська Iрина Леонідівна Заєць Iрина Петрівна Запорожченко Олена Євгенівна
ВИЩА МАТЕМАТИКА В ПРИКЛАДАХ ТА ЗАДАЧАХ Частина III Навчальний посібник
Тем. план 2010, поз.251
Підписано до друку 27.10.2010. Формат 60x84 1/16 Папір друк. Друк плоский. Облік.-вид.арк. 4,94. Умов. друк. арк.4,88. Тираж 100 пр. Замовлення №.
Національна металургійна академія України 49600, м. Дніпропетровськ – 5, пр. Гагаріна, 4 ____________________________________________ Редакційно-видавничий відділ НМетАУ
|
||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1193; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.161.43 (0.009 с.) |

 дуги гладкої кривої, заданої функцією
дуги гладкої кривої, заданої функцією 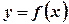 ,
, 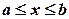 , обчислюється за формулою
, обчислюється за формулою . (3.17)
. (3.17) ,
,  , то площа поверхні, утвореної обертанням кривої навколо осі
, то площа поверхні, утвореної обертанням кривої навколо осі  , може бути обчислена за формулою
, може бути обчислена за формулою . (3.18)
. (3.18) ,
,  ,
,  , де функції
, де функції  ,
,  - неперервні разом із своїми похідними, відповідні площі поверхні обчислюються за формулами:
- неперервні разом із своїми похідними, відповідні площі поверхні обчислюються за формулами: , (3.19)
, (3.19) . (3.20)
. (3.20) та двома полярними радіусами
та двома полярними радіусами  ,
,  , визначається за формулою
, визначається за формулою . (3.21)
. (3.21) навколо осі
навколо осі  :
: (верхня половина кола), тоді
(верхня половина кола), тоді 
 .
. , тоді
, тоді .
. .
. .
. навколо осі
навколо осі  на відрізку
на відрізку  .
.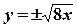 .
. Так як вітки параболи симетричні відносно осі
Так як вітки параболи симетричні відносно осі  . Отже,
. Отже, 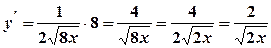 . Тоді
. Тоді  .
.
 .
.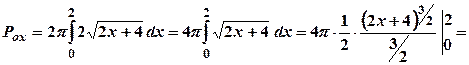

 кв. од.
кв. од.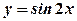 від
від  до
до  .
.

 , тоді
, тоді  .
.

 .
. та обчислимо його частинами. Будемо мати:
та обчислимо його частинами. Будемо мати:
 .
.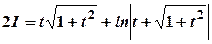 , тому
, тому  .
.

 кв. од.
кв. од. навколо осі
навколо осі  від
від  до
до 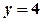 .
. :
:  . Скористаємось формулою (3.18), для цього знайдемо
. Скористаємось формулою (3.18), для цього знайдемо  , тоді
, тоді  .
. Отримаємо:
Отримаємо: 

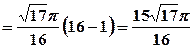 кв. од.
кв. од. навколо осі
навколо осі 

 та
та  навколо осі
навколо осі  , звідки
, звідки  ,
,  .
.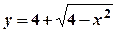 ,
,  ,
,  .
. ,
,  . Для дуги
. Для дуги  ,
,  ,
, 
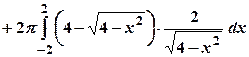 .
.
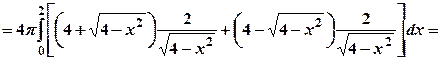

 кв. од.
кв. од.
 ,
,  . Обчислимо
. Обчислимо 
 .
.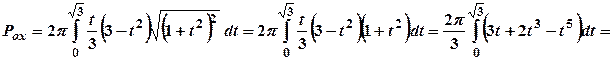
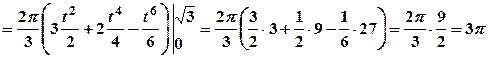 кв. од.
кв. од.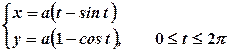 навколо осі
навколо осі  ,
,  .
.
 .
.
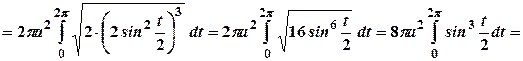


 кв. од.
кв. од. навколо полярної осі.
навколо полярної осі.
 ,
,

 .
.
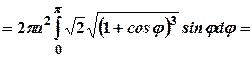


 кв.од.
кв.од. навколо полярної осі.
навколо полярної осі. Обчислимо половину шуканої площі поверхні, а саме:
Обчислимо половину шуканої площі поверхні, а саме: . Знайдемо з рівняння
. Знайдемо з рівняння 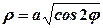 .
.
 .
.
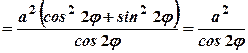 .
.
 .
.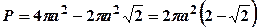 кв. од.
кв. од. ,
,  ,
,  ?
? ,
, 
 ,
,  ,
,  ,
,  ?
? ,
,  ,
, 


