
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Означення визначеного інтеграла як границі інтегральної суми. Умови існування та властивості визначеного інтегралаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нехай функція
Сукупність точок
Означення 1. Якщо існує скінченна границя інтегральної суми
Числа
Означення 2. Функція
Геометричний зміст визначеного інтеграла полягає в тому, що визначений інтеграл від невід’ємної та інтегровної на відрізку
Рис.1.1 Необхідною умовою існування визначеного інтеграла є обмеженість функції Достатньою умовою існування визначеного інтеграла є неперервність функції
Розглянемо деякі властивості визначеного інтеграла: 1) Визначений інтеграл не залежить від позначення змінної інтегрування:
2) Визначений інтеграл з однаковими межами інтегрування дорівнює нулю:
3) Для будь-якого довільного сталого числа
4) При переставленні меж інтегрування визначений інтеграл змінює знак, тобто
5) Якщо функції
6) Якщо функція
7) Якщо функція
Аналогічно маємо, що
8) Якщо функції
9) Якщо функція
10) Якщо функція
11) Якщо функція
Це ствердження має назву теореми про середнє значення визначеного інтеграла. Обчислення визначених інтегралів Формула Ньютона-Лейбніца Для пошуку способу обчислення визначеного інтеграла встановимо зв’язок між невизначеним та визначеним інтегралами. Для цього розглянемо Цей інтеграл називають визначеним інтегралом із змінною верхньою межею. Очевидно, він є функцією від Має місце наступна теорема Барроу: Якщо функція
Тобто для всякої неперервної на Ефективний і простий спосіб обчислення визначеного інтеграла дається формулою Ньютона-Лейбніца:
де
Зразки розв’язування задач Обчислити інтеграли. 1.
Первісною від даної підінтегральної функції є Розв’язування може бути подане у вигляді:
2.
3.
4.
5.
6.
Первісну можна знайти, використавши формулу пониження степеня:
7.
Для знаходження первісної в знаменнику виділимо повний квадрат.
8.
Знайдемо первісну функції. Для цього правильний дріб
Звільнившись від знаменника, маємо:
Отже,
Тоді
Завдання для самостійної роботи Обчислити інтеграли:
1. 2. 3. 4. 5. 6.
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 731; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.197.111 (0.013 с.) |

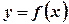 визначена на відрізку
визначена на відрізку  ,
,  <
<  . Розіб’ємо відрізок
. Розіб’ємо відрізок  довільних частин так, щоб
довільних частин так, щоб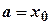 <
<  <
<  …<
…<  <
<  <
<  <…<
<…<  .
.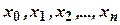 назвемо
назвемо  -розбиттям відрізка
-розбиттям відрізка  та значення функції
та значення функції  у довільній точці
у довільній точці  . Позначимо через
. Позначимо через  - найбільшу довжину серед довжин частинних відрізків, тобто
- найбільшу довжину серед довжин частинних відрізків, тобто 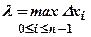 . Утворимо суму
. Утворимо суму  , яка називається інтегральною сумою функції
, яка називається інтегральною сумою функції  на відрізку
на відрізку  .
. при умові, що найбільша із різниць
при умові, що найбільша із різниць  прямує до нуля, яка не залежить ані від способу розбиття відрізка
прямує до нуля, яка не залежить ані від способу розбиття відрізка  у кожному з частинних відрізків, то вона називається визначеним інтегралом функції
у кожному з частинних відрізків, то вона називається визначеним інтегралом функції  . Отже, згідно з означенням,
. Отже, згідно з означенням, .
. - підінтегральним виразом;
- підінтегральним виразом;  - змінною інтегрування, а відрізок
- змінною інтегрування, а відрізок  ,
,  та віссю
та віссю  :
:
 .
. .
. справджується рівність:
справджується рівність: .
. .
. - інтегровні на відрізку
- інтегровні на відрізку  також є інтегровною на цьому відрізку, причому
також є інтегровною на цьому відрізку, причому .
. ,
,  , то вона інтегровна і в двох інших і для будь-якого взаємного розташування точок
, то вона інтегровна і в двох інших і для будь-якого взаємного розташування точок  має місце рівність
має місце рівність
 .
. <
<  і всюди на цьому відрізку
і всюди на цьому відрізку  , то
, то .
. , якщо
, якщо  .
. , то
, то .
. також інтегровна на цьому відрізку, причому
також інтегровна на цьому відрізку, причому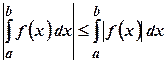 .
. і
і  - відповідно її найменше і найбільше значення на цьому відрізку, то справджуються нерівності
- відповідно її найменше і найбільше значення на цьому відрізку, то справджуються нерівності .
. така, що виконується рівність:
така, що виконується рівність: .
. , де функція
, де функція  та інтегровною на ньому,
та інтегровною на ньому,  .
. для усіх
для усіх  .
. ,
, - яка-небудь її первісна.
- яка-небудь її первісна. .
. . Обчислимо її значення при верхній границі
. Обчислимо її значення при верхній границі  , при нижній границі
, при нижній границі  . За формулою Ньютона-Лейбніца значення інтегралу становить
. За формулою Ньютона-Лейбніца значення інтегралу становить 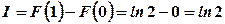 .
. .
.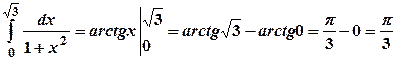 .
.
 .
.
 .
.
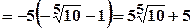 .
. .
. . Отримаємо:
. Отримаємо:
 .
. .
.

 .
. .
. представимо у вигляді суми найпростіших дробів, а саме
представимо у вигляді суми найпростіших дробів, а саме .
. .
.
 .
.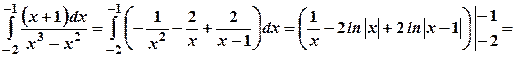

 .
. ;
; ;
; ;
; ;
; ;
; ;
;


