
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальний висновок про квадратні рівнянняСодержание книги
Поиск на нашем сайте Многочленом (поліномом) степеня де Теорема 1 (теорема Безу). При діленні многочлена Д о в е д е н н я. При діленні Ця рівність справедлива при всіх значеннях Якщо Наслідок. Якщо де Якщо рівняння має вигляд Природно виникає питання: чи всяке рівняння має корені? Не всяке рівняння має корені. Але у випадку алгебраїчного рівняння відповідь на це питання позитивна. Теорема 2 (основна теорема алгебри). Всяка ціла раціональна функція Ця теорема доводиться у вищій алгебрі. Нехай многочлен Продовжуючи цей процес виділення лінійних множників, дійдемо до многочлена нульового степеня, тобто деякого фіксованого числа. Це число, очевидно, дорівнює Ніяке значення Звідси випливає таке твердження: многочлен степеня Якщо в розкладі (8.14) деякі лінійні множники виявляться однаковими, то їх можна об’єднати. І тоді розклад многочлена на множники буде мати вигляд: При цьому Звідси можна сформулювати наступну теорему. Теорема 3. Всякий многочлен степеня Приведемо без доведення ще одну важливу теорему. Теорема 4. Якщо многочлен Тоді парі спряжених комплексних чисел буде відповідати квадратний тричлен з дійсними коефіцієнтами Якщо число Таким чином, многочлен з дійсними коефіцієнтами можна розкласти на множники з дійсними коефіцієнтами першого та другого степеня відповідної кратності: Елементи лінійної алгебри.
Визначники вищих порядків. Теорема 1.1 (Лапласа). Визначник дорівнює сумі добутків елементів довільного рядка (стовпця) на їх алгебраїчні доповнення. Наприклад, для визначника третього порядку виконуються такі рівності: Теорема 1.2. Сума добутків елементів довільного рядка (стовпця) на алгебраїчні доповнення іншого рядка (стовпця) дорівнює нулю. Наприклад, для визначника третього порядку виконуються такі рівності:
N.B. Теореми 1.1 і 1.2 мають місце для визначників будь-якого порядку. Розглянемо визначник n-го порядку
За теоремою 1.1 цей визначник дорівнює сумі добутків елементів довільного рядка (стовпця) на їх алгебраїчні доповнення. Наприклад, розклад визначника за елементами першого рядка такий:
Def. Визначником n-го порядку
називають алгебраїчну суму всіх можливих добутків, які містять по одному елементу з кожного рядка і кожного стовпця. Знак кожного доданка дорівнює Усього таких доданків n! Половину з них беруть зі знаком плюс, а іншу половину – зі знаком мінус. N.B. Визначник n-го порядку, у якого під головною діагоналлю всі елементи нульові, дорівнює добутку елементів головної діагоналі, тобто
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 405; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 називається функція
називається функція (8.12)
(8.12) ціле число.
ціле число.  називають ще цілою раціональною функцією від
називають ще цілою раціональною функцією від  Коефіцієнти
Коефіцієнти  дійсні або комплексні числа, незалежна змінна
дійсні або комплексні числа, незалежна змінна  може приймати як дійсні, так і комплексні значення. Коренем многочлена називається таке значення змінної
може приймати як дійсні, так і комплексні значення. Коренем многочлена називається таке значення змінної  залишок дорівнює
залишок дорівнює 
 степеня на одиницю нижчого від
степеня на одиницю нижчого від  а залишком буде постійне число
а залишком буде постійне число  Отже. Ми можемо записати рівність
Отже. Ми можемо записати рівність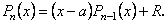 (8.13)
(8.13) що відмінні від
що відмінні від 
 то границя правої частини буде дорівнювати
то границя правої частини буде дорівнювати  а лівої -
а лівої - 
 корінь многочлена, тобто
корінь многочлена, тобто  то
то  а, значить, його можна представити у вигляді добутку
а, значить, його можна представити у вигляді добутку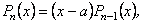
 многочлен.
многочлен. де
де 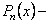 многочлен степеня
многочлен степеня  то таке рівняння називається алгебраїчним рівнянням степеня
то таке рівняння називається алгебраїчним рівнянням степеня  Із визначення випливає, що корені алгебраїчного рівняння
Із визначення випливає, що корені алгебраїчного рівняння  такі ж, як і корені многочлена
такі ж, як і корені многочлена 
 Тоді із наслідка теореми Безу маємо
Тоді із наслідка теореми Безу маємо  Із основної теореми алгебри випливає, що
Із основної теореми алгебри випливає, що  Тоді
Тоді і
і 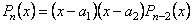 і т.д.
і т.д. так що будемо мати рівність
так що будемо мати рівність (8.14)
(8.14) , що відмінне від
, що відмінне від  , не може бути коренем многочлена
, не може бути коренем многочлена 

 Корінь
Корінь  називається коренем кратності
називається коренем кратності  або
або  коренем кратності
коренем кратності  і т.д.
і т.д. то він має і спряжений корінь
то він має і спряжений корінь 

 є коренем кратності
є коренем кратності  то й число
то й число  буде коренем кратності
буде коренем кратності  і їм буде в розкладі відповідати множник
і їм буде в розкладі відповідати множник 

 (розклад за елементами першого рядка);
(розклад за елементами першого рядка); (розклад за елементами другого стовпця).
(розклад за елементами другого стовпця). ,
,  .
. .
.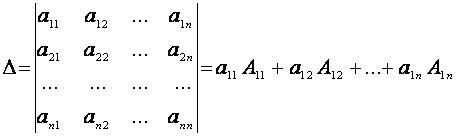 .
. , де
, де  – число інверсій у других індексах за умови, що елементи (множники
– число інверсій у других індексах за умови, що елементи (множники  ) доданка розміщені в порядку зростання перших індексів. Отже,
) доданка розміщені в порядку зростання перших індексів. Отже, .
.



