Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однорідні диференціальні рівняння. Загальні поняття.Содержание книги
Поиск на нашем сайте
Функція Наприклад: Дана функція є однорідною функцією другого виміру, тому що:
Дана функція є однорідною функцією нульового виміру, тому що:
Диференціальне рівняння
Буде однорідним тоді і тільки тоді, коли функції Нехай рівняння має вигляд:
Нехай дані функції
Робимо заміну Тепер підставляємо все це у наше рівняння:
Або це те саме, що
Скоротивши на
Згрупувавши одержане рівняння зі змінними, що розділяються:
Взявши інтеграли та замінивши
Рівняння, що зводяться до однорідних Нехай маємо рівняння виду
Розглянемо два випадки: 1) Тоді система алгебраїчних рівнянь
Має єдиний розв’язок (х0,у0). Проведемо заміну х=х1+х0 у=у1+у0, та отримаємо
Оскільки (х0,у0) є розв’язком системи алгебраїчних рівнянь, то диференціальне рівняння матиме вигляд:
І є однорідним нульового степеня. Отже, робимо заміну у1=ux1 dy1=udx1+x1du Ділимо на dx1
Домножимо на dx1, отримаємо
Об’єднуємо dx з x, du з u, отримаємо
Шукаємо інтеграл
Загальний інтеграл диференціального рівняння матиме вигляд:
2) Робимо заміну dz=a2 dx1+b2dy
Підставимо диференціальне рівняння (1) і одержимо
Звідси,
Загальний інтеграл диференціального рівняння матиме вигляд:
Лінійні диференціальні рівняння першого порядку Рівняння y ’+ p (x)⋅ y = q (x), в якому невідома функція y і її похідна y ′ входять до рівняння у першому степеню і не множаться між собою, p (x) і q (x) – неперервні на деякому проміжку функції, називається лінійним диференціальним рівнянням першого порядку. Розв'язок y (x) цього рівняння шукають у вигляді добутку двох невідомих функцій u (x) і v (x), тобто y = u ⋅ v. Тоді похідна функції приймає вигляд y ′ = u ′ v + v ′ u. Значення y (x) і y ′ підставляють у рівняння y ’+ p (x)⋅ y = q (x) і отримують вираз: u ′ v + uv ′+ p (x) uv = q (x) або u ′ v + u [ v ′+ p (x) v ]= q (x). Функцію v визначають із умови, що вираз в дужках дорівнює нулю, тобто розв'язують рівняння, яке буде завжди з відокремлюваними змінними:
Потім значення v підставляють у рівняння u ′ v = q (x) і з отриманого диференціального рівняння теж з відокремлюваними змінними знаходять загальний розв'язок u = u (x, C). Значення v і u підставляють у рівність y = u ⋅ v і визначають загаль- ний розв'язок лінійного диференціального рівняння.
Рівняння Бернуллі Рівняння виду Розділимо рівняння на уm, то одержимо
Зробимо заміну
Підставимо заміну в рівняння
Рівняння Рікатті Рівняння виду В загальному випадку рівняння Рікатті не інтегрується, відомо лише деякі частинні випадки рівняння рікатті, що інтегруються в квадратурах, розглянемо один із даних випадків. Нехай відомий один частинний розвязок
Розкривши дужки і використовуючи вказану тотожність, одержимо
Перепишемо це рівняння наступним чином:
Отже ми отримали рівняння Бернуллі. Рівняння в повних диференціалах Рівняння виду Розглянемо, яким чином відбудеться інтегрування рівнянь в повних диференціалах, якщо для рівняння (1) виконується умова (2), то неві дома функція U(x,y) задовольняє рішення Інтегруючи рівність (3) по х визначимо функцію U(x,y) з точністю до довільної диф. функція
Інтегруючий множник В деяких випадках рівняння виду
Таким чином замість звичайного диференціального рівняння відносно функції у(х) одержимо диференціальне рівняння в частинних похідних відносно функції В цьому випадку одержимо Проінтегрувавши ліву і праву частину отримаємо
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 457; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 називається однорідною функцією n – го виміру відносно змінних у та х, якщо для довільного числа
називається однорідною функцією n – го виміру відносно змінних у та х, якщо для довільного числа 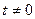 виконується тотожність
виконується тотожність  .
.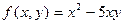
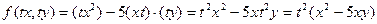


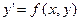 (2) називається однорідним, якщо функція
(2) називається однорідним, якщо функція 
 будуть однорідними функціями одного і того самого виміру.
будуть однорідними функціями одного і того самого виміру.


 тоді
тоді 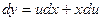 .
.

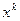 і розкривши дужки, отримаємо
і розкривши дужки, отримаємо


 отримаємо загальний інтеграл:
отримаємо загальний інтеграл: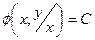

 ,
,  ,
, ,
, .
.




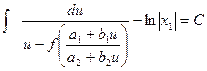

 , тобто коефіцієнти лінійно залежні і
, тобто коефіцієнти лінійно залежні і 

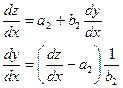
 , а це те саме, що
, а це те саме, що 







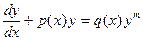 , де
, де 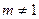 називається рівнянням Бернуллі.
називається рівнянням Бернуллі.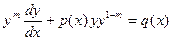



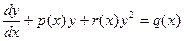 називають рівнянням Рікатті.
називають рівнянням Рікатті. , робимо заміну
, робимо заміну 
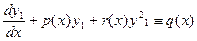


 називається рівнянням в повних диференціалах, якщо його ліва частина є повним диференціалом деякої функції U(x,y), тобто
називається рівнянням в повних диференціалах, якщо його ліва частина є повним диференціалом деякої функції U(x,y), тобто  . В цьому випадку загальний інтеграл рівняння 1 матиме вигляд U(x,y)=С, С – довільна стала. Для того, щоб рівняння 1 було рівнянням в повних диференціалах, необхідно і достатньо щоб
. В цьому випадку загальний інтеграл рівняння 1 матиме вигляд U(x,y)=С, С – довільна стала. Для того, щоб рівняння 1 було рівнянням в повних диференціалах, необхідно і достатньо щоб  .
. .
. , тобто
, тобто  . Диференціюючи рівність (5) по у і враховуючи рівність (4), отримаємо рівняння для знаходження функції
. Диференціюючи рівність (5) по у і враховуючи рівність (4), отримаємо рівняння для знаходження функції  .
. така, що рівняння
така, що рівняння  , то рівняння буде рівнянням в повних диференціалах та достатньо умов цього є рівність; необхідно і достатньо
, то рівняння буде рівнянням в повних диференціалах та достатньо умов цього є рівність; необхідно і достатньо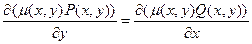
 відома функція.
відома функція.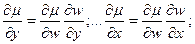 після підстановки в рівняння одержимо
після підстановки в рівняння одержимо