
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Середня гармонійна та методика її обчислення.Содержание книги
Поиск на нашем сайте Середня гармонійна – обернена до середньої арифметичної, обчисленої з обернених значень усередню вальної ознаки. Залежно від характеру наявного матеріалу її застосовують тоді, коли ваги доводиться, множити на обернене їх значення. Таким чином середня гармонійна розраховується, коли відомі дані про обсяг ознаки та індивідуальні значення ознаки (Х) і невідомі ваги (f). Так як обсяги ознак являють собою добуток значень ознаки (Х) на частоту (f), то частоту (f) визначають як f = 1/x. середньою гармонічною простою називають:
Цей розрахунок зроблено за формулою середньої гармонічної зваженої:
де Zj = xj fj — обсяг значень ознаки (у нашому прикладі — вартість). У разі, коли осереднювана ознака є відношенням між логічно пов’язаними величинами (наприклад, відносна величина інтенсивності, структури тощо), постає питання про вибір виду середньої. Основою вибору є логічна формула показника 27 питання. Середня хронологічна,її суть і методика обчислення Середня хронологічна розраховується при аналізі показників, які задані дискретно, тобто у формі величин, що характеризують явище на пені моменти часу, певні дати. Якщо показники характеризують аналізоване явище за період, розбитий на рівні проміжки часу, то середня величина у таких випадках визначається як середня хронологічна
де п – число моментів. Середня хронологічна застосовується переважно в бухгалтерському обліку для визначення середньорічних залишків матеріальних цінностей (за квартал, за рік).
28 питання. Обчислення середніх величин за інтервальним рядом Середня величина в статистиці – це узагальнюючий показник, що характеризує типовий рівень варіюючої ознаки в якісно однорідній сукупності. Середня арифметична застосовується при обчисленні середнього рівня варіюючої ознаки. Середня квадратична застосовується для визначення міри варіації, а середня геометрична – для характеристики середнього темпу росту, тобто в рядах динаміки. При обчисленні середніх величин знаменник кожного з наведених співвідношень виступає як вага і називається частотою (f): 1) середня арифметична. Ця середня величина застосовується у випадках, коли обсяг варіюючої ознаки обчислюється як сума індивідуальних її значень х 1, х 2, х 3, ... хn. Це може бути вік окремих студентів. Середня в цьому разі обчислюється за формулою середньої арифметичної простої, якщо дані не згруповані: Якщо ж окремі варіанти повторюються різне число разів, тобто в наявності ряд розподілу, то для обчислення середнього значення застосовується так звана середня арифметична зважена: Середня арифметична зважена застосовується також при обчисленні середньої з інтервального ряду розподілу та при обчисленні загальної середньої з групових середніх. Результат обчислення середньої з інтервального ряду є дещо наближеним. Як варіанти в цьому випадку використовуються середні значення кожного інтервалу. 2) середня гармонійна є оберненою з так званих обернених значень. Мова йде про те, що середня обчислюється не з варіант x 1, x 2, x 3,..., xn, а з варіант
Широке застосування має середня гармонійна зважена Використовується у випадках, коли відсутні дані про вагу, тобто відсутня f.
29 питання. Характеристика центру розподілу: середня прогресивна,мода,медіана Центром тяжіння будь-якої статистичної сукупності є типовий рівень ознаки, узагальнююча характеристика всього розмаїття її індивідуальних значень. Такою характеристикою є середня величина
В інтервальних рядах, припускаючи рівномірний розподіл елементів сукупності в межах j -го інтервалу, як варіанту Окрім типового рівня важливе значення має домінанта, тобто найбільш поширене значення ознаки. Таке значення називають модою (Мо). У дискретному ряду моду визначають безпосередньо за найбільшою частотою (часткою). В інтервальному ряду за тим самим принципом визначається модальний інтервал, а в разі потреби конкретне модальне значення в середині інтервалу обчислюється за інтерполяційною формулою
Для моди як домінанти число відхилень (х – Мо) мінімальне. Оскільки мода не залежить від крайніх значень ознаки, то її доцільно використовувати тоді, коли ряд розподілу має невизначені межі. Характеристикою центра розподілу вважається також медіана (Ме) — значення ознаки, яке припадає на середину впорядкованого ряду, поділяє його навпіл — на дві рівні за обсягом частини. Визначаючи медіану, використовують кумулятивні частоти В інтервальному ряду за цим принципом визначають медіанний інтервал, а значення медіани в середині інтервалу, як і значення моди, обчислюють за інтерполяційною формулою:
30 питання. Суть варіації масових явищ. Статистичні характеристики варіації На основі характеристик варіації оцінюється інтенсивність структурних зрушень, щільність взаємозв’язків соціально-економічних явищ, точність результатів вибіркового обстеження. Для вимірювання та оцінювання варіації використовуються абсолютні та відносні характеристики. До абсолютних належать: варіаційний розмах, середнє лінійне та середнє квадратичне відхилення, дисперсії; відносні характеристики подаються низкою коефіцієнтів варіації, локалізації, концентрації. Варіаційний розмах R — це різниця між максимальним і мінімальним значеннями ознаки: R = x max – x min. Він характеризує діапазон варіації, наприклад родючості ґрунтів у регіоні, продуктивності праці в галузях промисловості тощо. Узагальнюючою характеристикою варіації є середнє відхилення: а) лінійне
б) квадратичне, або стандартне
в) дисперсія (середній квадрат відхилень)
На підставі первинних, незгрупованих даних наведені характеристики обчислюють за принципом незваженої середньої:
Середнє лінійне Коефіцієнти варіації: лінійний квадратичний осциляції Якщо центр розподілу поданий медіаною, то за відносну міру варіації беруть квартильний коефіцієнт варіації
Для оцінювання ступеня варіації застосовують також співвідношення децилів. Так, коефіцієнт децильної диференціації показує кратність співвідношення дев’ятого та першого децилів:
31 питання. Дисперсія,методика обчислення і властивості дисперсій Дисперсія — це середній квадрат відхилень індивідуальних значень ознаки від середньої:
Як і будь-яка середня, дисперсія має певні математичні властивості. Сформулюємо найважливіші з них. 1. Якщо всі значення варіант xj зменшити на сталу величину А, то дисперсія не зміниться:
2. Якщо всі значення варіант xj змінити в А раз, то дисперсія зміниться в A 2 раз:
3. Якщо частоти замінити частками, дисперсія не зміниться. Загальна дисперсія характеризує варіацію ознаки у навколо загальної середньої:
Групова дисперсія характеризує варіацію відносно групової середньої:
Оскільки в групи об’єднуються певною мірою схожі елементи сукупності, то варіація в групах, як правило, менша, ніж у цілому по сукупності. Якщо причинні комплекси, що формують варіацію в різних групах, неоднакові, то й групові дисперсії різняться між собою. Узагальнюючою мірою внутрішньогрупової варіації є середня з групових дисперсій:
Різними є й групові середні
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 842; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

 =
= 
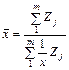 ,
, за формулою:
за формулою: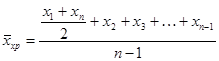 ,
, .
. .
.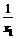 ,
,  ,
,  ,...,
,...,  :
: – середня гармонійна проста. Застосовується на практиці дуже рідко.
– середня гармонійна проста. Застосовується на практиці дуже рідко.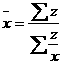
 , де z = xf.
, де z = xf. . За даними ряду розподілу середня обчислюється як арифметична зважена; вагами є частоти fj або частки dj:
. За даними ряду розподілу середня обчислюється як арифметична зважена; вагами є частоти fj або частки dj: ,
, 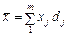 , де j — номер групи; m — число груп.
, де j — номер групи; m — число груп. використовують середину інтервалу. При цьому ширину відкритого інтервалу умовно вважають такою самою, як сусіднього закритого інтервалу.
використовують середину інтервалу. При цьому ширину відкритого інтервалу умовно вважають такою самою, як сусіднього закритого інтервалу. , де
, де  та h — відповідно нижня межа та ширина модального інтервалу,
та h — відповідно нижня межа та ширина модального інтервалу,  ,
,  ,
, 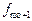 — частоти (частки) відповідно модального, передмодального та післямодального інтервалів.
— частоти (частки) відповідно модального, передмодального та післямодального інтервалів.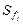 або частки
або частки  . У дискретному ряду медіаною буде значення ознаки, кумулятивна частота якого перевищує половину обсягу сукупності, тобто
. У дискретному ряду медіаною буде значення ознаки, кумулятивна частота якого перевищує половину обсягу сукупності, тобто 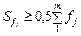 (для кумулятивної частки
(для кумулятивної частки 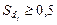 ).
). , де x 0 та h — відповідно нижня межа та ширина медіанного інтервалу; f me — частота медіанного інтервалу;
, де x 0 та h — відповідно нижня межа та ширина медіанного інтервалу; f me — частота медіанного інтервалу;  — кумулятивна частота передмедіанного інтервалу.
— кумулятивна частота передмедіанного інтервалу. ;
; ;
; .
. або
або  .
. та середнє квадратичне
та середнє квадратичне 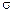 відхилення є безпосередніми мірами варіації.
відхилення є безпосередніми мірами варіації. ;
; ;
;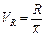 .
. .
.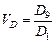 .
.
 .
. .
. .
. .
. .
. .
. . Мірою варіації їх навколо загальної середньої є міжгрупова дисперсія
. Мірою варіації їх навколо загальної середньої є міжгрупова дисперсія .
.


