
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття про середні величини їх значення та види.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Середня величина є узагальнюючою мірою ознаки, що варіює, у статистичній сукупності. Показник у формі середньої характеризує рівень ознаки в розрахунку на одиницю сукупності. Як уже зазначалося, значення ознаки j -го елемента поєднує в собі як спільні для всієї сукупності типові риси, так і притаманні лише цьому елементу індивідуальні особливості. Абстрагуючись від індивідуальних особливостей окремих елементів, можна виявити те загальне, типове, що властиве всій сукупності. Взаємозв’язок індивідуальних значень ознаки та середньої — це діалектична єдність загального і окремого. Замінюючи множину індивідуальних значень, середня не змінює визначальної властивості сукупності — загального обсягу явища. Зв’язок визначальної властивості з елементами сукупності описується функцією f (x 1, x 2,... xn), яка виражає певну математичну дію над емпіричними значеннями ознаки (підсумовування, множення, степенювання, коренювання) і визначає вид середньої. Так, у разі підсумовування значень ознаки визначальну властивість забезпечує середня арифметична, при множенні — середня геометрична і т. д. Отже, при обчисленні середніх у соціально-економічних дослідженнях необхідно чітко усвідомити визначальну властивість сукупності та логіко-математичну суть — логічну формулу — показника. Наприклад, логічна формула середнього вкладу в банк:
Чисельник логічної формули середньої являє собою обсяг значень (визначальну властивість) ознаки, що варіює, а знаменник — обсяг сукупності. Як правило, визначальна властивість — це реальна абсолютна чи відносна величина, яка має самостійне значення в аналізі. У кожному конкретному випадку для реалізації логічної формули використовується певний вид середньої, зокрема: а) середня арифметична (проста, зважена); б) середня гармонічна (проста, зважена); в) середня геометрична; г) середня квадратична; д) середня хронологічна; е) середня прогресивна. Залежно від характеру первинної інформації середня будь-якого виду може бути простою чи зваженою. Позначається середня символом Середня арифметична методика її обчислення та математичні властивості. Середня арифметична Оскільки для більшості соціально-економічних явищ характерна адитивність обсягів (виробництво цукру, витрати палива тощо), то найпоширенішою є арифметична середня, яка обчислюється діленням загального обсягу значень ознаки на обсяг сукупності. За первинними, незгрупованими даними обчислюється середня арифметична проста:
У великих за обсягом сукупностях окремі значення ознаки (варіанти) можуть повторюватись. У такому разі їх можна об’єднати в групи (j = 1, 2,..., m), а обсяг значень ознаки визначити як суму добутків варіант хj на відповідні їм частоти fj, тобто як
Вагами можуть бути частоти або частки (відносні величини структури), іноді інші величини (абсолютні показники). Середня не збігається з жодним значенням ознаки, але це типовий рівень кваліфікації налагоджувачів фірми. Формально між середньою арифметичною простою і середньою арифметичною зваженою немає принципових відмінностей. Адже багаторазове (f раз) підсумовування значень однієї варіанти замінюється множенням варіант х на вагу f. Проте функціонально середня зважена більш навантажена, оскільки враховує поширеність, повторюваність кожної варіанти і певною мірою відображує склад сукупності. Значення середньої зваженої залежить не лише від значень варіант, а й від структури сукупності. Чим більшу вагу мають малі значення ознаки, тим менша середня, і навпаки. Наприклад, незважаючи на той факт, що в двох регіонах мешкають люди різного віку, у тому регіоні, де більше дітей, середній вік населення буде менший. На цю властивість середніх слід зважати при використанні їх у порівняльному аналізі сукупностей, склад яких істотно різний. У таких випадках, аби елімінувати (усунути) вплив структури сукупності на середню, вдаються до пошуку стандартизованих ваг. У структурованій сукупності при розрахунку середньої зваженої варіантами можуть бути як окремі значення ознаки, так і групові середні
Обчислену так середню на відміну від групових називають загальною. Середня арифметична має певні властивості, які розкривають її суть. 1. Алгебраїчна сума відхилень окремих варіант ознаки від середньої дорівнює нулю:
тобто в середній взаємно компенсуються додатні та від’ємні відхилення окремих варіант. 2. Сума квадратів відхилень окремих варіант ознаки від середньої менша, ніж від будь-якої іншої величини:
3. Якщо всі варіанти збільшити (зменшити) на одну й ту саму величину А або в А раз, то й середня зміниться аналогічно. Аналітичні можливості центрованого середнього балу ширші, ніж середньозваженого. Центрований бал може бути додатною чи від’ємною величиною. Знак свідчить про позитивну чи негативну оцінку явища. За допомогою центрованого балу можна порівняти оцінки різних явищ незалежно від розмірності шкали. Для такого порівняння можна скористатися формулою переходу від середньозваженого до центрованого балу:
4. Значення середньої залежить не від абсолютних значень ваг, а від пропорцій між ними. При пропорційній зміні всіх ваг середня не зміниться. Згідно з цією властивістю замість абсолютних ваг — частот fj — можна використати відносні ваги у вигляді часток
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 547; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.59.124 (0.01 с.) |

 .
. (риска над символом означає осереднення індивідуальних значень) і вимірюється в тих самих одиницях, що й ознака.
(риска над символом означає осереднення індивідуальних значень) і вимірюється в тих самих одиницях, що й ознака.
 . Такий процес множення у статистиці називають зважуванням, а число елементів сукупності з однаковими варіантами — вагами. Сама назва «ваги» відбиває факт різновагомості окремих варіант. Значення ознаки осереднюються за формулою середньої арифметичної зваженої:
. Такий процес множення у статистиці називають зважуванням, а число елементів сукупності з однаковими варіантами — вагами. Сама назва «ваги» відбиває факт різновагомості окремих варіант. Значення ознаки осереднюються за формулою середньої арифметичної зваженої:
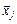 , кожна з яких має відповідну вагу у вигляді групових частот fj:
, кожна з яких має відповідну вагу у вигляді групових частот fj:
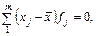


 або процентів 100 dj:
або процентів 100 dj: .
.


