
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Середні величини та показники варіації. Структурні середні величини.Содержание книги
Поиск на нашем сайте
При вивчені масових явищ одна з основних задач статистики є вивчення окремих властивостей кожної сукупності явища. Для того щоб виявити характерні особливості сукупності, використовують середні величини. Середня величина характеризує всю вагу одиниць сукупності. В статистиці використовують декілька видів середніх величин. Основними серед них є: середня арифметична, середня гармонічна, середня квадратична і середня геометрична Середня арифметична – основний вид середніх величин. Буває проста і зважена. Проста – це сума індивідуальних значень варіїруючої ознак, що поділена на кількість одиниць сукупності. Зважена – середня із варіантів, що повторюється не однакову кількість раз чи має різну статистичну вагу. Середня квадратична використовується для оцінки варіації, тобто коли треба оцінити середню варіацію ознаки. Середнє гармонійне і середнє геометричне в даному випадку не знаходимо. Середня арифметична проста:
де Хі – індивідуальні значення ознаки; n – кількість одиниць сукупності.
Середня арифметична зважена. Оскільки сукупність згрупована, а частоти варіантів задані явно, то визначаємо середню арифметичну зважену величину:
де Хі – індивідуальні значення ознаки; mі – кількість однакових варіант. Структурні середні характеризують структуру аріаційних рядів. До них відносяться мода і медіана. Вони виражають визначене значення ознаки у ряду розподілу. Мода – значення ознаки, що найбільш часто повторюється. Медіаною називається значення ознаки, що знаходиться в середині ранжируємого ряду і поділяє цей ряд на дві рівні частини Структурні середні а) визначення моди:
де Х0– нижня границя модального інтервалу; і – величина інтервалу; mMo ‑ відносна частота модального інтервалу; mMo-1 ‑ відносна частота, передуючого модальному, інтервалу; mMo+1 – відносна частота, наступного після модального, інтервалу.
б) визначення медіани:
де Х0 – нижня границя медіанного інтервалу; і – величина інтервалу; mі – загальна сума частот усіх інтервалів; mе – частота медіанного інтервалу; Sme - 1 – сума частот до медіанного інтервалу. Крім визначення середніх величин в цьому пункті курсової роботи знаходимо показники варіації. Вони показують коливність ознаки у сукупності. До них відносяться: розмах варіації, середньо лінійні відхилення, середньоквадратичні відхилення і дисперсія Показники варіації: а) середньоквадратичне відхилення - показує наскільки в середньому індивідуальне значення відхиляється від середнього, але з врахуванням знаку.
б) дисперсія
Відносні показники варіації (коефіцієнти варіації) – необхідні для того, щоб порівняти варіацію різних ознак в різних сукупностях. Застосовується для оцінки однорідності сукупності. Якщо коефіцієнт варіації більше 30%, то вважають що сукупність неоднорідна. а) лінійний
б) квадратичний
1) Проведемо розрахунок середніх показників та показників варіації за кількісною ознакою – стаж роботи (роки). Для цього, використовуємо структурне групування таблиця №8:
Середні показники: 1)Середнє арифметичне:
2) Мо = 1+3 3)Ме = 4+3 4) Розмах варіації: R =19-1=18 (роки) – показує, що варіруюча ознака змінюється у межах 18 років. 5) Середньо-лінійне відхилення: Л = = 6)Середньоквадратичне відхилення: 7) Дисперсія:
відхилення індивідуальних значень кількісної ознаки від середнього значення становить 13,53 років. 8) Коефіцієнти варіації:
1) Проведемо ще один розрахунок середніх показників та показників варіації за кількісною ознакою – продуктивність праці (т/год). Дані беремо з таблиці структурного групування (таблиця №9):
1)Середнє арифметичне:
2) Мо =121+15,3* 3) Ме =131,6+5,3* 4) Розмах варіації: R =153 – 121 = 32 (т/год) – показує, що варіруюча ознака змінюється у межах 32 (т/год). 5) Середньо-лінійне відхилення: Л =( + 6) Середньоквадратичне відхилення:
7)Дисперсія:
8)Коефіцієнти варіації:
3) Проведемо розрахунок середніх показників та показників варіації за кількісною ознакою – час у русі (год) використовуючи структ. груп.(таб №10):
1) Середнє арифметичне:
2) Мо =32+3,2 3) Ме =4,1+3,2 4) Розмах варіації: R =51-32=19 (год) – показує, що ознака змінюється у межах 19 (год). 5) Середньо лінійне відхилення: Л =(
6) Середньоквадратичне відхилення:
7) Дисперсія:
8) Коефіцієнти варіації:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 370; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.102.163 (0.008 с.) |

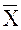 = SХі / n (3.4)
= SХі / n (3.4) ; (3.5)
; (3.5) ; (3.6)
; (3.6) (3.7)
(3.7) (3.8)
(3.8) (3.9)
(3.9) (3.10)
(3.10) (3.11)
(3.11) =(2,5*9)+(5,5*7)+(8,5*8)+(11,5*3)+(14,5*0)+(17,5*1)=181/28≈6,5
=(2,5*9)+(5,5*7)+(8,5*8)+(11,5*3)+(14,5*0)+(17,5*1)=181/28≈6,5 =1+3*1,3 ≈ 4,9 (роки) – на АТП найчастіше зустрічаються водії зі стажем ≈ 4,9 років.
=1+3*1,3 ≈ 4,9 (роки) – на АТП найчастіше зустрічаються водії зі стажем ≈ 4,9 років.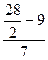 =6,1(роки) – на АТП половина водіїв зі стажем менше 6,1 років, і половина більше.
=6,1(роки) – на АТП половина водіїв зі стажем менше 6,1 років, і половина більше. =
= ≈3,03 (років) – показує, що індивідуальні значення відрізняються від середнього на 3,03 роки (без урахування знаку відхилення).
≈3,03 (років) – показує, що індивідуальні значення відрізняються від середнього на 3,03 роки (без урахування знаку відхилення). =3,68 (роки) відхилення індивідуальних значень кількісної ознаки від середнього значення становить 3,68 років (відхилення відбувається як в одну, так і в іншу сторону)
=3,68 (роки) відхилення індивідуальних значень кількісної ознаки від середнього значення становить 3,68 років (відхилення відбувається як в одну, так і в іншу сторону)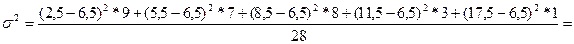 13,53
13,53 46,6% - коефіцієнт більше 30%, отже сукупність не однорідна.
46,6% - коефіцієнт більше 30%, отже сукупність не однорідна. 56,6% - коефіцієнт більше 30%, отже сукупність не однорідна.
56,6% - коефіцієнт більше 30%, отже сукупність не однорідна. ≈ 134,4 т/год
≈ 134,4 т/год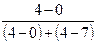 =142,2 (т/год) - на АТП найчастіше зустрічається продуктивність праці 142,2 (т/год).
=142,2 (т/год) - на АТП найчастіше зустрічається продуктивність праці 142,2 (т/год). =133,72 (т/год) – на АТП половина продуктивності праці менше 133,72 т/год, і половина більше.
=133,72 (т/год) – на АТП половина продуктивності праці менше 133,72 т/год, і половина більше.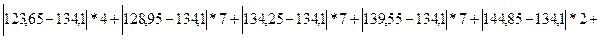
 )/28 ≈ 5,5 (т/год) - показує, що індивідуальні значення відрізняються від середнього на 5,5 т/год (без урахування знаку відхилення).
)/28 ≈ 5,5 (т/год) - показує, що індивідуальні значення відрізняються від середнього на 5,5 т/год (без урахування знаку відхилення).
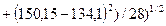 = 6,9 (т/год) - відхилення індивідуальних значень кількісної ознаки від середнього значення становить 6,9 т/год, як в одну, так і в іншу сторону.
= 6,9 (т/год) - відхилення індивідуальних значень кількісної ознаки від середнього значення становить 6,9 т/год, як в одну, так і в іншу сторону.
 = 47 (т/год)- відхилення індивідуальних значень кількісної ознаки від середнього значення становить 47 т/год.
= 47 (т/год)- відхилення індивідуальних значень кількісної ознаки від середнього значення становить 47 т/год.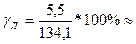 4,1% - коефіцієнт менший 30%, отже сукупність буде однорідна.
4,1% - коефіцієнт менший 30%, отже сукупність буде однорідна. 5,1%- коефіцієнт менший 30%, отже сукупність буде однорідна.
5,1%- коефіцієнт менший 30%, отже сукупність буде однорідна.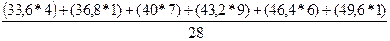 ≈41,7 (год)
≈41,7 (год) 33,8 (год) – на АТП найчастіше зустрічається час у русі 33,8 (год)
33,8 (год) – на АТП найчастіше зустрічається час у русі 33,8 (год) 42,24 (год) – на АТП половина часу у русі автомобіля менше 42,24 год, і половина більше.
42,24 (год) – на АТП половина часу у русі автомобіля менше 42,24 год, і половина більше.
 )/28=3,5 (год)- показує, що індивідуальні значення відрізняються від середнього на 3,5 год (без урахування знаку відхилення).
)/28=3,5 (год)- показує, що індивідуальні значення відрізняються від середнього на 3,5 год (без урахування знаку відхилення).
 = 5,1 (год)- відхилення індивідуальних значень кількісної ознаки від середнього значення становить 5,1 год, як в одну, так і в іншу сторону.
= 5,1 (год)- відхилення індивідуальних значень кількісної ознаки від середнього значення становить 5,1 год, як в одну, так і в іншу сторону.
 = 26,4 (год)- відхилення індивідуальних значень кількісної ознаки від середнього значення становить 26,4 год.
= 26,4 (год)- відхилення індивідуальних значень кількісної ознаки від середнього значення становить 26,4 год. - коефіцієнт менший 30%, отже сукупність буде однорідна.
- коефіцієнт менший 30%, отже сукупність буде однорідна.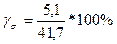 =12,2%- коефіцієнт менший 30%, отже сукупність буде однорідна.
=12,2%- коефіцієнт менший 30%, отже сукупність буде однорідна.


