
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет космічної геодезії і значення її.Содержание книги
Поиск на нашем сайте
Предмет космічної геодезії і значення її. Космічною геодезією називають розділ геодезичної науки, в якому рішення наукових і практичних задач геодезії здійснюються шляхом спостережень штучних супутників Землі. Таким чином в космічній геодезії розв’язують питання пов’язані з визначенням координат супутника і його орбіти, розробляють методи і прилади для спостережень супутників, розробляються методи обчислень необхідних результатів спостережень для визначення тих чи інших елементів задач, що розв’язуються за допомогою супутників. Спостереження супутників дозволяють розв’язувати такі головні задачі: 1. Досліджувати фігуру і гравітаційне поле Землі і визначати зміни цих величин з часом. 2. Визначають координати супутника на орбіті і саму орбіту супутника, що дозволяє по зміні цих величин досліджувати земну поверхню, в тому числі і корисні копалини. 3. Використовувати спостереження супутників для визначення точок земної поверхні і створювати таким чином геодезичні мережі з відповідними координатами їх пунктів. Теоретичними засадами методів космічної геодезії є практичний розв’язок основного рівняння космічної геодезії, записаного в такому вигляді. Нехай точка на земній поверхні Q і супутник в точці С, який знаходиться на орбіті, визначається в геоцентричній системі координат векторами:
З аналізу цього рівняння (1.1) бачимо що воно дає можливість визначити як координати точки земної поверхні Космічна геодезія є важливою частиною геодезичної науки оскільки дозволяє вирішувати не тільки перераховані задачі, а й виконувати зйомку земної поверхні з супутників і використовувати ці знімки для картографування. Системи координат В цій с-мі площину земного екватора приймають за координатну площину. Положення довільної точки М визначається двома координатами: географ. широта і географ. довгота. Широтою називається гострий кут утворений прямовисною лінією в точці спостер. М і площиною екватора. Довготою є двогранний кут при полюсі утворений площинами початкового меридіана і меридіана точки спостереження. Системи виміру часу.
Для фіксації одиниць часу встановлюють точки чи лінії за допомогою яких і фіксують ці одиниці, тому в залежності від вибору точок розрізняють різні системи часу. Відомо, що при фіксації зоряної доби як одиниці зоряного. часу використовують точку весняного рівнодення і меридіан точки спостереження. За добу точка весняного рівнодення буде два рази перетинати меридіан точки спостереження: у точках верхньої кульмінації і нижньої. Зоряною добою є проміжок часу між двома однойменними послідовними кульмінаціями точки весняного рівнодення на меридіані т. спостереження. За початок зоряної доби приймають момент нижньої кульмінації. Мірою зор. часу є годинний кут точки весняного рівнодення. Істинний час. Ця система виміру часу для фіксації одиниці часу використовують центр істинного сонця і меридіан точки спостереження. У своєму видимому русі сонце буде перетинати площину меридіана у двох точках(в. і н. кульмінації). Істинною добою називають проміжок часу між двома послідовними однойменними кульмінаціями центра істинного сонця на меридіані точки спостереження. За початок доби приймають точку нижньої кульмінації. Мірою істинного часу є величина годинного кута. Час, який фіксується за допомогою середнього екваторіального Сонця назив. середнім часом. Середньою добою є проміжок часу між двома послідовними та однойменними кульмінаціями сер. екватор. сонця на меридіані точки спостережень. Середнім екліптичним сонцем назив. фіктивну точку що рухається по екліптиці з рівномірною швидкістю, що = сер. швидк. руху реального сонця за рік. Сер. екваторіальним сонцем є фіктивна точка що рухається по екватору рівномірно зі швидкістю сер. екліпт. сонця. Періодичні зміни в періоді обертання пов’язані з сезонною циркуляцією мас атмосфери. В зимовий період атмосферні маси рухаються в напрямку протилежному до напрямку обертання Землі –гальмівний ефект; а у літній час - співпадає, тобто швид. обертання прискорюється. Ці фактори можуть змінювати період обертання, тому була введена система земного динамічного часу. Одиницею часу є одна ефемеридна секунда 1 сек=1 / 31556925 частина тропічного року. Тривалість тропічного року 365,2422 сер. діб.
Закони руху ШСЗ. Рух супутників по орбіті навколо Землі описується законами Кеплера, які для випадку дослідження руху супутників формулюються так. 1-й закон: орбітою супутника може бути плоска крива другого порядку (коло, еліпс, парабола, гіпербола) в одному із фокусів якої знаходиться Земля. Розглянемо коли орбітою є еліпс. Найближчою точкою орбіти супутника до Землі є точка Перігей, а найбільш віддалена Апогей. Всяка орбіта характеризується двома параметрами: а – велика піввісь, е – ексцентриситети.
Положення супутника на орбіті визначають двома параметрами: r відстань або радіус-вектор супутника і Істина аномалія – кут утворений радіус-вектором супутника і напрямком на Перигей. Цей кут завжди відраховується від напрямку на перігей проти ходу годинникової стрілки і може приймати значення від 0 до 360. 2-й закон: радіус-вектор супутника в рівні проміжки часу описує рівновеликі площі секторів. Нехай супутник один раз находиться в точці С1, а другий в точці С2. Відомо:
У відповідності до другого закону
З аналізу (1.10) встановлюємо, що супутник по орбіті рухається нерівномірно, в районі Перигею ця швидкість досягає максимального значення, а в районі Апогею швидкість руху супутника мінімальна. 3-й закон: відношення квадратів періодів обертання двох супутників по орбітах є величиною постійною і дорівнює відношенню кубів великих півосей їх орбіт.
Якщо супутники, що рухаються мають різну масу то
З-й закон Кеплера дозволяє по відомих періодах обертань супутників визначити параметри орбіти і навпаки. Рух супутників по орбіті, який проходив би у відповідності до законів Кеплера називається незбуреним рухом. Рух супутників в реальному гравітаційному полі Землі завжди пов’язаний із збуренням тих чи інших параметрів руху цим гравітаційним полем і тому називається збуреним рухом. Елементи орбіт ШСЗ. Елементами орбіт називають величини, які характеризують як саму орбіту так і її розміщення в просторі, а також положення супутника на орбіті. Відомо, що орбітою супутника може бути плоска крива коло, еліпс, парабола, гіпербола. Для характеристики орбіти як геометричної фігури достатньо знати: а – велика піввісь, е – ексцентриситети.
Для характеристики орбіти супутника в просторі використовують два параметри: довгота висхідного вузла орбіти, нахил орбіти до екватора. Орбіта всякого супутника буде перетинати площину небесного екватора в двох точках, які називають висхідною точною орбіти і низхідною точкою орбіти. Назви пов’язані із рухом супутника довкруги Землі. Нехай тачка Кутом нахилу орбіти називають кут утворений площиною орбіти з площиною небесного екватора, цей кут від 0 до 90. Наступні дві координати визначають положення супутника на орбіті. Цими координатами є висота Перігею і істина аномалія. Висотою перігея
Положення супутника розглядається кутом істинної аномалії
Наступні елементи орбіти: середній рух супутника середня аномалія ексцентрична аномалія Нехай ми маємо орбіту супутника у вигляді еліпса. Відомо на основі ll закону Кєплера, що рух супутника по орбіті відбувається з різною швидкістю в районі перигея- максимальна, апогея – мінімальна. Для характеристики руху супутника по орбіті часто використовують так званий середній рух який дорівнює середньому значенню швидкості руху супутника по орбіті. Опишемо коло радіуса а і спроектуємо на це коло супутник, кут утворений напрямком на точку перигея орбіти і на точку C`, яка є проекцією супутника на орбіту в виді кола радіуса а, називається ексцентричною аномалією супутника (Е). Нехай супутник сферичну відстань Інтеграл площ. Рівняння (1.14) незбуреного руху помножимо векторно на вектор
Інтегруючи цей вираз отримаємо:
(1.16) є рівнянням, яке називають інтегралом площ. Розпишемо його в координатній формі:
Знайдемо координатні рівняння, що характеризують інтеграл площі:
(1.17) називаються інтегралом площ в координатній формі. Отримаймо рівняння, що характеризує в координатній формі площину орбіти супутника. Нехай координати супутника x, y, z, помножимо на рівняння (1.17) і просумуємо.
Рівняння (1.18) називають рівнянням площини орбіти супутника в координатній формі. Інтеграл енергії Помножимо рівняння (1.14) скалярно на величину
Оскільки
Підставимо (1.20) і (1.19) в вихідне рівняння:
Інтегруємо отриманий вираз:
Рівняння (1.21) називають інтегралом енергії. Воно характеризує ту енергію, яку має супутник рухаючись по орбіті. При чому в (1.21) V характеризує кінетичну енергію супутника, а
Перетворимо праву частину в (1.22) виходячи з того, що для характеристики положення супутника на орбіті можна використовувати фокальний параметр
Підставляючи замість
Інтеграли Лапласа Запишемо диференційне рівняння незбуреного руху:
Помножимо векторно на інтеграл площ
Відомо, що
Зробимо відповідні заміни
Замінимо отриманим виразом праву частину (1.31)
Інтегруємо:
(1.32) – інтеграл Лапласа в векторній формі. Представимо (1.32) в координатній формі:
(1.33) є записом рівняння Лапласа в координатній формі. Розпишемо його по окремих координатах:
Рівняння Лапласа дозволяє отримати формулу інтеграла енергії. Для цього скакярно помножимо (1.32) на вектор f. В результаті перетворень:
Збурений рух ШСЗ Рух супутника за законами Кеплера передбачає ідеальний випадок руху, при якому на супутник впливала би тільки сила тяжіння утворена Землею, як тілом правильної геометричної форми, або абсолютно твердим, або з правильним і незмінним розподілом мас. Для реальної Землі всі ці умови не виконуються, оскільки вона не має правильної геометричної форми, не має правильного розподілу мас, і крім того на супутник будуть діяти сили тяжіння, що утворюють інші небесні тіла, тому реальний рух супутника відбувається по реальних орбітах і такий рух називається збуреним, а орбіта-збуреною. Очевидно, що елементи орбіти супутника(реальної) і елементи, які характеризують положення супутника на реальній орбіті будуть відрізнятися від відповідних елементів незбуреної орбіти. Ці різниці називаються збуреннями відповідних елементів. Очевидну величину збурень можна визначити
В рівнянні (1.54) в правій частині диф. р-ня знаходиться прискорення ω по осях координат X,Y,Z. Ці прискорення і характеризують вплив різноманітних факторів на рух супутника. Безпосереднє інтегрування р-ня (1.54) неможливе, оскільки дуже багато різноманітних факторів впливає на збурення, тому розв’язок цих диф. рівнянь проводять приблизними методами, що дозволяють визначати швидкості
(1.55) і (1.56) дозволяють обчислювати відповідні збурення і через них визначити збурення відповідних елементів орбіти. Вплив мас Сонця і Місяця Дослідженнями встановлено, що на параметри гравітаційного поля Землі впливають не тільки сила тяжіння самої Землі, але й сила тяжіння, що створюється між ситником і іншими тілами сонячної системи. На супутника найбільший вплив мають маси місяця і сонця. Взаємодіючи із супутниками ці маси будуть створювати додаткові сили тяжіння напрямлені по дії лінії, що з’єднує супутник з відповідними небесними тілами. Ці додаткові сили тяжіння будуть старатися змістити супутник з відповідної орбіти по напрямку дії цих сил, що приведе до додаткових збурень у відповідних елементах орбіти. Якщо R=2000, то вплив маси Землі на супутник буде в 140 раз більший за вплив маси Місяця. Якщо R=200 тис., то вплив маси Землі на супутник буде в 2 раз більший за вплив маси Місяця. Вплив сонячного тиску. Дослідженнями встановлено, що сонячні промені попадаючи на ту чи іншу поверхню здійснюють тиск на цю поверхню.
P – площа поперечного перерізу супутника S – потужність сонячної радіації на одиницю площі K – коефіцієнт відбивання C – швидкість розповсюдження світла R – відстань від землі до сенця Δ – відстань від супутника до сонця α – кут падіння сонячних променів на поверхню Сила F здійснює тиск на поверхню супутника і старається змістити його з своєї орбіти. Супутники системи GPS Система супутників NAUSTAR має 24 робочих супутника, з орбітальним періодом 12 годин на висоті 20200 км від поверхні землі в 6 різних площинах, що мають нахил до екватора 55 градусів, розташовану по 4 супутника.3 з цих супутника є резервними і готові підключитися до системи в будь-який момент часу при виході з ладу якогось із супутників. Вказана висота необхідна для забезпечення стабільності орбітального руху і зменшення фактору впливу опору атмосфери. На кожному із супутників розташовані атомні годинники, які вимірюють час з точністю 1 нс. В GPS вимірювання є трьохмірними, і їх не можна розділити на планові і висотні. Швидкість GPS сигналу близька до швидкості світла, знаючи час необхідний сигналу, для того щоб досягнути приймача, можна розрахувати віддаль. Точність навігаційних вимірювань досягається використанням двох видів GPS-сигналів, що передаються із супутників: 1)навігаційне повідомлення, що містить тижневий альманах положення супутників на небесній сфері. 2)код вільного доступу с/а, який використовується для розрахунку віддалей між антеною приймача і супутником. Вимірювання проводимо в тому випадку, коли наш приймач отримає сигнали одночасно від не менше як 4-х супутників
Предмет космічної геодезії і значення її. Космічною геодезією називають розділ геодезичної науки, в якому рішення наукових і практичних задач геодезії здійснюються шляхом спостережень штучних супутників Землі. Таким чином в космічній геодезії розв’язують питання пов’язані з визначенням координат супутника і його орбіти, розробляють методи і прилади для спостережень супутників, розробляються методи обчислень необхідних результатів спостережень для визначення тих чи інших елементів задач, що розв’язуються за допомогою супутників. Спостереження супутників дозволяють розв’язувати такі головні задачі: 1. Досліджувати фігуру і гравітаційне поле Землі і визначати зміни цих величин з часом. 2. Визначають координати супутника на орбіті і саму орбіту супутника, що дозволяє по зміні цих величин досліджувати земну поверхню, в тому числі і корисні копалини. 3. Використовувати спостереження супутників для визначення точок земної поверхні і створювати таким чином геодезичні мережі з відповідними координатами їх пунктів. Теоретичними засадами методів космічної геодезії є практичний розв’язок основного рівняння космічної геодезії, записаного в такому вигляді. Нехай точка на земній поверхні Q і супутник в точці С, який знаходиться на орбіті, визначається в геоцентричній системі координат векторами:
З аналізу цього рівняння (1.1) бачимо що воно дає можливість визначити як координати точки земної поверхні Космічна геодезія є важливою частиною геодезичної науки оскільки дозволяє вирішувати не тільки перераховані задачі, а й виконувати зйомку земної поверхні з супутників і використовувати ці знімки для картографування. Системи координат В цій с-мі площину земного екватора приймають за координатну площину. Положення довільної точки М визначається двома координатами: географ. широта і географ. довгота. Широтою називається гострий кут утворений прямовисною лінією в точці спостер. М і площиною екватора. Довготою є двогранний кут при полюсі утворений площинами початкового меридіана і меридіана точки спостереження. Системи виміру часу.
Для фіксації одиниць часу встановлюють точки чи лінії за допомогою яких і фіксують ці одиниці, тому в залежності від вибору точок розрізняють різні системи часу. Відомо, що при фіксації зоряної доби як одиниці зоряного. часу використовують точку весняного рівнодення і меридіан точки спостереження. За добу точка весняного рівнодення буде два рази перетинати меридіан точки спостереження: у точках верхньої кульмінації і нижньої. Зоряною добою є проміжок часу між двома однойменними послідовними кульмінаціями точки весняного рівнодення на меридіані т. спостереження. За початок зоряної доби приймають момент нижньої кульмінації. Мірою зор. часу є годинний кут точки весняного рівнодення. Істинний час. Ця система виміру часу для фіксації одиниці часу використовують центр істинного сонця і меридіан точки спостереження. У своєму видимому русі сонце буде перетинати площину меридіана у двох точках(в. і н. кульмінації). Істинною добою називають проміжок часу між двома послідовними однойменними кульмінаціями центра істинного сонця на меридіані точки спостереження. За початок доби приймають точку нижньої кульмінації. Мірою істинного часу є величина годинного кута. Час, який фіксується за допомогою середнього екваторіального Сонця назив. середнім часом. Середньою добою є проміжок часу між двома послідовними та однойменними кульмінаціями сер. екватор. сонця на меридіані точки спостережень. Середнім екліптичним сонцем назив. фіктивну точку що рухається по екліптиці з рівномірною швидкістю, що = сер. швидк. руху реального сонця за рік. Сер. екваторіальним сонцем є фіктивна точка що рухається по екватору рівномірно зі швидкістю сер. екліпт. сонця. Періодичні зміни в періоді обертання пов’язані з сезонною циркуляцією мас атмосфери. В зимовий період атмосферні маси рухаються в напрямку протилежному до напрямку обертання Землі –гальмівний ефект; а у літній час - співпадає, тобто швид. обертання прискорюється. Ці фактори можуть змінювати період обертання, тому була введена система земного динамічного часу. Одиницею часу є одна ефемеридна секунда 1 сек=1 / 31556925 частина тропічного року. Тривалість тропічного року 365,2422 сер. діб.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.147.12 (0.016 с.) |

 ,
,  , приймемо що положення супутника відносно точки спостереження визначається вектором
, приймемо що положення супутника відносно точки спостереження визначається вектором  . Тоді з векторного трикутника
. Тоді з векторного трикутника  правомірним є рівняння:
правомірним є рівняння: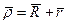 , (1.1)
, (1.1)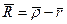 , (1.2)
, (1.2)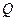 вектором
вектором  - зор. час
- зор. час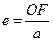 , (1.8)
, (1.8) – орбіта коло;
– орбіта коло; – парабола;
– парабола; – еліпс;
– еліпс; – гіпербола.
– гіпербола. – істина аномалія.
– істина аномалія.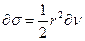

 повинна бути стала, звідси
повинна бути стала, звідси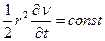 , (1.10)
, (1.10)
 також не повинно бути сталим.
також не повинно бути сталим.  , (1.11)
, (1.11) , (1.12)
, (1.12) є точка весняного рівнодення. Кут утворений в площині небесного горизонту напрямками на точку весняного рівнодення і на точку висхідного вузла називають довготою висхідного вузла орбіти. Довгота висхідного вузла завжди відраховується від напрямку на точку весняного рівнодення, проти ходу годинникової стрілки і до напрямку на висхідний вузол. Може приймати значення від 0 до 360.
є точка весняного рівнодення. Кут утворений в площині небесного горизонту напрямками на точку весняного рівнодення і на точку висхідного вузла називають довготою висхідного вузла орбіти. Довгота висхідного вузла завжди відраховується від напрямку на точку весняного рівнодення, проти ходу годинникової стрілки і до напрямку на висхідний вузол. Може приймати значення від 0 до 360. називається сферична відстань точки перігея від висхідного вузла орбіти відрахована по самій орбіті.
називається сферична відстань точки перігея від висхідного вузла орбіти відрахована по самій орбіті.
 , (1.13)
, (1.13) по орбіті пройшов за час t. Швидкість руху на цій ділянці буде максимальною Vmax. Середня швидкість на цій ділянці Vo<Vmax. Тому по орбіті в вигляді кола супутник за час t, рухаючись зі швидкістю Vo пройде дугу ПС". Кут утворений напрямком на точку перигея і напрямком на точку С`` називається середньою аномалією M.
по орбіті пройшов за час t. Швидкість руху на цій ділянці буде максимальною Vmax. Середня швидкість на цій ділянці Vo<Vmax. Тому по орбіті в вигляді кола супутник за час t, рухаючись зі швидкістю Vo пройде дугу ПС". Кут утворений напрямком на точку перигея і напрямком на точку С`` називається середньою аномалією M. , отримаємо:
, отримаємо:


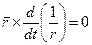
 , (1.16)
, (1.16)
 , (1.17)
, (1.17)
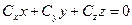 , (1.18)
, (1.18)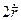 , отримаємо:
, отримаємо:
 , (1.19)
, (1.19)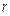 і
і  є направлені один по одному то, то косинус між ними дорівнює 1. праву частину вихідного рівняння перетворимо наступним чином:
є направлені один по одному то, то косинус між ними дорівнює 1. праву частину вихідного рівняння перетворимо наступним чином: , (1.20)
, (1.20)
 , (1.21)
, (1.21) потенціальну енергію супутника. Інтеграл енергії можна отримати і в такому вигляді:
потенціальну енергію супутника. Інтеграл енергії можна отримати і в такому вигляді: , (1.22)
, (1.22) , (1.23)
, (1.23) в (1.22) його вираз з (1.23)
в (1.22) його вираз з (1.23) , (1.24)
, (1.24)


 , тоді замінимо цим виразом праву частину
, тоді замінимо цим виразом праву частину , (1.31)
, (1.31)
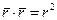
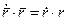
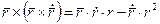

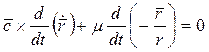

 , (1.32)
, (1.32)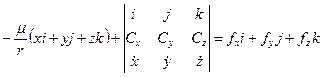 , (1.33)
, (1.33)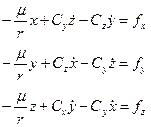 , (1.34)
, (1.34)
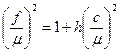
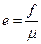 , (1.35)
, (1.35)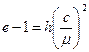
 знаючи диференціальні рівняння збуреного руху.
знаючи диференціальні рівняння збуреного руху.  , (1.54)
, (1.54) , а також координати x,y,z супутника в тій чи іншій точці реальної орбіти. Якщо для цієї ж точки на основі теорії незбуреного руху обчислити незбурені координати
, а також координати x,y,z супутника в тій чи іншій точці реальної орбіти. Якщо для цієї ж точки на основі теорії незбуреного руху обчислити незбурені координати 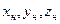 ,а також швидкості
,а також швидкості 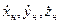 ,по відповідних напрямках координатних осей, то порівнюючи збурені і незбурені координати отримують значення збурень.
,по відповідних напрямках координатних осей, то порівнюючи збурені і незбурені координати отримують значення збурень. (1.55)
(1.55)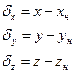 (1.56)
(1.56)



