
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Використання диференціальних формул руху супутника для визначення параметрів орбітиСодержание книги
Поиск на нашем сайте
Інтеграл Лапласа у векторній формі (1.32) помножимо скалярно на вектор
З отриманого виразу знайдемо:
Враховуючи (1.23) і (1.35) отримаємо:
Ця формула справедлива для випадку коли супутник знаходиться на осі апсид в точці перигею. У випадку довільного розміщення супутника на орбіті:
Отримаємо рівняння Кларо для незбуреного руху супутника по орбіті. Супутник знаходиться в т С і його положення визначається кутом істинної аномалії. Введемо локальну систему координат, центр якої сумістимо з центром орбіти т О. запишемо рівняння площини для даної орбіти
Розпишемо інтеграл площ в пристосуванні до даної координатної системи.
Або запишемо по координатах
Проаналізуємо систему рівнянь (1.39) виходячи із можливого значення координат супутника.
Запишемо координати
Підставимо ці значення в (1.40)
Замінимо в (1.42) r його виразом з (1.38)
Інтегруємо отриманий вираз
З другого закону Кєплера відомо, що істинна аномалія є величина, яка змінюється нерівномірно при русі супутника по орбіті, замінимо її іншою величиною, яка називається ексцентричною аномалією. Цю заміну робимо виходячи із залежності:
е – ексцентриситет E – ексцентрична аномалія Перетворимо цю формулу з метою визначення знаменника(1.43)
З тригонометрії відомо
Приведемо отриманий вираз до спільного знаменника і розкриємо дужки.
На основі (1.45) визначимо вираз для знаменника підінтегрального виразу:
Для визначення (1.39) диференціюємо (1.44)
Відомо, що
В отриманому виразі для заміни замість
Підставимо цей вираз в (1.47)
Підставляємо (1.48) і (1.46) в (1.43)
Інтегруємо отриманий вираз:
Зробимо перетворення лівої частини (1.49) виходячи з того, що
Відомо також
Введемо позначення Середній рух – Величина, що визначається формулою (1.50) характеризує середню швидкість супутника по орбіті у вигляді кола радіуса а.
Назвемо (1.51) середньою аномалією. Середня аномалія, кут відрахований від напрямку на точку перигею до супутника на коловій орбіті радіуса а в момент спостереження. З врахуванням (1.50) і (1.51) знайдемо:
Рівняння (1.52) е рівнянням Кєплера для незбуреного руху супутника по орбіті. Встановимо ще одну залежність між елементами незбуреної орбіти супутника. Формула (1.46) встановимо залежність між ексцентриситетом, істинною і ексцентричною аномалією. Відомо, що радіус вектор визначається:
Зробимо відповідні заміни в (1.46)
Збурений рух ШСЗ Рух супутника за законами Кеплера передбачає ідеальний випадок руху, при якому на супутник впливала би тільки сила тяжіння утворена Землею, як тілом правильної геометричної форми, або абсолютно твердим, або з правильним і незмінним розподілом мас. Для реальної Землі всі ці умови не виконуються, оскільки вона не має правильної геометричної форми, не має правильного розподілу мас, і крім того на супутник будуть діяти сили тяжіння, що утворюють інші небесні тіла, тому реальний рух супутника відбувається по реальних орбітах і такий рух називається збуреним, а орбіта-збуреною. Очевидно, що елементи орбіти супутника(реальної) і елементи, які характеризують положення супутника на реальній орбіті будуть відрізнятися від відповідних елементів незбуреної орбіти. Ці різниці називаються збуреннями відповідних елементів. Очевидну величину збурень можна визначити
В рівнянні (1.54) в правій частині диф. р-ня знаходиться прискорення ω по осях координат X,Y,Z. Ці прискорення і характеризують вплив різноманітних факторів на рух супутника. Безпосереднє інтегрування р-ня (1.54) неможливе, оскільки дуже багато різноманітних факторів впливає на збурення, тому розв’язок цих диф. рівнянь проводять приблизними методами, що дозволяють визначати швидкості
(1.55) і (1.56) дозволяють обчислювати відповідні збурення і через них визначити збурення відповідних елементів орбіти.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 278; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.170.65 (0.009 с.) |


 , (1.32)
, (1.32)






 , (1.23)
, (1.23) , (1.37)
, (1.37) , (1.38)
, (1.38)
 , (1.39)
, (1.39) , (1.40)
, (1.40) через радіус вектор і істинну аномалію
через радіус вектор і істинну аномалію , (1.41)
, (1.41)


 , (1.42)
, (1.42)
 , (1.43)
, (1.43) , (1.44)
, (1.44)






 , (1.45)
, (1.45)
 , (1.46)
, (1.46)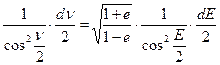

 підставимо (1.44)
підставимо (1.44)


 , (1.48)
, (1.48)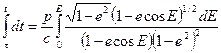

 , (1.49)
, (1.49)



 , (1.50)
, (1.50) , (1.51)
, (1.51) , (1.52)
, (1.52)


 , (1.53)
, (1.53) знаючи диференціальні рівняння збуреного руху.
знаючи диференціальні рівняння збуреного руху.  , (1.54)
, (1.54) , а також координати x,y,z супутника в тій чи іншій точці реальної орбіти. Якщо для цієї ж точки на основі теорії незбуреного руху обчислити незбурені координати
, а також координати x,y,z супутника в тій чи іншій точці реальної орбіти. Якщо для цієї ж точки на основі теорії незбуреного руху обчислити незбурені координати 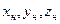 ,а також швидкості
,а також швидкості 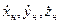 ,по відповідних напрямках координатних осей, то порівнюючи збурені і незбурені координати отримують значення збурень.
,по відповідних напрямках координатних осей, то порівнюючи збурені і незбурені координати отримують значення збурень. (1.55)
(1.55)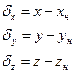 (1.56)
(1.56)


